4.Синтез корректирующего устройства.

4.1.Синтез корректирующего устройства методом Соколова.

На первом этапе определяется разность порядков полиномов знаменателя (n₁) и числителя (m₁) передаточной функции замкнутой нескорректированной системы

(n₁-m₁).

n₁-m₁=4-0=4

ν=1

На втором этапе формируется желаемая передаточная функция замкнутой системы, удовлетворяющая заданным требованиям к качеству синтезируемой системы на основе нормированных передаточных функций.

Требования к синтезируемой системе:

^зад=20 %;

=0,25, с

При формировании желаемой передаточной функции

степени m и n соответственно полиномов B(S) и A(S) выбирают,

исходя из следующих соотношений:

m=ν-1=1-1=0,

n=(n₁-m₁)+ν-l=4+1-1=4,

Нормированная передаточная функция Ф_н(р) будет иметь те же порядки n и m. Коэффициенты этой функции определяют из соответствующей Таблицы А.1 Приложение. Минимальное время регулирования в приложении.

По переходной характеристике нормированной функции (рис.4.1) определяют время переходного процесса τ_н.

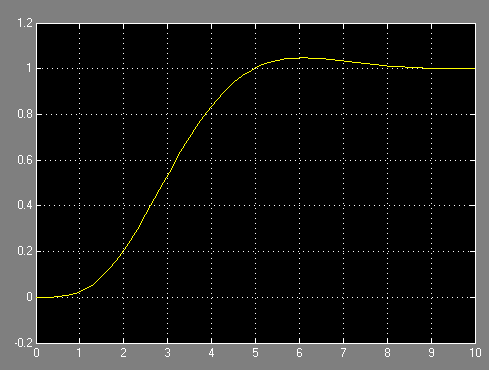
Рис.4.1

τ_н=4.58 c.

Переход от Ф_н(р) к Ф_ж(s) производится на основании теоремы масштабов преобразования Лапласа с использованием следующего соотношения

p=sz,

Желаемую передаточную функцию можно получить, из равенства

Ф_ж(s)=Ф_н(sz)

Структурная схема скорректированной системы изображена на рис.4.2. Н определить передаточную функцию корректирующего устройства (КУ).

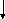f(t)

W₂(s)

W₁(s)

g(t) x(t)

W_ку(s)

рис.4.2

Для упрощения вычислений вначале нужно записать эквивалентную передаточную функцию объекта управления и КУ.

Передаточная функция скорректированной системы запишется как

;

;

;

.

Откуда можно выразить передаточную функцию корректирующего устройства

;

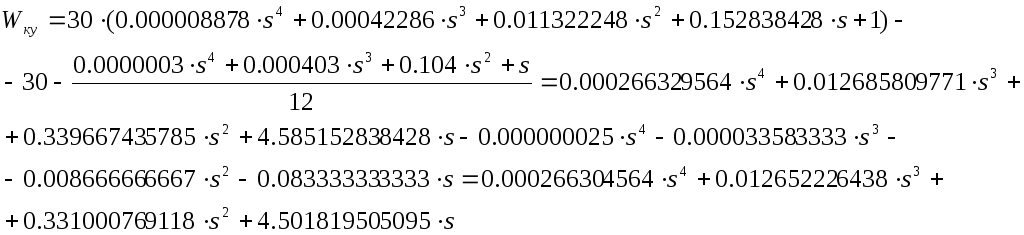
При подстановке исходных данных выражение примет вид

.

4.2.Анализ качества скорректированной сау.

Переходная характеристика скорректированной системы изображена на рис.4.3

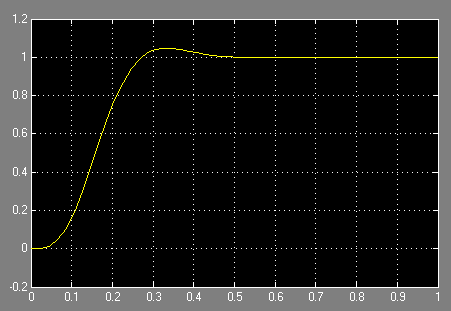
Рис.4.3

Время регулирования и перерегулирование численно равны

t_рег=0.25 c  =4.23 %.

Полученные значения удовлетворяют требованиям к синтезируемой системе.

Оценка запасов устойчивости по модулю и по фазе путем построения ЛАХ и ЛФХ (рис.4.4)

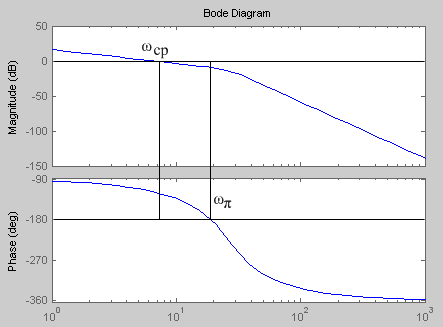
рис.4.4

По рис.4.5 определяют запасы устойчивости по модулю и по фазе, а так же ω_π и ω_ср

Система устойчива так как .

Определение коэффициентов ошибок.

С помощью MatLab можно определить значение коэффициентов ошибок:

;

;

.

Полученные коэффициенты ошибок отличаются от заданных, потому что в качестве главного критерия при формировании передаточной функции желаемой системы выступало минимальное время регулирования.

4.3.D-разбиение в области одного параметра.

Метод D-разбиения заключается в определении допустимой области изменения одного или нескольких параметров, при условии, что система не потеряет свою устойчивость.

Во-первых, необходимо записать передаточную функцию замкнутой системы и характеристичное уравнение

;

;

.

Передаточная функция скорректированной системы в общем виде

.

Характеристическое уравнение имеет вид

.

Во-вторых, необходимо выразить через остальные параметры

;

.

При s→jω выражение примет вид

После постановки выпажени примет вид

.

Кривая D-разбиения в области параметра изображена на рис.4.5

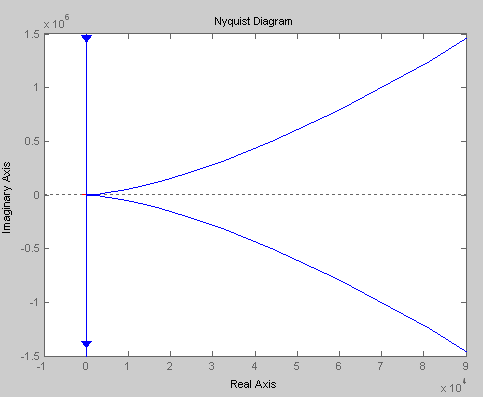
Рис.4.5

Так как параметр должен принимать только действительные значения, то в полученной области необходимо выбрать только те значения, при которых Im()=0.

Область значений:

Необходимо проверить, будет ли являться данный диапазон областью устойчивости, приняв равным любому значению из данного диапазона.

Пусть . Передаточная функция замкнутой системы примет вид:

Требуется проверить устойчивость данной системы по любому из критериев устойчивости. На рис.4.6 изображен годограф скорректированной системы в разомкнутом виде.

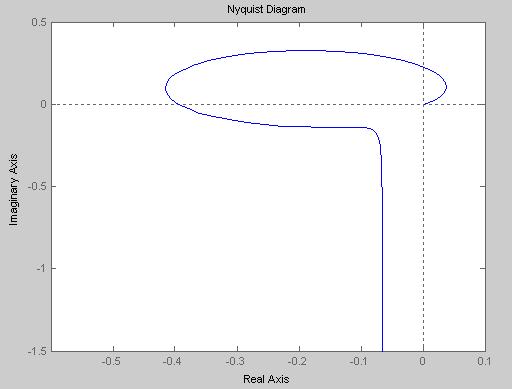
Рис.4.6

Годограф не охватывает точку (–1; j0). Система устойчива по Найквисту.