
- •Часть 1. Методологические аспекты моделирования
- •Часть 3. О методике построения математических моделей
- •Часть 4. Экспертиза в системном анализе
- •Объект и предмет исследования
- •Часть 1. Методологические аспекты моделирования
- •Понятие моделирования
- •1.2. Обобщенный процесс моделирования
- •1.3. Математические модели
- •Часть 2. Элементы теории систем
- •2.1. Система и ее компоненты
- •2.2. Строение системы
- •2.2.1. Связи в системе
- •2.2.2. Структура системы
- •2.2.3. Пространственные и временные связи
- •2.2.4. Описание системы
- •2.3. Классификация систем
- •2.3.1. Понятие классификации
- •2.3.2. Основные методы классификации
- •Иерархическая схема классификации.
- •Классификация систем по степени структурированности.
- •2.4. Системные принципы
- •2.4. Основы системного анализа
- •2.4.1. Понятие системного анализа
- •2.4.2. Этап постановки проблемы
- •2.4.3. Содержание системного анализа
- •Часть 3. О методике построения математических моделей
- •3.1. Анализ задачи
- •3.2. Этап формирования математической модели
- •3.3. Классификация математических моделей
- •3.4. Модель черного ящика
- •3.5.Теоретико-множественная модель
- •3.6. Типовые математические схемы
- •Непрерывно-детерминированные модели (d - схемы).
- •3.7. Пример построения динамической модели
- •3.8. Метод статистических испытаний (метод Монте – Карло)
- •3.9. Имитационное моделирование
- •3.10.1. Понятие нечеткого множества
- •3.10. Операции над нечеткими множествами.
- •3.10.3. Нечеткие отношения
- •3.10.4. Нечеткие и лингвистические переменные.
- •3.10.5. О построении функций принадлежности
- •3.10.6. Элементы нечетких алгоритмов
- •Стандартные графики функции принадлежности
- •Часть 4. Экспертиза в системном анализе
- •4.1. Методы проведения экспертизы в системном анализе
- •4.1.1. Основные задачи экспертизы в системном анализе
- •4.1.2. Методы коллективной генерации идей
- •4.1.3. Структуризация систем
- •4.1.4. Морфологические методы
- •4.2. Измерение
- •4.2.1. Понятие измерения
- •4.2.2. Шкалы измерений числовых показателей.
- •4.2.3. Шкала измерений нечисловых показателей
- •4.2.4. Сравнительный анализ шкал
- •4.3. Обработка экспертных измерений
- •2.4.1. Ранжировка и оценка в баллах
- •2.4.2. Исследование зависимости показателей качества, измеряемых в нечисловых шкалах
- •4.4.3. Оценка степени согласованности порядковых показателей
- •4.4.4. Проверка степени несогласованности и безразличия экспертов
- •Заключение
- •Библиография
- •Живицкая е.Н., о.П. Едемская. Системный анализ и проектирование информационных систем: Учебно-метод. Пособие. / Мн.: бгуир, 2005.
3.5.Теоретико-множественная модель
Модель «черного ящика» позволяет решать достаточно широкий спектр задач, требующих ответа на вопрос о свойствах объекта-оригинала в целом. Внутренние же причины, обусловливающие эти свойства, модели такого типа могут описывать лишь косвенно. Для поиска же ответов на вопросы как устроена система, как протекают ее внутренние процессы и почему она функционирует именно так, а не иначе и, соответственно, что и как для этого нужно делать, требуются иные модели. Одним из типов модели, которые позволяют судить о том, как устроена система, является модель ее структуры.
Моделями структуры называют формализованное описание составляющих систему компонентов и фиксированных между ними отношений. Наиболее распространенной формой таких моделей широко применяемые в повседневной деятельности являются различные графические схемы, однако они практически не подходят для формализованных преобразований и здесь не рассматриваются. К моделям структуры можно отнести совокупности связанных между собой моделей черного ящика. Кстати, строго говоря, модель "черного ящика" – в некоторой степени уже является структурированной моделью: ведь для ее построения обычно используются сведения о некоторых связях рассматриваемой системы со средой, по крайней мере то, что относится данная связь к числу входов или является выходом.
Для описания структуры системы часто используются так называемые теоретико-множественные модели. Модель называется теоретико-множественной, если в описании объекта моделирования, как системы, используются только множества и заданные на этих множествах отношения.
Строго говоря, все способы задания формального описания не более чем отношения. Однако когда говорят о теоретико-множественной модели, то имеют ввиду предельно общий вид модели
![]() ,
,
где
![]() - базовое множество модели,
- базовое множество модели,
![]() - множество заданных на
- множество заданных на
![]() отношений.
отношений.
При моделировании в целом и при построении теоретико-множественных моделей именно отношениям отводится важнейшее место, поскольку всякое отношение можно рассматривать, как описание состояний объектов или взаимодействие. В частности можно провести следующие параллели между вербальным описанием объекта рассмотрения и его теоретико-множественной модели. Действительно, каждое высказывание содержит две основные лингвистические категории: термы (денотанты) и функтуры. В модели термы используются для обозначения объектов, а функторы – для обозначения отношений между ними.
Пусть
![]() некоторое множество. Соответствие
частного вида
некоторое множество. Соответствие
частного вида
![]() между множеством
между множеством
![]() и этим же множеством
и этим же множеством
![]() обычно называют бинарным отношением
на множестве
обычно называют бинарным отношением
на множестве
![]() .
Если
.
Если
![]() ,
то говорят, что элемент
,
то говорят, что элемент
![]() находится в отношении
находится в отношении
![]() с элементом
с элементом
![]() ,
и этот факт обычно обозначают через
,
и этот факт обычно обозначают через
![]() .
В общем случае можно рассматривать
отношения между
.
В общем случае можно рассматривать
отношения между
![]() элементами, т.е.
элементами, т.е.
![]() -местные
отношения
-местные
отношения
![]() 1.
1.
Поскольку понятие отношение используется при математическом моделировании в качестве базового, то полезно напомнить следующие моменты теории отношений. Определяющими атрибутами любого отношения являются 1:
-
свойство, по которому определяется отношение рассматриваемых элементов;
-
размерность, или, другими словами, мера данного свойства, определяющая соответствующую единицу измерения;
-
область значений, представляющая собой базовое множество данного свойства;
-
имя отношения, которое является символическим ярлыком его сущности. (Сущность есть концентрированное выражение свойств некоторого объекта);
-
время, к которому относится отношение (настоящее, прошедшее или будущее);
-
формула, представляющая собой конструкцию из символов определенного языка, отражающую сущность отношения;
Всеобщими свойствами отношений являются:
-
истинность – характеристика реальности отношения в определенных условиях; отношение, как субъективное отражение объективной реальности, может быть истинным, ложным или неопределенным, мерой истинности, как правило, служит вероятность;
-
местность, по количеству аргументов отношение может быть одноместным, двухместным и так далее, вообще говоря, n-местным;
-
сущность, как концентрированное выражение совокупности основных логических свойств отношения: симметричности, транзитивности, рефлексивности, антисимметричности и антирефлексивности;
-
предметность, устанавливающая связь отношения с конкретными свойствами конкретных элементов.
При рассмотрении сложной системы с многоуровневой структурой число элементов самой модели становится весьма большим, их перечисление ненаглядным, трудно воспринимаемым и анализируемым. Такого рода трудности обычно преодолевают путем упрощения модели за счет более узкого, конкретного представления объекта.
Теоретико-множественное описание представляет собой универсальную модель, поскольку может быть применена к весьма широкому классу систем. Более того, можно признать целесообразным построение теоретико-множественной модели в качестве первоначального формального описания объекта моделирования. Именно в таком виде удобно формализовать концептуальное описание системы, поскольку концептуальная модель в конечно счете и есть описание определенной структуры взаимосвязанных понятий и отношений между ними. Теоретико-множественные модели часто выступают основой для построения так называемых типовых моделей.
В качестве примера теоретико-множественной модели приведем модель построения иерархических онтологий основанных на отношении наследования атрибутов понятий данной предметной области 1 .
Пусть имеется некоторая онтология, включающая известное количество концептов, между которыми установлено отношение наследования. Каждый концепт считается описанным, т.е. известен состав, описывающих его атрибутов.
Эксперт, ознакомившись с существующей онтологией (со списком концептов и атрибутов) предполагает включить в состав онтологии новый концепт. Для этого он формирует полный с его точки зрения набор атрибутов вводимого концепта и вводит его в компьютер. Далее компьютер в автоматическом режиме находит место вводимого концепта в онтологии и фиксирует его там.
Ставится задача построения модели автоматического размещения в существующую онтологию нового концепта при условии сохранения корректности ее структуры.
Моделью онтологии назовем следующий кортеж
![]() ,
,
где
![]() - множество концептов, образующих
онтологию
- множество концептов, образующих
онтологию
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() ;
;
 -
множество атрибутов концепта
-
множество атрибутов концепта
![]() (
(![]() - количество атрибутов, описывающих
данный концепт);
- количество атрибутов, описывающих
данный концепт);
![]() -
отношение непосредственного наследования.
Отношение
-
отношение непосредственного наследования.
Отношение
![]() удобно задавать матрицей размером
удобно задавать матрицей размером
![]() :
если концепт
:
если концепт
![]() в данной онтологии непосредственно
наследует концепту
в данной онтологии непосредственно
наследует концепту
![]() ,
т.е.
,
т.е.
![]() ,
то элемент
,
то элемент
![]() ,
в противном случае, если
,
в противном случае, если
![]() ,
то
,
то
![]() Нахождение двух концептов в отношении
непосредственного наследования иерархии
онтологии свидетельствует о том, что
между ними нет ни одного иного концепта
Нахождение двух концептов в отношении
непосредственного наследования иерархии
онтологии свидетельствует о том, что
между ними нет ни одного иного концепта
![]()
Наряду
с непосредственным наследованием
(наследование родителям) введем понятие
опосредованного наследования (наследование
прародителям). Достаточным условием
опосредованного наследования (или
просто наследования) концепта
![]() концепту
концепту
![]() является условие
является условие
![]() .
Заметим, что для непосредственного
наследования это условие является лишь
необходимым
.
Заметим, что для непосредственного
наследования это условие является лишь
необходимым
![]() .
Обратное следование в общем случае не
имеет места. В представленной на рис.3.2.
структуре, например, концепт
.
Обратное следование в общем случае не
имеет места. В представленной на рис.3.2.
структуре, например, концепт
![]() непосредственно наследует
непосредственно наследует
![]() ,
а концепт
,
а концепт
![]() наследует
наследует
![]() лишь опосредовано, через концепт
лишь опосредовано, через концепт
![]() .
Содержательно наследование означает,
что наследующий концепт содержит все
атрибуты своих «родителей» и «прародителей»,
а также еще один или несколько «лично
своих атрибутов».
.
Содержательно наследование означает,
что наследующий концепт содержит все
атрибуты своих «родителей» и «прародителей»,
а также еще один или несколько «лично
своих атрибутов».

Рис.3.2. Пример структуры онтологии
Примечание.
Если выполнено условие
![]() ,
то концепты
,
то концепты
![]() и
и
![]() будем считать концептами-синонимами.
Будем считать, что введение концепта-синонима
не меняет онтологию. Вместе с тем для
фиксации наличий у некоторых концептов
данной онтологии синонимов может быть
сформирована специальная матрица,
используемая исключительно для
информирования экспертов.
будем считать концептами-синонимами.
Будем считать, что введение концепта-синонима
не меняет онтологию. Вместе с тем для
фиксации наличий у некоторых концептов
данной онтологии синонимов может быть
сформирована специальная матрица,
используемая исключительно для
информирования экспертов.
В
онтологии могут присутствовать так
называемые «обобщающие концепты».
Концепт
![]() называется обобщающим по отношению к
концептам
называется обобщающим по отношению к
концептам
![]() и
и
![]() ,
если
,
если
![]() .
В онтологии, представленной на рис.3.2.
концепт
.
В онтологии, представленной на рис.3.2.
концепт
![]() является обобщающим для концептов
является обобщающим для концептов
![]() и
и
![]() .
Очевидно, что концепт может быть
обобщением произвольного числа концептов.
.
Очевидно, что концепт может быть
обобщением произвольного числа концептов.
Следует
обратить внимание на следующее важное
обстоятельство. Онтология считается
построенной корректно, если в ней
отсутствуют структуры ложного обобщения.
Содержательно обобщение является
ложным, если концепт непосредственно
наследует двум концептам (или большему
их числу), но один (или несколько) из них
одновременно является (возможно и
опосредованным) наследником другого.
Условие отсутствия в онтологии ложных
обобщений следующее:
![]()
Данную ситуацию демонстрирует рис.3.3.
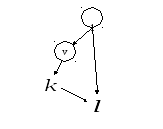
Рис.3.3. Пример ложной структуры обобщения.
Основная идея предлагаемого метода построения онтологии изложенная в работе 1 заключается в том, чтобы для вводимого концепта найти тот концепт в существующей онтологии, которому он непосредственно наследует при отсутствии ложных обобщений.
Опишем
процедуру автоматического наращивания
онтологии. Вначале должен быть реализован
стартовый, так называемый нулевой шаг
– сформирование элементарной онтологии.
Корневым называем такой концепт, атрибуты
которого наследуют все концепты данной
онтологии. Для формирования корневого
концепта
![]() вводится его имя и список присущих ему
атрибутов. В качестве первого концепта
целесообразно (хотя и не обязательно)
выбирать наиболее общее для данной
предметной области понятие. Следующий
вводимый концепт
вводится его имя и список присущих ему
атрибутов. В качестве первого концепта
целесообразно (хотя и не обязательно)
выбирать наиболее общее для данной
предметной области понятие. Следующий
вводимый концепт
![]() ,
если он наследует корневому концепту,
становится непосредственно ему следующим
(
,
если он наследует корневому концепту,
становится непосредственно ему следующим
(![]() ).
В противном случае наоборот, вводимый
концепт становится корневым, а корневой
ему непосредственно наследующим. В
обоих случаях элементарная онтология
построена.
).
В противном случае наоборот, вводимый
концепт становится корневым, а корневой
ему непосредственно наследующим. В
обоих случаях элементарная онтология
построена.
Все
последующие шаги есть повторение
процедуры добавления в построенную
онтологию очередного концепта. Пусть
эксперт, желающий ввести в существующую
онтологию новый концепт, присвоил
вводимому концепту имя
![]() ,
а также сформировал множество его
атрибутов
,
а также сформировал множество его
атрибутов
![]() .
После введения этих сведений все
остальные операции по наращиванию
онтологии за счет введения в нее концепта
.
После введения этих сведений все
остальные операции по наращиванию
онтологии за счет введения в нее концепта
![]() совершаются автоматически.
совершаются автоматически.
Для
существующей онтологии всегда сформирован
упорядоченный (по мере поступления всех
включенных в онтологию концептов) полный
набор ее атрибутов
![]() :
:
![]()
Эксперту
предлагается указать из него все атрибуты
характерные, по его мнению, для вводимого
концепта и добавить, если он считает
необходимым, новые, т.е. сформировать
множество атрибутов вводимого концепта
 .
.
Заметим,
формируя
![]() ,
эксперт вводит в онтологию новые знания.
Следующий этап – определение места для
нового концепта в онтологии и внесение
в нее всех соответствующих изменений
выполняется без участия людей.
,
эксперт вводит в онтологию новые знания.
Следующий этап – определение места для
нового концепта в онтологии и внесение
в нее всех соответствующих изменений
выполняется без участия людей.
Суть поиска места установки вводимого концепта заключается в поиске всех потенциальных его родителей и выбора из них только тех, которые совместно с вводимым концептом не образуют ложных обобщений.
Процедуру
поиска целесообразно начинать с корневого
концепта, поскольку особенностью
корневого концепта является то, что его
атрибуты (по определению) наследуются
всеми иными концептами онтологии. Это
касается и вводимого концепта, однако
требуется проверка того факта, что может
вводиться более общий концепт, чем
находящийся в онтологии. Если существующий
в онтологии корневой концепт наследует
вводимому концепту, т.е.
![]() ,
то после тщательной проверки вводимого
множества атрибутов
,
то после тщательной проверки вводимого
множества атрибутов
![]() (рекомендуемой
эксперту системой интерпретации) в
онтологии производится смена корневого
концепта, им становится вводимый концепт.
(рекомендуемой
эксперту системой интерпретации) в
онтологии производится смена корневого
концепта, им становится вводимый концепт.
В
противном случае переходят к общей
части процедуры. Из корневого концепта
и непосредственно наследующих ему
концептов для вводимого концепта
формируется множество потенциальных
концептов-родителей
 таких, что
таких, что
 .
Корневой концепт
.
Корневой концепт
![]() безусловно вводится в формируемое в
процессе процедуры отношение
безусловно вводится в формируемое в
процессе процедуры отношение
![]() (его элементы определяют потенциально
возможные места размещения вводимого
концепта):
(его элементы определяют потенциально
возможные места размещения вводимого
концепта):
![]() ,
т.е.
,
т.е.
![]() .
.
Опишем последующие шаги предлагаемой процедуры.
1.
Организуется просмотр потенциальных
концептов-родителей. Если
![]() (все потенциальные концепты-родители
рассмотрены), то переходят к п.5. Иначе
к п.2.
(все потенциальные концепты-родители
рассмотрены), то переходят к п.5. Иначе
к п.2.
2.
Из
![]() выбирают
следующий по порядку элемент. Пусть из
выбирают
следующий по порядку элемент. Пусть из
![]() выбран концепт
выбран концепт
![]() |
| .
Тогда возможны три варианта:
.
Тогда возможны три варианта:
2.1.
![]() .
В этом случае концепт
.
В этом случае концепт
![]() и все его наследники признаются не
перспективными и
и все его наследники признаются не
перспективными и
![]() исключается из множества
исключается из множества
![]() (
(![]() )
(заметим, что данное обстоятельство
свидетельствует о том, что данный
алгоритм «быстрее», чем полный перебор).
Для выбора следующего кандидата переходят
к п.1.
)
(заметим, что данное обстоятельство
свидетельствует о том, что данный
алгоритм «быстрее», чем полный перебор).
Для выбора следующего кандидата переходят
к п.1.
2.2.
![]() .
Это тот случай, когда вводимый концепт
должен быть вставлен между
.
Это тот случай, когда вводимый концепт
должен быть вставлен между
![]() и
и
![]() ,
где
,
где
![]() .
В этом случае концепт
.
В этом случае концепт
![]() и все его наследники признаются не
перспективными и
и все его наследники признаются не
перспективными и
![]() исключается из множества
исключается из множества
![]() (
(![]() )
(заметим, что данное обстоятельство
свидетельствует о том, что данный
алгоритм «быстрее», чем полный перебор).
Существовавшее в онтологии отношение
)
(заметим, что данное обстоятельство
свидетельствует о том, что данный
алгоритм «быстрее», чем полный перебор).
Существовавшее в онтологии отношение
![]() исключается, т.е.
исключается, т.е.
![]() и водятся новые два отношения
и водятся новые два отношения
![]() и
и
![]() ,
,
![]() и
и
![]() .
На рис.3.4. иллюстрируется ситуация, когда
в онтологию (см. Рис.3.2.) включен концепт
.
На рис.3.4. иллюстрируется ситуация, когда
в онтологию (см. Рис.3.2.) включен концепт
![]() .
Далее необходимо проверить, является
ли введенный концепт обобщенным. Для
этого процедура просто должна быть
продолжена, переходят к п.1.
.
Далее необходимо проверить, является
ли введенный концепт обобщенным. Для
этого процедура просто должна быть
продолжена, переходят к п.1.
2.3.
![]() .
Это означает, что
.
Это означает, что
![]() наследует
наследует
![]() .
Вводим в множество
.
Вводим в множество
![]() новый элемент:
новый элемент:
![]() ,
т.е.
,
т.е.
![]() (зафиксировано потенциальное место для
вводимого концепта) и
(зафиксировано потенциальное место для
вводимого концепта) и
![]() исключается из множества
исключается из множества
![]() (
(![]() ).
Очевидно, что в таком случае корневой
концепт также исключается из множества
).
Очевидно, что в таком случае корневой
концепт также исключается из множества
![]() (
(![]() )
и, что важно, из множества
)
и, что важно, из множества
![]()
![]() .
.
3.
Из потенциальных мест размещения
вводимого концепта (т.е.
![]() )
исключают, если таковой имеется, менее
перспективный концепт
)
исключают, если таковой имеется, менее
перспективный концепт
![]() ,
а именно:
,
а именно:
![]() ,
т.е.
,
т.е.
![]()
4.
Для
![]() формируется множество
формируется множество
![]() - множество непосредственно наследуемых
ему концептов
- множество непосредственно наследуемых
ему концептов
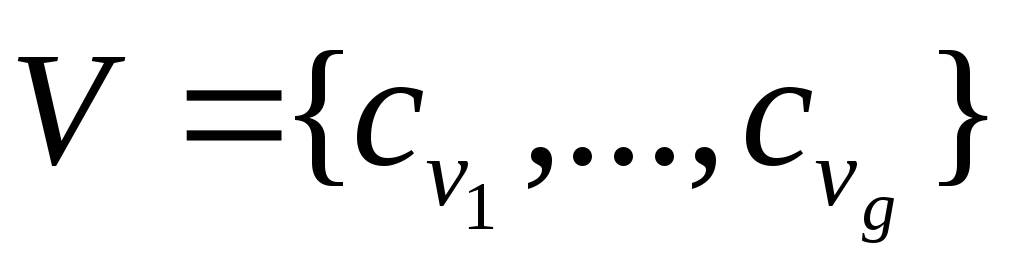 таких, что
таких, что
![]() .
Множество
.
Множество
![]() объединяют с множеством
объединяют с множеством
![]() :
:
![]() и переходят к п.1.
и переходят к п.1.
5.
Место для включения вводимого концепта
найдено (![]() )
и он включаться в состав онтологии. В
том случае, если найдено лишь одно
потенциальное место (
)
и он включаться в состав онтологии. В
том случае, если найдено лишь одно
потенциальное место (![]() ),
то:
),
то:
![]() .
.
Если
же в множестве временно образованного
отношения
![]() находится более одного элемента, то
соответствующий ему концепт онтологии
является обобщением. Тогда
находится более одного элемента, то
соответствующий ему концепт онтологии
является обобщением. Тогда
![]() ,
т.е.
,
т.е.
![]()

Рис.3.4. Иллюстрация
включения в онтологию нового концепта
![]() путем разрыва ранее существовавшего
отношения.
путем разрыва ранее существовавшего
отношения.
Эта
модель, ориентированная на системы
семантически-ориентированного доступа
может
быть представлена кортежем
![]() ,
состоящим из множества понятий
,
состоящим из множества понятий
![]() ,
множества атрибутов
,
множества атрибутов
![]() и заданного на множестве понятий
отношения непосредственного наследования
и заданного на множестве понятий
отношения непосредственного наследования
![]() таких, что:
таких, что:
-
 -
множество образующих онтологию
-
множество образующих онтологию
 понятий, где
понятий, где
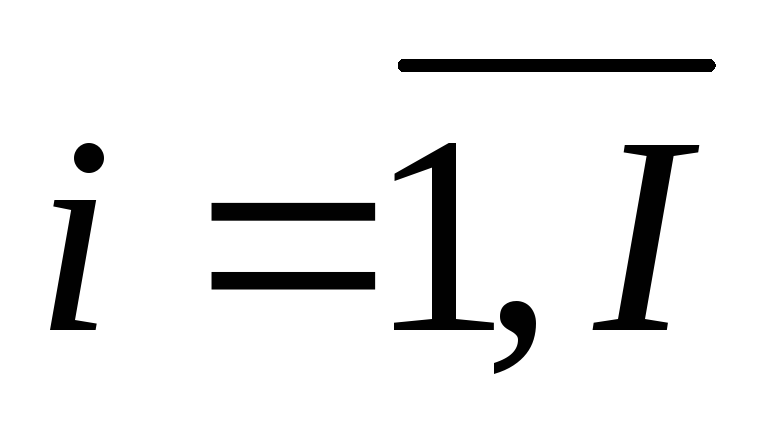 ,
,
 ;
; -
 -
множество атрибутов в онтологии
-
множество атрибутов в онтологии
 ,
где
,
где
 - совокупность атрибутов понятия
- совокупность атрибутов понятия
 ;
; -
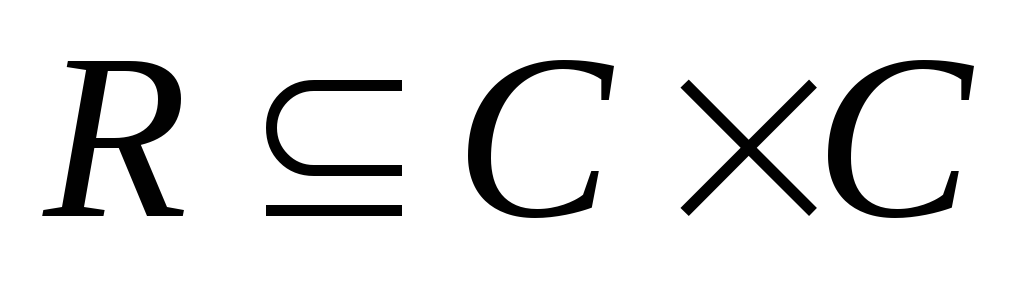 -
отношение непосредственного наследования,
которое задано матрицей размером
-
отношение непосредственного наследования,
которое задано матрицей размером
 такой, что
такой, что
 ,
если
,
если
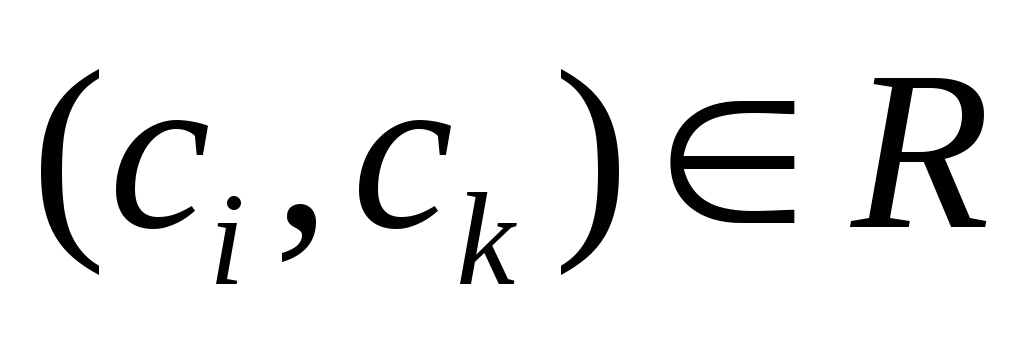 (
( )
и
)
и
 ,
если
,
если
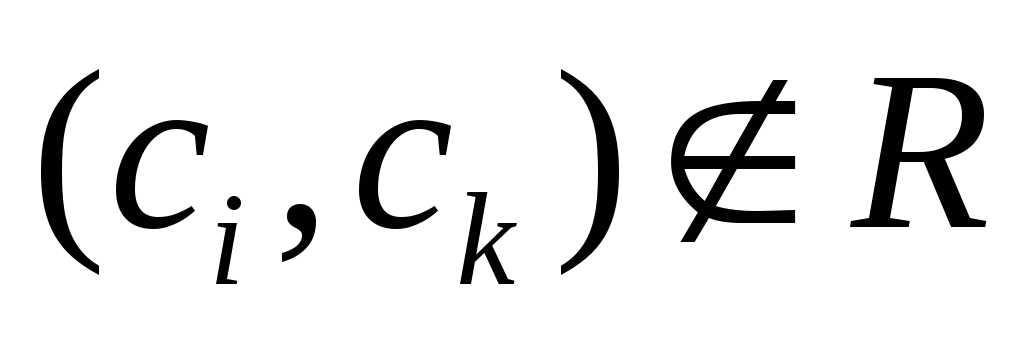 .
Причем дочернее понятие
.
Причем дочернее понятие
 непосредственно наследует родительскому
понятию
непосредственно наследует родительскому
понятию
 ,
если
,
если
 .
.
