
- •Методичні вказівки та завдання
- •1 Лабораторна робота № 1 тема: Методи розв’язання алгебраїчних і трансцендентних рівнянь
- •1.1 Відділення числового проміжку, у якому міститься один корінь рівняння
- •1.1.1 Відділення кореня графічно (перший спосіб)
- •1.1.2 Другий спосіб відділення кореня
- •1.2.1 Метод половинного ділення (метод бісекцій)
- •1.2.2 Метод хорд (метод пропорційних чисел)
- •1.2.3 Метод Ньютона (метод дотичних)
- •1.2.4 Використання пакету аналізу „что - если” Excel
- •1.3 Індивідуальні завдання
- •1.4 Приклади виконання лабораторної роботи
- •Тема: Методи розв’язання систем нелінійних рівнянь
- •2.3 Індивідуальні завдання
- •2.4 Приклади виконання лабораторної роботи
- •3 Лабораторна робота № 3 тема: Обчислення інтегралів
- •3.1 Теоретичні відомості
- •3.2 Індивідуальні завдання
- •3.3 Приклади виконання лабораторної роботи
- •4 Лабораторна робота №4 тема: Наближення (інтерполяція) функцій
- •4.1 Теоретичні відомості
- •4.2 Індивідуальні завдання
- •4.3 Приклади виконання лабораторної роботи
- •5 Лабораторна робота №5 тема: Апроксимація даних (емпіричні формули)
- •5.1 Теоретичні відомості
- •5.1.1 Визначення параметрів емпіричних формул по способу найменших квадратів у випадку лінійної залежності
- •5.1.2 Визначення параметрів емпіричних формул по способу найменших квадратів у випадку нелінійної залежності
- •5.2 Індивідуальні завдання
- •5.3 Приклад виконання лабораторної роботи
- •6 Лабораторна робота № 6 тема: Наближені методи розв’язку звичайних диференційних рівнянь
- •6.1. Теоретичні відомості
- •6.2 Індивідуальні завдання
- •8 Вимоги до оформлення лабораторної роботи
- •8.1 Додаток а
- •Запорізький національний технічний університет
3.2 Індивідуальні завдання
Для кожного варіанту:
1) обчислити інтеграл по формулі прямокутників з точністю ε = 0,01 ;
2) по формулі парабол обчислити інтеграл, уточнювання провести згідно формулі Річардсона.
3.2.1
1)
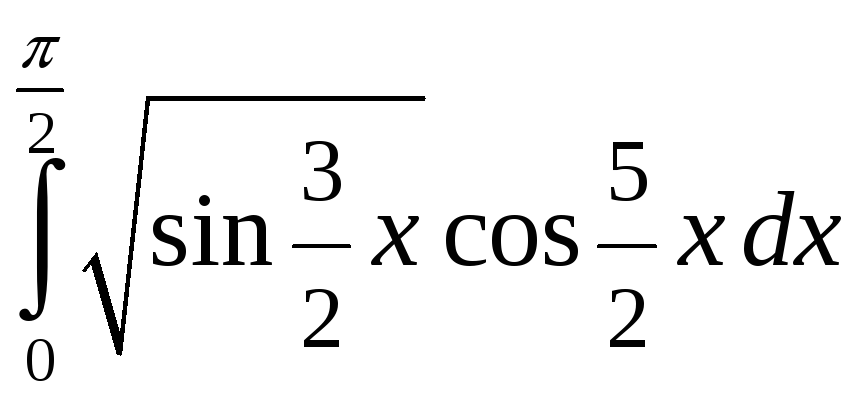 ;
2)
;
2)
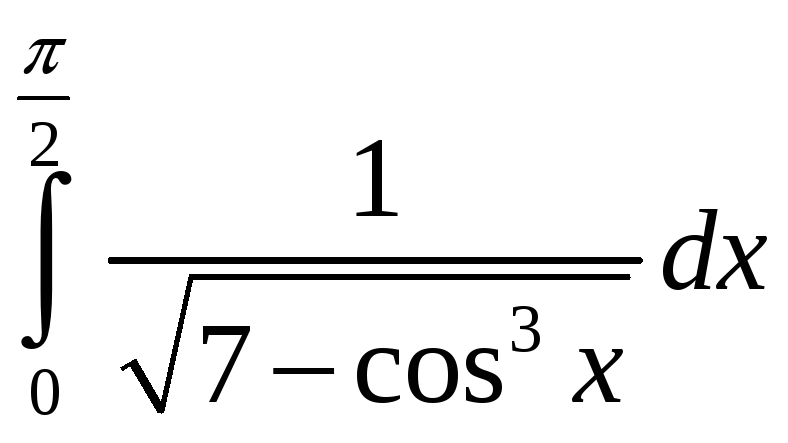 .
.
3.2.2
1)
![]() ;
2)
;
2)
![]() .
.
3.2.3
1)
![]() ;
2)
;
2)
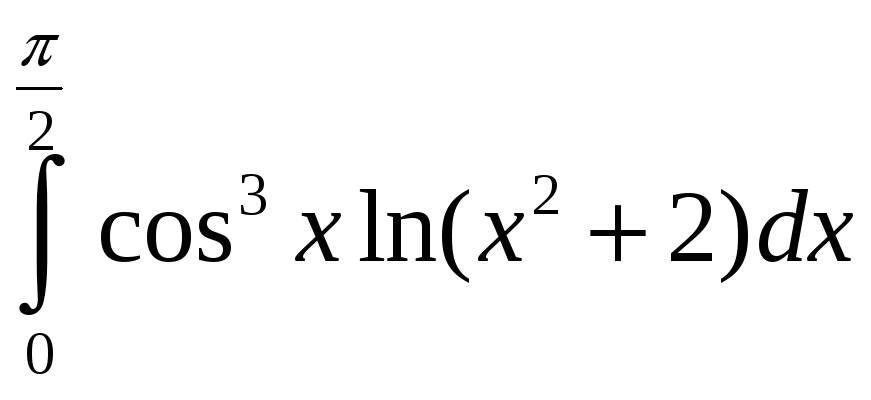 .
.
3.2.4
1)
![]() ;
2)
;
2)
 .
.
3.2.5
1)
![]() ;
2)
;
2)
![]() .
.
3.2.6
1)
![]() ;
2)
;
2)
![]() .
.
3.2.7
1)
![]() ;
2)
;
2)
![]() .
.
3.2.8
1)
![]() ;
2)
;
2)
 .
.
3.2.9
1)
![]() ;
2)
;
2)
![]() .
.
3.2.10
1)
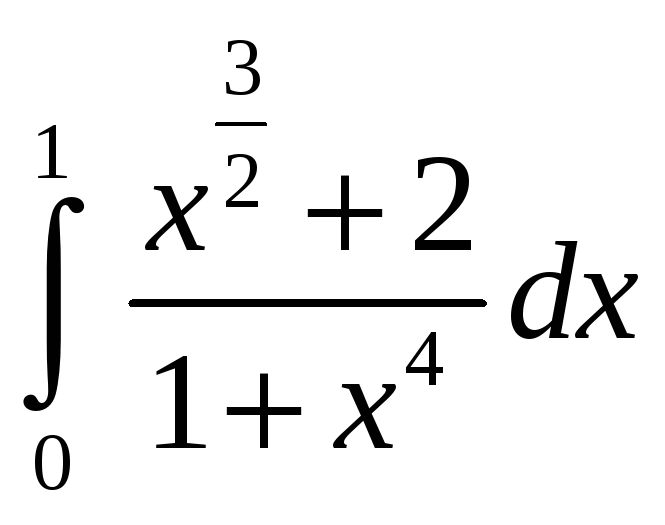 ;
2)
;
2)
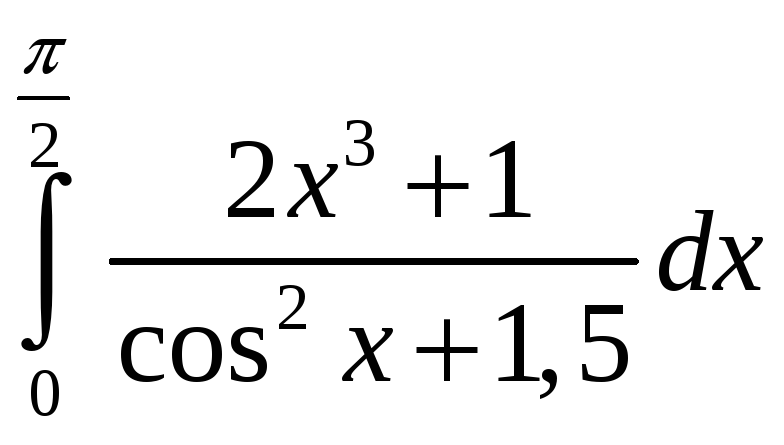 .
.
3.2.11
1)
![]() ;
2)
;
2)
![]() .
.
3.2.12
1)
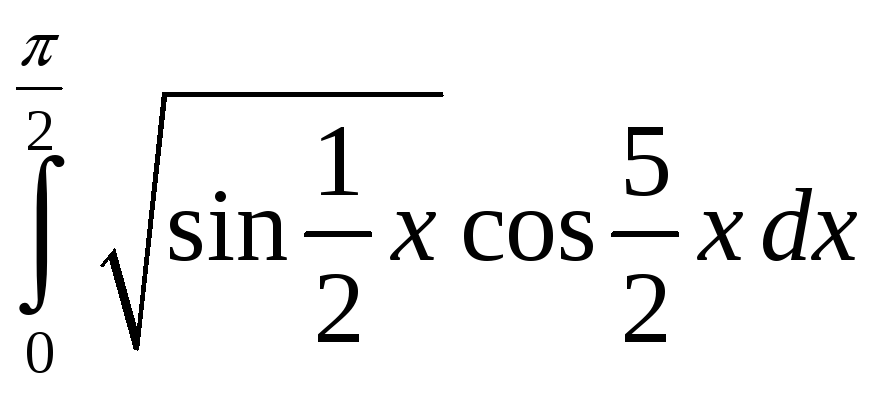 ;
2)
;
2)
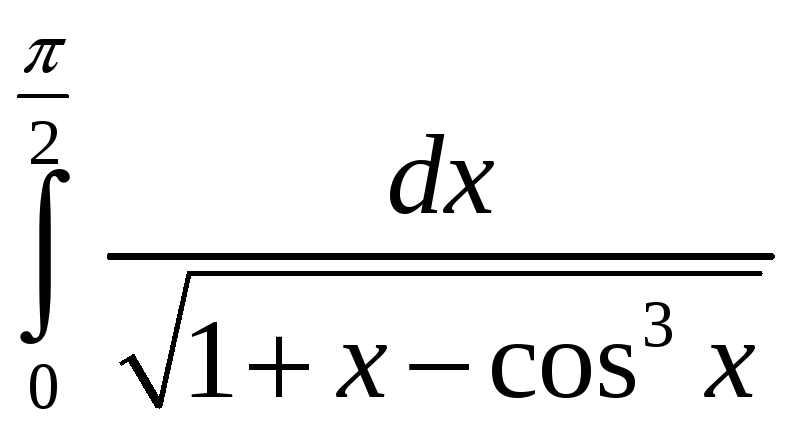 .
.
3.2.13
1)
![]() ;
2)
;
2)
![]() .
.
3.2.14
1)
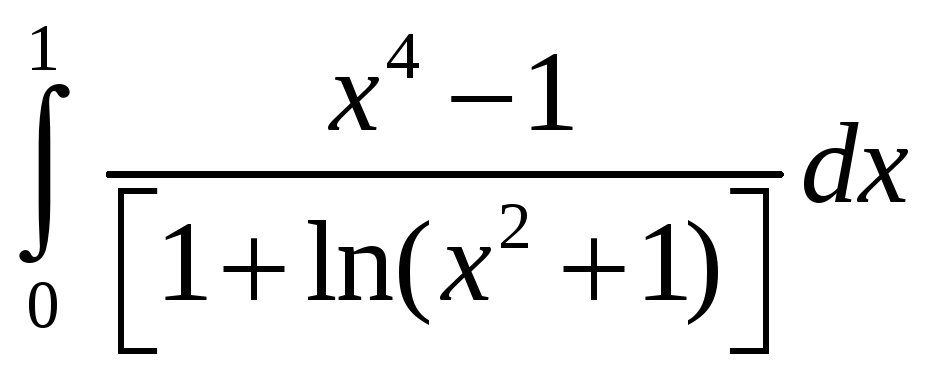 ;
2)
;
2)
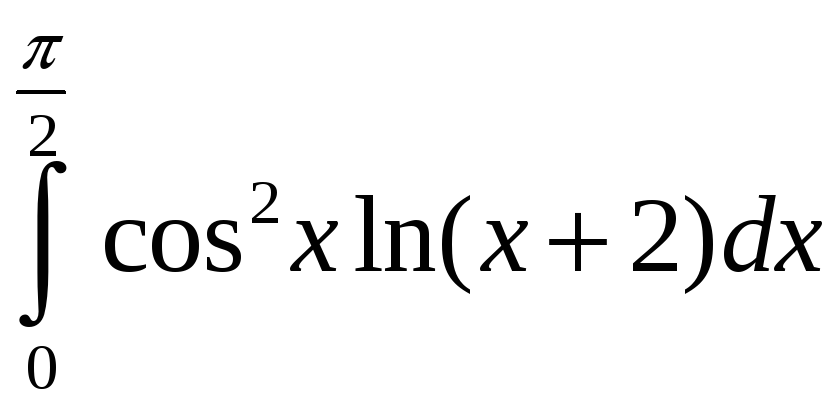 .
.
3.2.15
1)
![]() ;
2)
;
2)
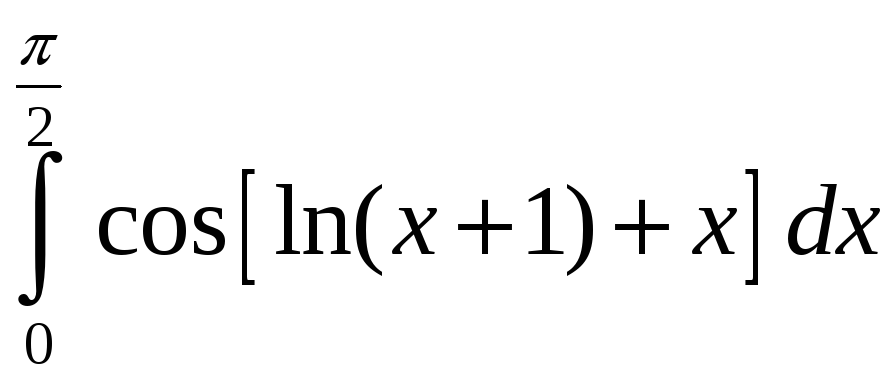 .
.
3.2.16
1)
![]() ;
2)
;
2)
![]() .
.
3.2.17
1)
![]() ;
2)
;
2)
![]() .
.
3.2.18
1)
![]() ;
2)
;
2)
![]() .
.
3.2.19
1)
![]() ;
2)
;
2)
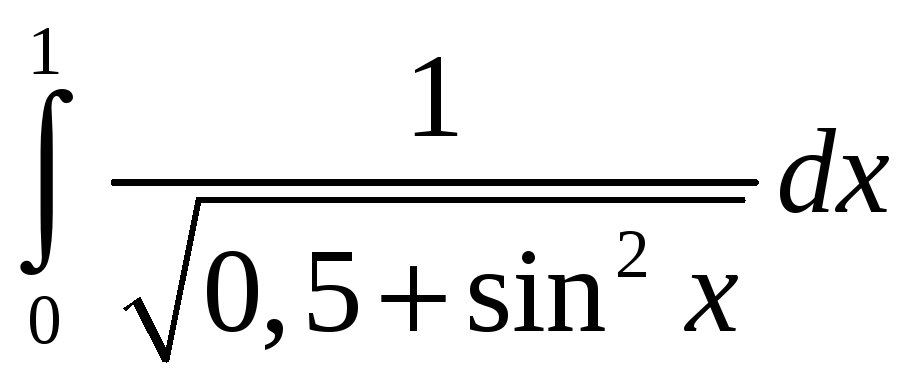 .
.
3.2.20
1)
![]() 2)
2)
![]() .
.
3.2.21
1)
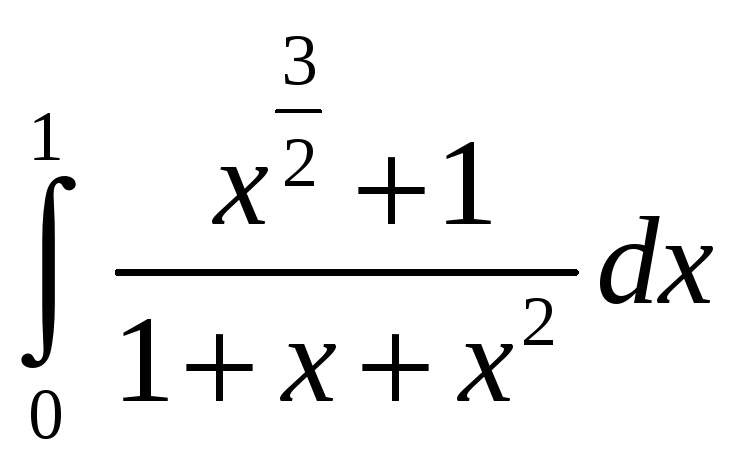 ;
2)
;
2)
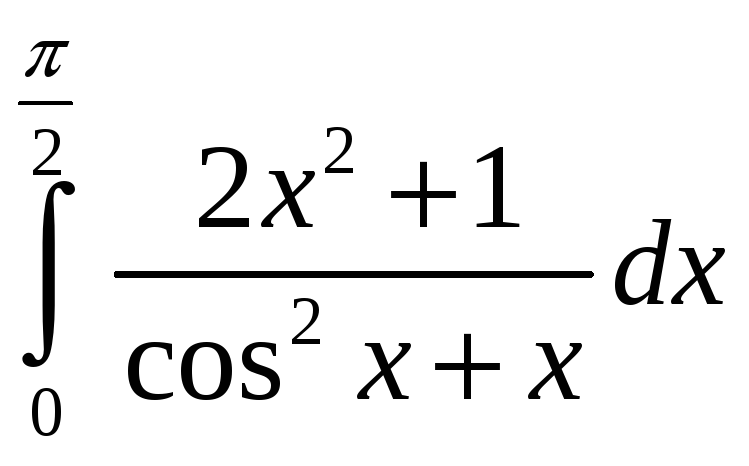 .
.
3.2.22
1)
![]() ;
2)
;
2)
![]() .
.
3.2.23
1)
![]() ;
2)
;
2)
![]() .
.
3.2.24
1)
![]() ;
2)
;
2)
![]() .
.
3.2.25
1)
![]() ;
2)
;
2)
![]() .
.
3.2.26
1)
![]() ;
2)
;
2)
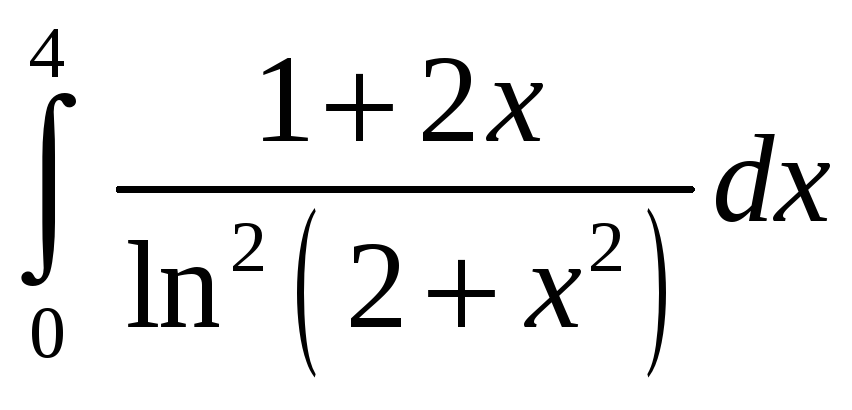 .
.
3.2.27
1)
![]() ;
2)
;
2)
![]() .
.
3.2.28
1)
![]() ;
2)
;
2)
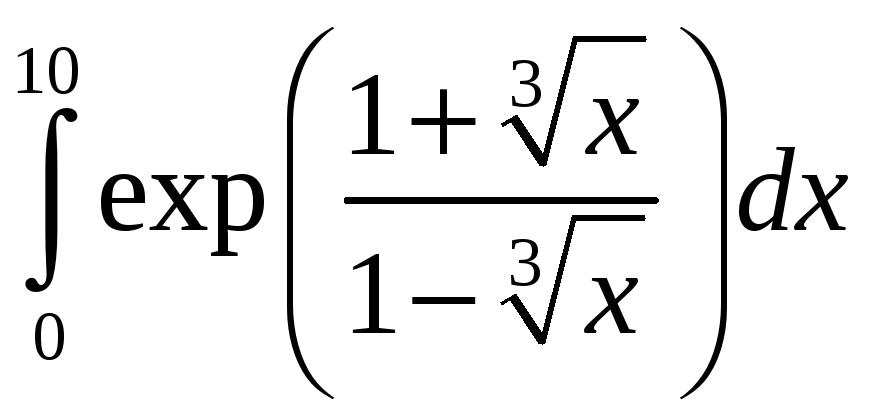 .
.
3.2.29
1)
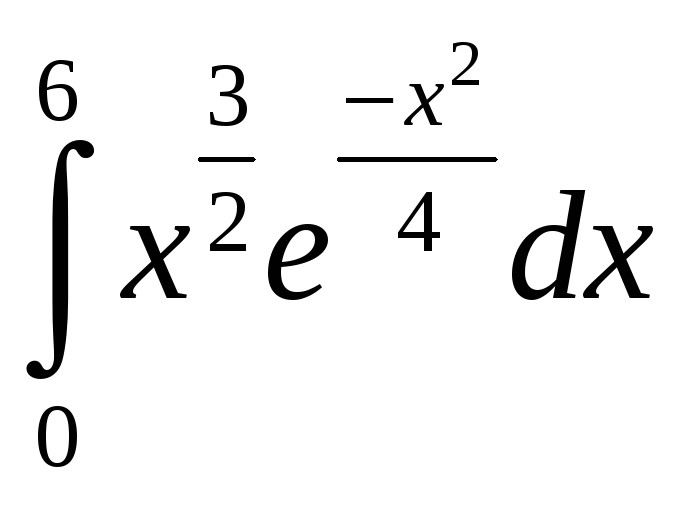 ;
2)
;
2)
![]() .
.
3.2.30
1)
![]() ;
2)
;
2)
![]() .
.
3.3 Приклади виконання лабораторної роботи
Приклад
3.3.1 Обчислити
інтеграл
![]() за формулою прямокутників з точністю
ε=0,01.
за формулою прямокутників з точністю
ε=0,01.
Вирішимо
задачу, використовуючи середовище
Excel.
Треба обчислити функцію![]() на проміжку [0,7;1,3].
на проміжку [0,7;1,3].
Кількість відрізків розбивки проміжку інтегрування визначимо з умови (3.2) :
![]() ,
,
 ,
,
М=2, тоді ![]() ;
;
![]() .
.
Розмістимо початкові значення та таблицю значень x, у у такому вигляді, як показано на рис. 3.1 .
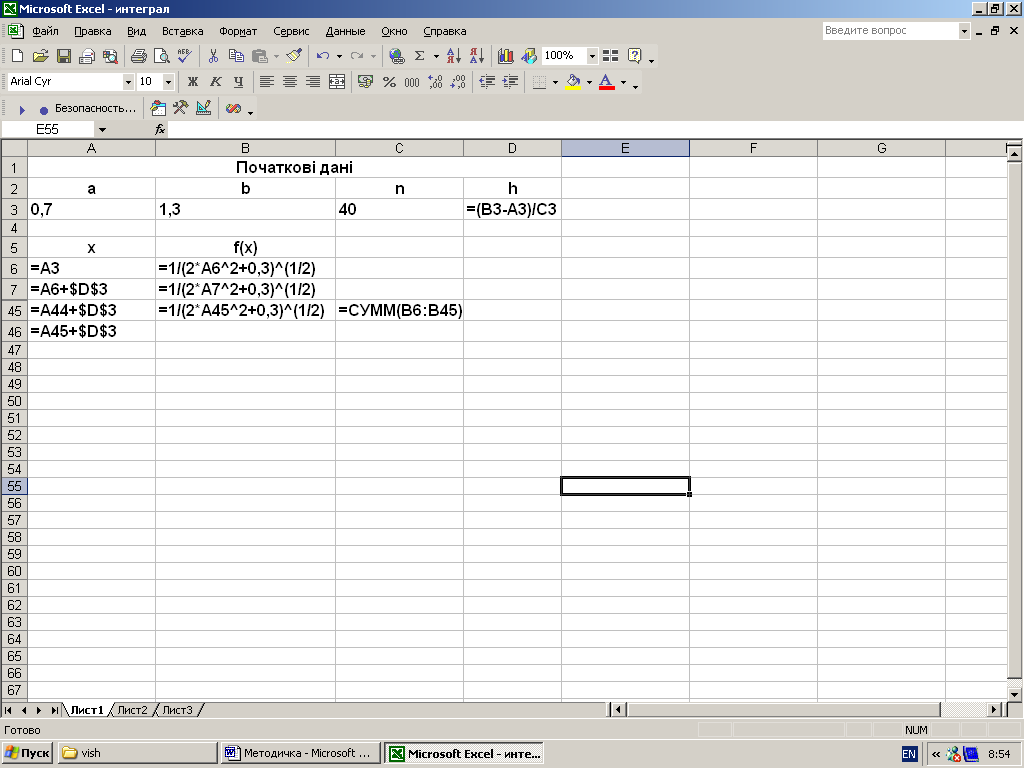


Рисунок 3.1 – Таблиця початкових значень та значень х, у
Згідно
протоколу рішення, який показано на
рис. 3.2 , отримаємо відповідь:
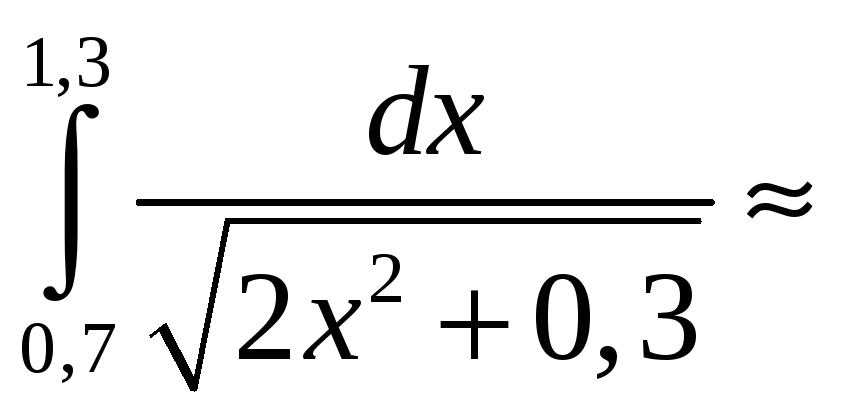 0,406865
.
0,406865
.

Рисунок 3.2 – Протокол рішення інтегралу за формулою прямокутників
Приклад
3.3.2 Обчислити
інтеграл
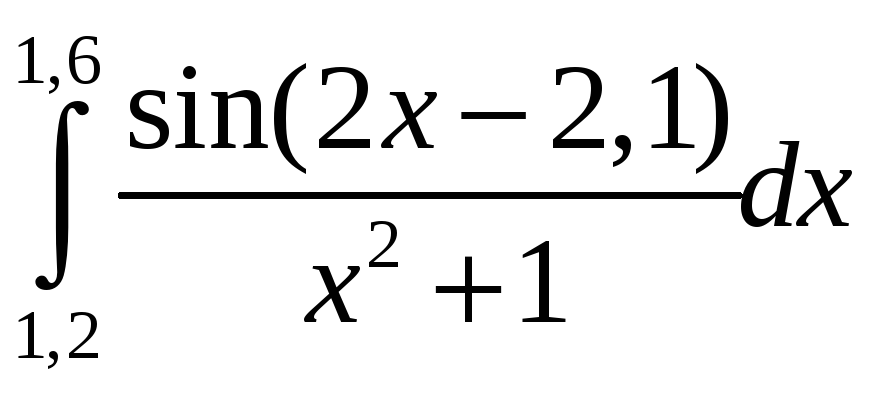 за формулою
за формулою
парабол, уточнювання провести згідно формули Річардсона.
Для
вирішення задачі з’ясуємо початкові
дані: a
= 1,2 ; b
= 1,6
,
![]() ,
оберемо n1
= 10 , n2
= 15
, які розмістимо на листі Excel
з ім’ям „Сімпсона”
. На цьому ж листі розмістимо кнопку
Command
Button1
, як показано на рис. 3.3 та створимо
процедуру рішення.
,
оберемо n1
= 10 , n2
= 15
, які розмістимо на листі Excel
з ім’ям „Сімпсона”
. На цьому ж листі розмістимо кнопку
Command
Button1
, як показано на рис. 3.3 та створимо
процедуру рішення.
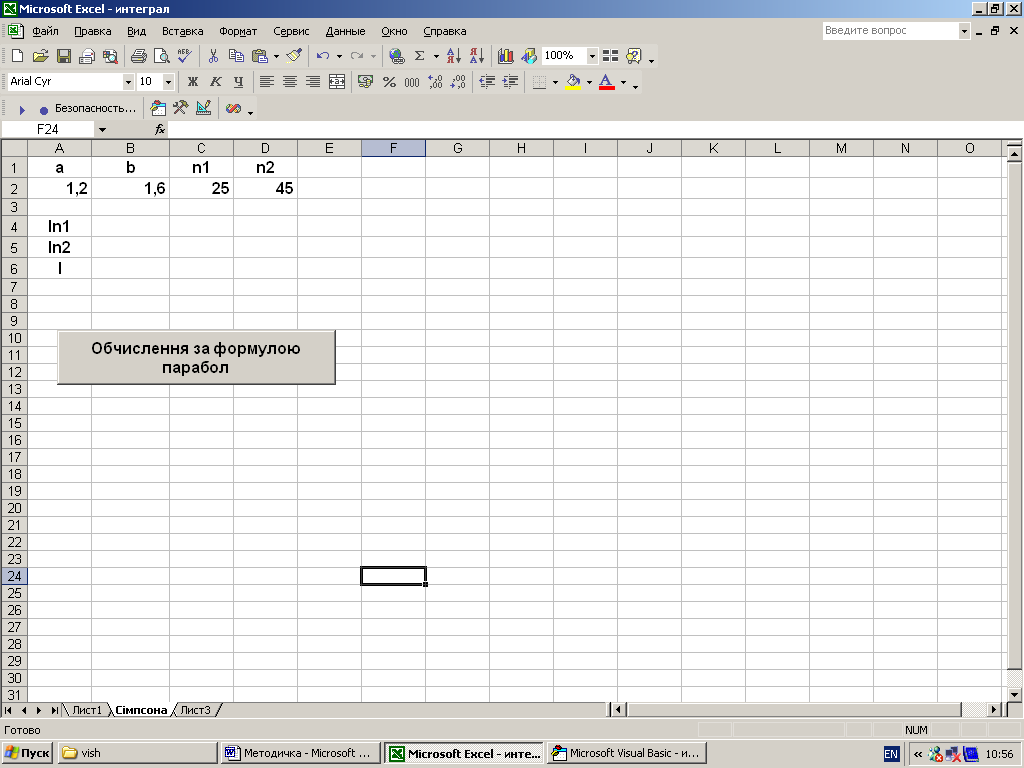
Рисунок 3.3 – Зразок листа Excel з ім’ям „Сімпсона”
Текст процедури:
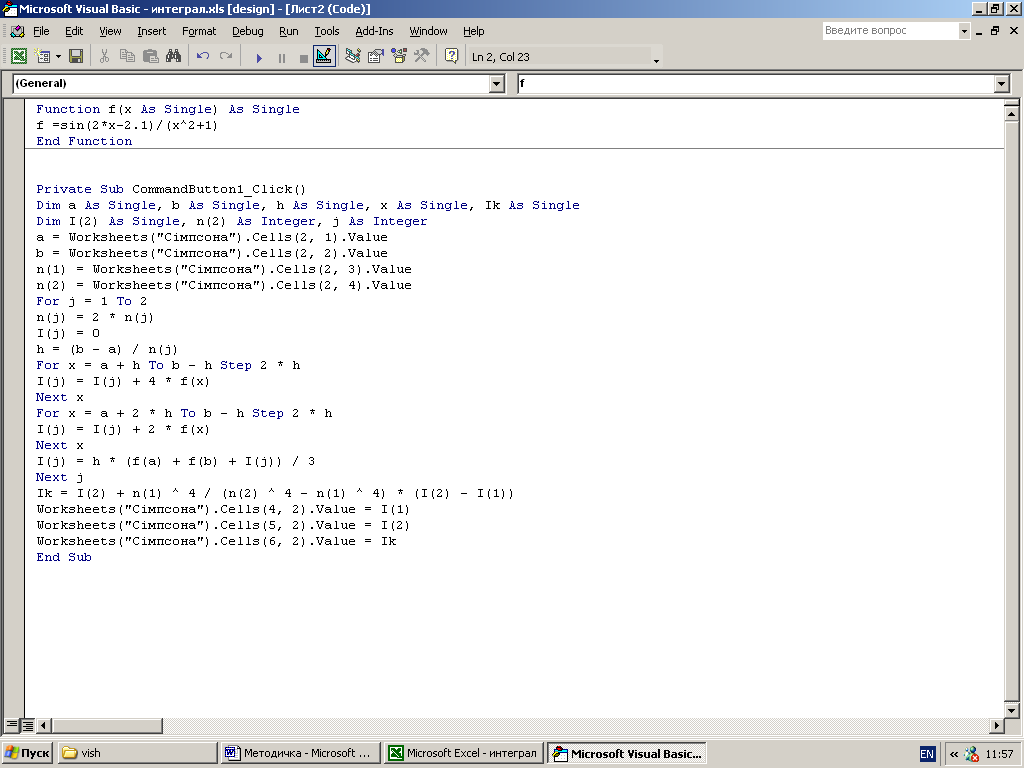
Зразок протоколу рішення наведено на рис. 3.4 .
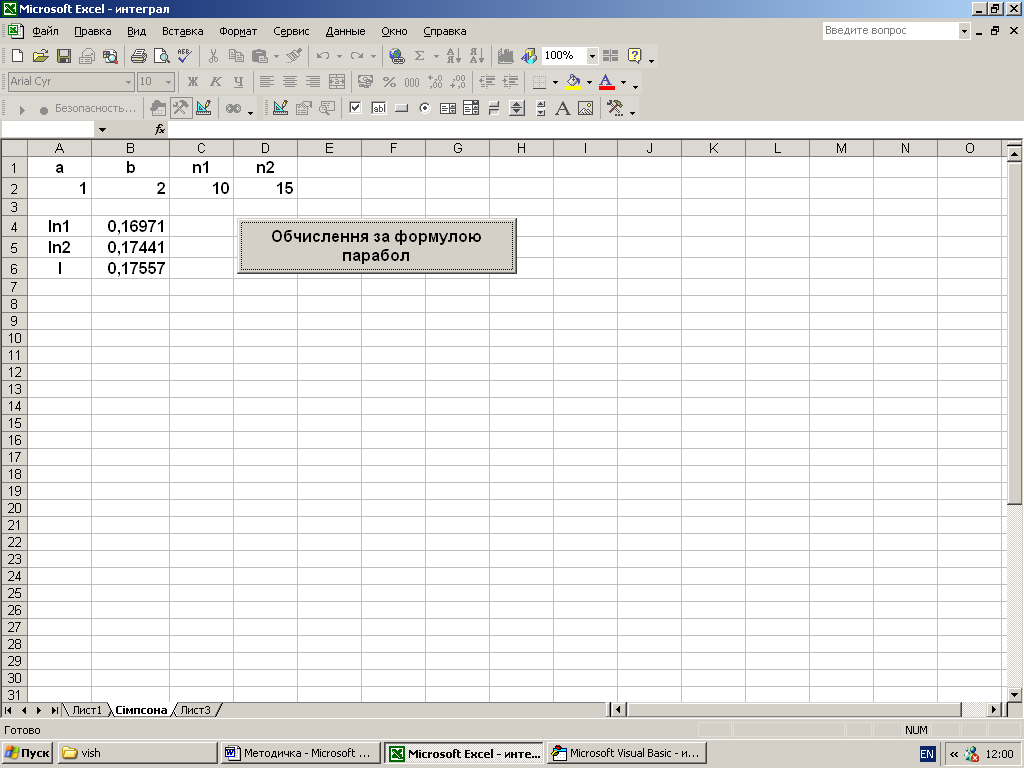
Рисунок 3.4 – Протокол рішення інтегралу за формулою парабол
Згідно протоколу рішення маємо:
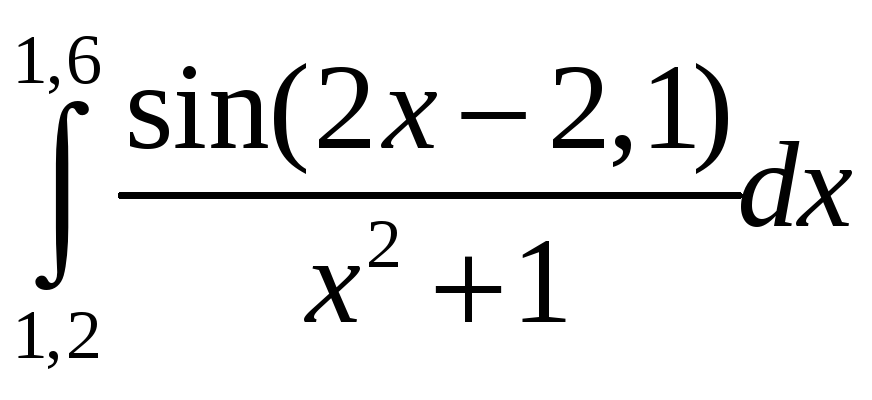 =
0б08389 .
=
0б08389 .
4 Лабораторна робота №4 тема: Наближення (інтерполяція) функцій
4.1 Теоретичні відомості
Задача наближення функції виникає, коли для функції, даної при дискретних значеннях аргументу у вигляді таблиці (ці значення називаються вузлами інтерполяції) необхідно знайти значення функції в проміжних крапках. Накладаючи вимогу, щоб наближена функція у вузлах співпадала з табличними значеннями (рис. 4.1), одержуємо задачу інтерполяції.
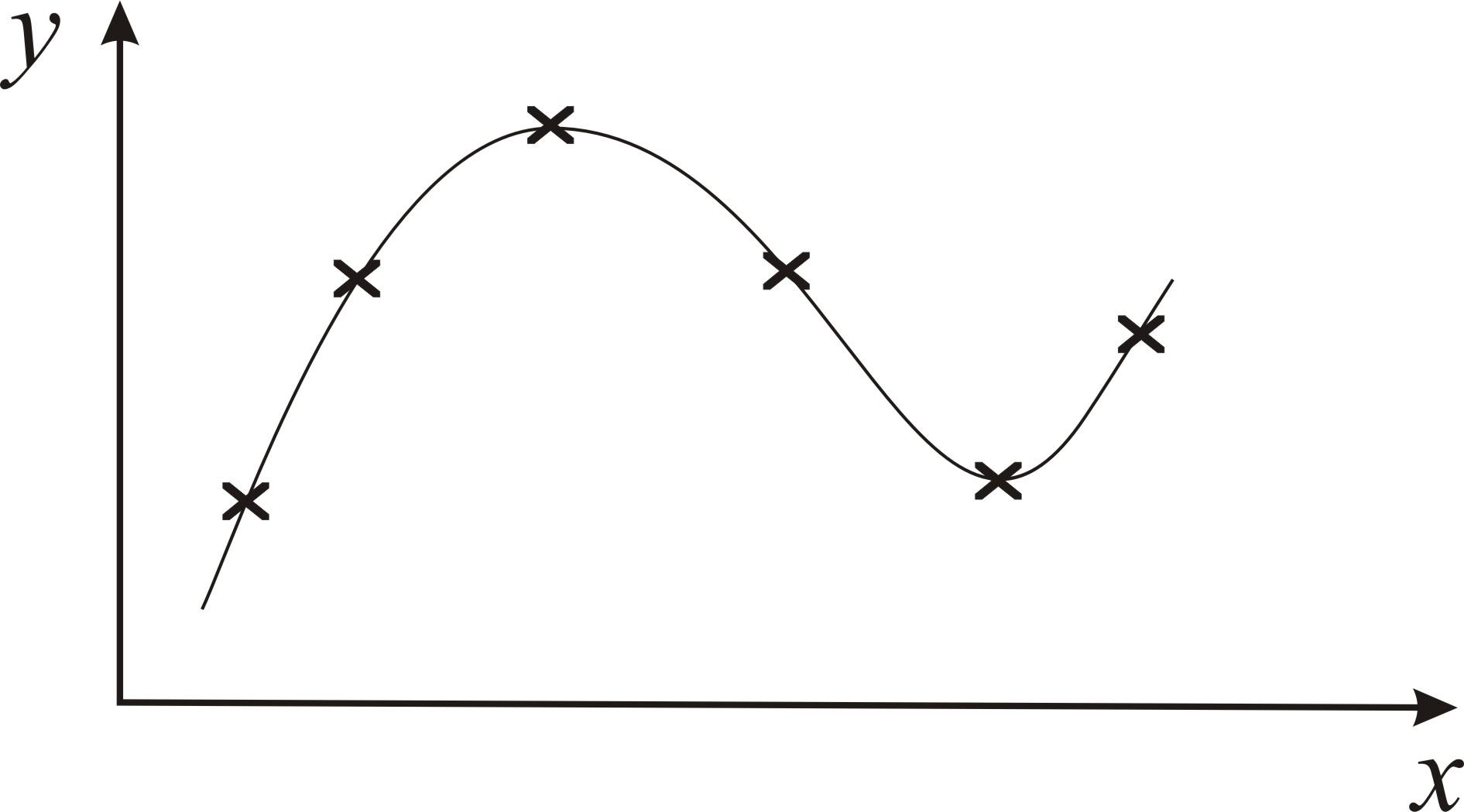
Рисунок 4.1 – Графік наближеної функції
Нехай в результаті спостережень за ходом деякого процесу побудована таблиця:
|
x |
x0 |
x1 |
x2 |
… |
xn |
|
f(x) |
f(x0) |
f(x1) |
f(x2) |
… |
f(xn) |
Тобто, функція f(x) задана таблицею значень для кінцевої множини значень х .
Якщо необхідно знайти значення f(x) для проміжного значення аргументу, то будують функцію φ(x) , просту для обчислень і таку, що для заданих x0 , x1 , x2 , ... , xn приймає значення f(x0) , f(x1) , f(x2) , ... , f(xn) .
В інших точках відрізка [x0, xn] вважаємо, що φ(x) приблизно визначає функцію f(x) з тим чи іншим ступенем точності.
Найчастіше, функцію φ(x) представляють у вигляді алгебраїчного багаточлена деякого ступеня.
Найпростіша інтерполяція – це лінійна, тобто, коли невідому аналітичну залежність f(x) замінюють відрізками прямих, які проходять через відповідні вузли інтерполяції. В цьому випадку потрібно визначити якому відрізку належить надане х* і за формулою лінійної інтерполяції знаходять f(x*) . Якщо xi <= x* <= xi+1 , то відповідна пряма проходить через вузли (xi , f(xі)) , (xi+1 , f(xі+1)) :
![]() (4.1)
(4.1)
Точність підрахунків в цьому випадку незначна, тому що враховується вплив тільки 2-ох вузлів інтерполяції. Частіше будують багаточлен Pn(x) ступеня n , що в (n+1) даних точках x0 , x1 , x2 , ... , xn . приймає дані значення y0 = f(x0) , y1 = f(x1) , … , yn = f(xn) , тобто
f(xі) = Pn(xі) , (і = 0, 1, 2, ... , n) .
Відзначимо, що двох різних інтерполяційних багаточленів одного і того же ступеня n існувати не може. Цим умовам задовольняє інтерполяційний багаточлен Лагранжа:
![]() (4.2)
(4.2)
Тоді 
