
- •Введение
- •Выражение для передаточной функции разомкнутой системы
- •2. Выражение и построение афх w(j) разомкнутой системы с использованием пакета моделирования Matlab
- •3.Оценка устойчивости замкнутой системы с помощью критерия Гурвица:
- •4.Оценка устойчивости замкнутой системы с помощью критериев Михайлова
- •5.Оценка запасов устойчивости системы по модулю и по фазе, пользуясь афх
- •Построение лах и лфх разомкнутой системы в Matlab. Оценка запасов устойчивости системы по модулю и по фазе.
- •График переходной функции заданной нескорректированной системы. Оценка показателей качества нескорректированной системы
- •8. Синтез последовательного корректирующего устройства методом Соколова.
- •9. Построение лах и лфх скорректированной разомкнутой системы в Matlab
- •Заключение
- •Список литературы

задание
к курсовой работе по «ТАУ»
«Комплексный анализ следящей системы»
Объектом исследования является следящая система, структурная схема которой представлена на рис. 1.
 Рис. 1. Структурная
схема следящей системы.
Рис. 1. Структурная
схема следящей системы.
Кизм - передаточный коэффициент измерительного устройства;
Кфчв, Тф - коэффициент передачи и постоянная времени фазочувствительного выпрямителя;
Ку - коэффициент усиления электронного усилителя;
Кэму, Тэму - коэффициент передачи и постоянная времени электромашинного усилителя;
Кд, Тд - коэффициент передачи и постоянная времени электрического двигателя;
Кред - коэффициент передачи редуктора.
Исходные данные для моделирования приведены ниже:
Таблица 1
|
№ вар. |
Кизм, В / град |
Ку, В / град |
Кэму, В / мА |
Тэму, сек |
Кд |
Тд, сек |
Кред |
Кфчв
|
Тф, сек |
Требуемые показатели качества | |
|
|
tр | ||||||||||
|
4 |
30 |
1 |
3,8 |
0,028 |
4 |
0,2 |
0,002 |
0,9 |
0,005 |
20 |
2,0 |
Содержание
Введение 5
1.Выражение для передаточной функции разомкнутой системы 6
2. Выражение и построение АФХ W(j) разомкнутой системы с использованием пакета моделирования Matlab 7
4.Оценка устойчивости замкнутой системы с помощью критериев Михайлова 9
6.Построение ЛАХ и ЛФХ разомкнутой системы в Matlab. Оценка запасов устойчивости системы по модулю и по фазе. 11
7.График переходной функции заданной нескорректированной системы. Оценка показателей качества нескорректированной системы 14
8. Синтез последовательного корректирующего устройства методом Соколова. 15
Заключение 19
Список литературы 20
Введение
Существует чрезвычайно большое разнообразие автоматических систем, выполняющих те или иные функции по управлению самыми разными физическими процессами во всех областях техники. В этих системах сочетаются весьма разнообразные по конструкции механические, электрические и другие устройства, составляя, в общем, сложный комплекс взаимодействующих друг с другом звеньев.
В теории автоматического управления основными являются следующие проблемы: устойчивости, качества переходных процессов, статической и динамической точности, автоколебаний, оптимизации, синтеза. Задачи общей теории автоматического управления заключаются в решении перечисленных проблем.
Темой курсовой работы является комплексный анализ следящей системы.
Следящая система – это система, на выходе которой с определенной точностью воспроизводится произвольное во времени изменение какой-нибудь величины, поданной на вход.
Целью курсовой работы является проектирование и исследование систем автоматического управления техническими объектами. В соответствии с заданием необходимо провести исследование динамических характеристик и синтез корректирующего устройства следящей системы для обеспечения показателей качества управления: заданных величин перерегулирования и времени регулирования.
В схеме используется принцип управления по отклонению (принцип обратной связи).
Выражение для передаточной функции разомкнутой системы
Передаточная функция является важной категорией в теории автоматического управления, так как является математической моделью системы и полностью характеризует её динамические свойства.

2. Выражение и построение афх w(j) разомкнутой системы с использованием пакета моделирования Matlab
а)
Амплитудно-фазовая
характеристика (АФХ)
– это график
частотной передаточной функции
![]() ,
построенная на комплексной плоскости:
,
построенная на комплексной плоскости:
![]()
АФХ разомкнутой системы:
Сделаем замену
![]() в
передаточной функции
в
передаточной функции
![]() и
получим
и
получим
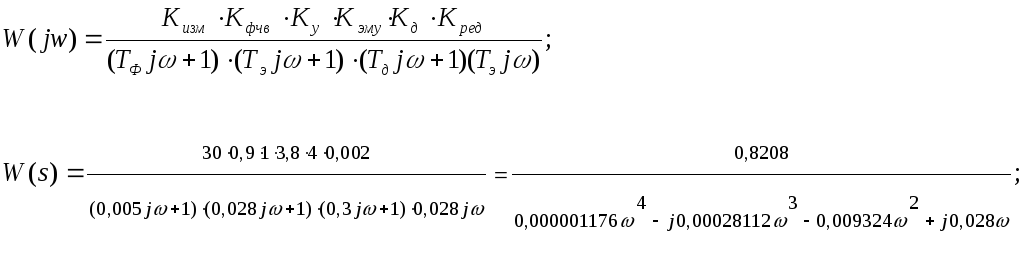
Листинг программы:
>> num=[0.8208];
>> den=[0.000001176 0.00028112 0.009324 0.028 0];
>> w=12:0.1:100;
>> AFH=freqs(num,den,w);
>> u=real(AFH);
>> v=imag(AFH);
>> plot(u,v);
>> grid;

Рис. 2 – График АФХ
![]() разомкнутой системы
разомкнутой системы
3.Оценка устойчивости замкнутой системы с помощью критерия Гурвица:
Характеристический
полином замкнутой системы
![]() представляет
собой полином знаменателя передаточной
функции замкнутой системы, который
равен сумме полиномов числителя и
знаменателя передаточной функции
разомкнутой системы.
представляет
собой полином знаменателя передаточной
функции замкнутой системы, который
равен сумме полиномов числителя и
знаменателя передаточной функции
разомкнутой системы.
Характеристический полином замкнутой системы:
![]()
![]() (1)
(1)

Алгебраический критерий устойчивости Гурвица:
Если характеристическое уравнение системы имеет вид (1), то для устойчивости системы необходимо и достаточно, чтобы при а0>0 главный определитель Гурвица n и все его диагональные миноры (1, 2, …n-1) были положительными.


Так как определитель Гурвица и все его диагональные миноры больше нуля, система устойчива.
Также на основании критерия Гурвица можно получить, что для уравнения четвертого порядка с положительными коэффициентами требуется выполнение условия:
![]() тогда
тогда
![]() значит, система устойчива.
значит, система устойчива.
