2.6. Анализ линейных дискретных систем во временной области

Суть задачи анализа.Пусть имеется некоторая дискретная система, представленная разностными уравнениями в форме Коши, либо уравнениями "вход-выход". В частности, эти уравнения могут представлять замкнутую систему автоматического управления (импульсную или цифровую), для непрерывной части которой построена соответствующая дискретная модель.

Суть всякой задачи анализа во временной области, в том числе и для дискретных систем, состоит в том, чтобы при заданном внешнем воздействии на систему и при заданных начальных состояниях (начальных условиях) найти реакцию выхода этой системы, а также других ее переменных, которые могут представлять какой-либо интерес и определять поведение данной системы. Очевидно, что математически эта задача сводится к решению разностных уравнений, описывающих данную систему.

Решение разностных уравнений, представленных в форме Коши.Рассмотрим линейную дискретную систему, представленную с помощью разностных уравнений состояний с постоянными коэффициентами

(2.6.1)

где ,,- векторы дискретных состояний, входов и выходов соответственно;,,- числовые матрицы соответствующих размеров.

Решить разностное уравнение (2.6.1) это значит, при заданной решетчатой функции входного воздействия и при заданном начальном состоянии, найти решетчатые векторные функции состоянияи выходадля. Очевидно, что решение данной задачи может быть получено с помощью итерационной процедуры, вытекающей непосредственно из уравнения дискретных состояний (2.6.1). Действительно, запишем это уравнение для моментов.

Продолжая эти итерации легко увидеть, что для произвольного момента будем иметь

. (2.6.2)

Полученное выражение позволяет аналитически определить решение разностного уравнения (2.6.1) и представляет собой аналог формулы Коши для непрерывных систем. При этом следует заметить, что для ненулевого начального момента совершенно аналогично можно получить для

. (2.6.3)

В формулах (2.6.2) и (2.6.3) матричная функция есть не что иное, как нормированная фундаментальная матрица стационарной дискретной системы (2.6.1).

Рассмотрим один из способов аналитического определения матрицы . При этом ограничимся случаем, когда все собственные числаматрицыразличны. Напомним, что они могут быть определены как корни характеристического уравнения

. (2.6.4)

Пусть также - обозначают собственные векторы матрицы. Образуем из этих векторов матрицу, которая по построению является неособой. Тогда, как известно из теории матриц[11], можно записать

,.

В результате для матричной функции будем иметь

.

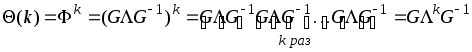При этом очевидно, что , и таким образом окончательно получим

. (2.6.5)

Существуют и другие способы нахождения этой матричной функции.

Заметим, что в более общем нестационарном случае, когда элементами матриц системы (2.6.1) являются решетчатые функции, формула (2.6.3) принимает вид [6]

,,

где нормированная фундаментальная матрица становится функцией двух дискретных аргументов и определяется как решение следующего матричного разностного уравнения

, , . (2.6.6)

Возвращаясь к стационарному случаю нетрудно заметить, что матричная функция также удовлетворяет уравнению (2.6.6).

Решение разностных уравнений в форме "вход-выход".При рассмотрении этого вопроса ограничимся случаем односвязной (один вход, один выход) системы с постоянными параметрами. Разностное уравнение этой системы, представленное в форме "вход-выход" имеет вид

,, (2.6.7)

где ,- известные числа, причем.

Пусть входное воздействие представляет собой известную решетчатую функцию, заданную для, и пусть заданы начальные условия, определяемыескалярными соотношениями

. (2.6.8)

Требуется определить решетчатую функцию выхода для.

Переходя к решению этой задачи, отметим, что если задано, то вся правая часть уравнения (2.6.7) становится известной решетчатой функцией, которую обозначим как. Таким образом задача сводится к нахождению решения неоднородного линейного разностного уравнения с известной правой частью

. (2.6.9)

Наряду с уравнением (2.6.9) рассмотрим соответствующее ему однородное уравнение

. (2.6.10)

Обозначим через некоторое нетривиальное решение этого уравнения, которое будем искать в виде, гденекоторое число. Подставляя функциюв уравнение (2.6.10) получим

.

Отсюда следует, что должно быть ненулевым корнем следующего уравнения

, (2.6.11)

которое, очевидно, является характеристическим, и которое при имеетненулевых корней. Пусть для простоты все корни различны. Тогда для однородного уравнения (2.6.10) можно построитьчастных решений, которые образуют линейно-независимую систему решетчатых функций[4]. Это означает, что линейная комбинация этих решений

, (2.6.12)

где - некоторые константы, также будет решением уравнения (2.6.10). Действительно, если обозначить характеристический полином каки учесть, что, то, подставляя (2.6.12) в уравнение (2.6.10), получим

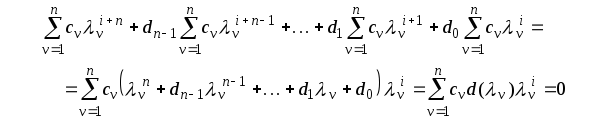
Очевидно, что любое другое решение уравнения (2.6.10) можно представить в виде (2.6.12), и таким образом (2.6.12) определяет собой общее решение однородного уравнения.

Если среди корней характеристического полинома есть комплексный корень , то поскольку коэффициенты этого полинома вещественны, найдется и сопряженный к нему корень, причемибудут входить в линейную комбинацию (2.6.12) с комплексно-сопряженными коэффициентамии. Сумма двух комплексно-сопряженных членовможет быть записана как

Таким образом, в случае отсутствия кратных корней, общее решение разностного уравнения (2.6.10) представляется линейной комбинацией решетчатых функций,,, где- вещественные корни, аи- модули и аргументы комплексно-сопряженных корней.

Если среди корней имеются кратные, то можно показать [4], что функции(, - число некратных корней) будут образовывать систему линейно-независимых решений, если каждому кратному корнюкратностипоставить в соответствие частное решение вида

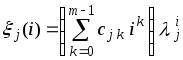, (2.6.13)

где - некоторые постоянные.

Рассмотрим теперь решение неоднородного уравнения (2.6.9). Для этого предположим, что частное решение этого уравнения , обусловленное правой частью, определено. Его обычно называют вынужденным решением, и оно может быть найдено, например, по виду правой части (2.6.9), аналогично тому, как это делается для непрерывных систем при нахождении решения линейного неоднородного дифференциального уравнения с известной правой частью[12]. Другим способом нахождения вынужденного решенияявляется метод вариации произвольных постоянных[4].

Покажем теперь, что искомое общее решение неоднородного уравнения (2.6.9) определяется выражением

, (2.6.14)

где - общее решение однородного уравнения (2.6.10). Для этого подставим (2.6.14) в исходное уравнение (2.6.9). Получим

. (2.6.15)

Функция является частным решением неоднородного уравнения, поэтому

,

а функция есть общее решение однородного уравнения, и, следовательно, первое слагаемое из (2.6.15), заключенное в скобки, равно нулю. Таким образом подстановка (2.6.14) в исходное уравнение обращает его в тождество, и таким образом (2.6.14) действительно есть общее решение неоднородного уравнения. В частном случае, если все корни характеристического полинома различны, то с учетом (2.6.12) это решение примет вид

, (2.6.16)

где постоянные могут быть определены по заданным начальным условиям (2.6.8).

Весовая и переходная функции (матрицы) дискретной системы.Пусть дискретная система задана разностными уравнениями в форме Коши (2.6.1). Используя решение (2.6.2) запишем выражение для выходной переменной

,. (2.6.17)

В этом выражении матричная функция

(2.6.18)

называется импульсной переходной или весовой матрицей дискретной системы, а матричная функция

(2.6.19)

называется переходной матрицей этой системы.

Чтобы выяснить физический смысл этих характеристик рассмотрим систему с одним входом и одним выходом . В этом случае характеристики (2.6.18) и (2.6.19) становятся скалярными, которые будем обозначать какисоответственно.

Пусть в начальный момент система (2.6.1) находилась в покое, то есть, и пусть в моментна систему действует единичный импульс, определяемый соотношением

. (2.6.20)

Тогда очевидно, что вплоть до момента выход системы будет нулевым, а прииз (2.6.17) получим

.

Таким образом, весовая функция дискретной системы это реакция ее выхода при нулевом начальном состоянии на единичный импульс (2.6.20).

Определим теперь при выход дискретной системы, когда на ее входе в моментдействует единичная ступенчатая решетчатая функция, определяемая соотношением

. (2.6.21)

Тогда из (2.6.17) для будем иметь

,

то есть переходная функция это реакция выхода системы при нулевом начальном состоянии на единичную ступенчатую функцию.

Очевидно, что в многомерном случае элементами весовой матрицыявляются решетчатые функции, определяющие реакцию соответствующего выхода дискретной системы при нулевом начальном состоянии, когда на один из входов действует единичный импульс, а на остальных входах сигналы отсутствуют. Аналогично определяются элементы переходной матрицы.

Рассмотрим особенность нахождения переходной функции для дискретной односвязной (для простоты) системы заданной в форме "вход-выход" разностным уравнением (2.6.7). Эта особенность состоит в том, что начальные условия по выходной переменной (2.6.8) определяются не только начальным состоянием системы, которое при нахождении переходной функции принимается нулевым, но зависят также и от решетчатой функции входного воздействия. Это приводит к тому, что начальные условия (2.6.8) могут оказаться ненулевыми. Формально это можно объяснить также тем, что из-за наличия в правой части уравнения (2.6.7) смещенных решетчатых функций ступенчатое воздействие (2.6.21) начинает действовать на систему уже в момент.

Определить начальные условия (2.6.8) можно непосредственно из самого уравнения (2.6.7). Для этого, полагая и принимая очевидное условие, чтодля, запишем это уравнение для моментов. Тогда нетрудно показать, что начальные условия определятся следующими соотношениями

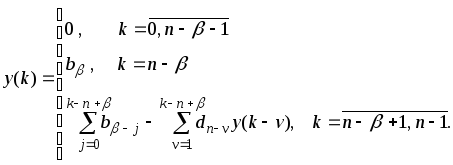(2.6.22)

Заметим, что если до момента система находилась в покое, то начальные условия (2.6.8) могут оказаться ненулевыми не только при. В частности, если в более общем случае

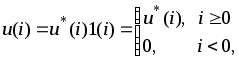
где - заданная решетчатая функция, то начальные условия также могут быть определены по соотношениям (2.6.22), в которых коэффициентынеобходимо теперь умножить на, где.

Пример.В качестве примера рассмотрим односвязную дискретную систему 3-го порядка, заданную в форме "вход-выход" следующим разностным уравнением

. (2.6.23)

Пусть до момента система находилась в покое и пусть входное воздействиезадано следующей решетчатой функцией

. (2.6.24)

Требуется определить решетчатую функцию выхода .

Переходя к решению данной задачи, составим характеристическое уравнение

,

решением которого являются следующие корни

,.

Тогда общее решение соответствующего однородного уравнения запишется в виде

,

где ,,- произвольные постоянные.

Найдем вынужденную составляющую решения. При этом, поскольку в силу (2.6.24) правая часть заданного разностного уравнения является гармонической решетчатой функцией, то и вынужденное решение также будем искать в виде гармонической решетчатой функции той же частоты

, (2.6.25)

где инеизвестные пока константы. Для их определения подставим (2.6.25) и (2.6.24) в исходное уравнение

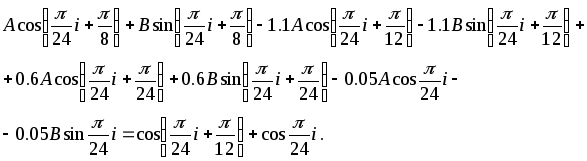
Применяя формулы для и, после преобразования и приведения подобных, получим следующую систему уравнений

решениями которой будут и. Таким образом окончательно общее решение заданного неоднородного уравнения (2.6.23) запишется в виде

(2.6.26)

Определим постоянные . Для этого найдем сначала начальные условия,,. Записывая исходное уравнение (2.6.23) для моментови учитывая, чтопри, а также условие (2.6.24) будем иметь

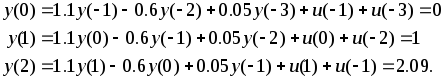
Запишем теперь решение (2.6.26) для моментов . Производя необходимые вычисления, получим следующую систему уравнений

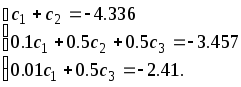
Решениями этой системы являются

,,.

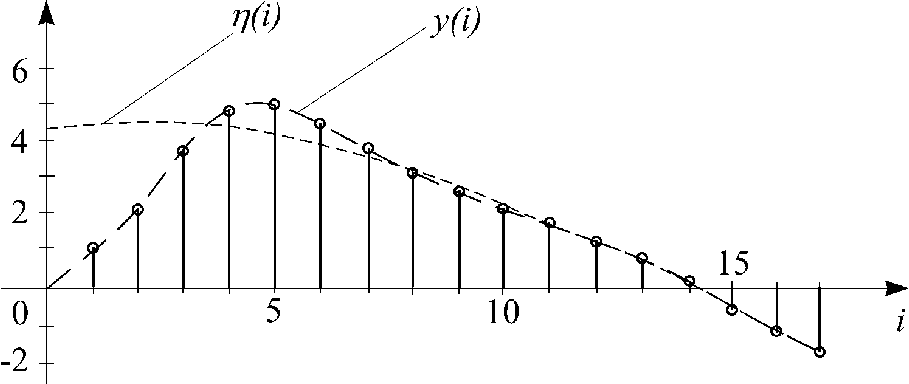
Рис. 2.7.

Таким образом окончательно искомое решение определится следующей решетчатой функцией

.

На рис.2.7приведены графики решетчатых функций найденного решенияи вынужденной составляющей этого решения. Заметим, что как следует из (2.6.26) и из приведенного рисунка, если свободная составляющаяпри, то установившаяся реакция дискретной системы на гармоническое входное воздействие также является гармонической решетчатой функцией той же частоты, но другой амплитуды и фазы.

49