Глава 2.Математические модели и анализ дискретных систем во временной области

2.1. Решетчатые функции и разностные уравнения

Элементарные понятия теории решетчатых функций.Наряду с непрерывными функциями, определёнными на всей вещественной прямой, в теории дискретных систем рассматривают функции, которые определены только в некоторых точках. Такие функции называют решетчатыми. В дальнейшем будем рассматривать только такие решётчатые функции, которые определены в равноотстоящих точках, где–любое целое число, а–период дискретности. Эти функции имеют своим аргументом дискретное время, поэтому их принято обозначать как.

Рис. 2.1.

Любой непрерывной функцииможно поставить в соответствие некоторую решётчатую функцию(рис.2.1, а, б), которая может быть получена из непрерывной функции путём её квантования по времени в моменты, то есть. Очевидно, что обратное утверждение является неверным, так как для одной и той же решётчатой функцииможно поставить в соответствие бесчисленное множество непрерывных функций, совпадающих в моментысо значениями решётчатой функции.

Отметим, что для непрерывной функции можно получить множество решётчатых функций, если рассматривать непрерывную функцию в моменты. При этом для каждого фиксированного значениямы будем иметь решётчатую функцию, которая определена в точках(рис.2.1, в). Такие функции называются смещёнными решётчатыми функциями. Аргументами этих функций являются дискретное времяи параметр. Поэтому их принято обозначать как.

По аналогии с непрерывными функциями, для которых определены понятия производных, для решётчатых функций вводятся понятия конечных разностей. Конечной разностью первого порядка (или для краткости – первой разностью) решётчатой функцииназывается решётчатая функция, определяемая выражением

. (2.1.1)

Аналогично вводятся понятия конечных разностей более высоких порядков. В частности, конечная разность -го порядка (-я разность) определяется как

. (2.1.2)

При этом нулевая разность – это сама решётчатая функция  .

Разность любого порядка можно выразить через значения решётчатой функции . В частности, для второй разности с учётом (2.1.1) получим

.

В общем случае, конечную разность -го порядка можно выразить через значения решётчатой функции для моментов.

Отметим, что вычисление конечных разностей является линейной операцией. Это вытекает непосредственно из определения конечной разности. В частности, например, для первой разности можно записать

,

где –некоторые постоянные.

Аналогом интеграла в теории решётчатых функций выступает понятие суммы. Суммой решётчатой функции называется некоторая решётчатая функция, определяемая выражением

, (2.1.3)

и для которой является первой разностью, то есть

. (2.1.4)

По аналогии с теорией непрерывных функций, решётчатую функцию , определяемую условиями (2.1.3), (2.1.4), называют первообразной для решётчатой функции.

Отметим, что если решётчатая функция определена при всех целочисленных значениях аргумента, то для определения первообразной необходимо дополнительно потребовать, чтобы при каждом конечномсходился ряд. При этом условии первообразная определяется выражением

. (2.1.5)

Нетрудно показать, что если является первообразной для, то для любого постоянногофункциятакже является первообразной для решётчатой функции. Действительно,

.

Таким образом, общий вид первообразной для решётчатой функции определяется формулой

. (2.1.6)

Значение постоянной можно выразить через значениепри некотором фиксированном значении аргумента, то есть

.

Подставляя это выражение в формулу (2.1.6), получим

,

откуда для любого

. (2.1.7)

Эта формула является аналогом формулы Ньютона-Лейбница, связывающей интеграл с первообразной. Основываясь на формуле (2.1.7) можно, в частности, показать [4], что для решётчатых функций справедлива формула суммирования по частям, аналогичная формуле интегрирования по частям для обычных функций.

Разностные уравнения как модели дискретных систем.Всякое соотношение, связывающее решётчатую функцию и её конечные разности, называется разностным уравнением. Подобные уравнения являются аналогом дифференциальных уравнений в теории обычных (непрерывных) функций и также, как и в непрерывных системах, используются для моделирования дискретных динамических процессов. При этом наиболее распространёнными формами представления дискретных систем являются форма Коши и форма "вход-выход". Так, например, если некоторая дискретная система имеет векторный входи векторный выход, то в форме Коши эта система представляется следующими разностными уравнениями

(2.1.8)

где –вектор дискретных состояний этой системы, аи–в общем случае нелинейные векторные функции.

В форме "вход-выход" такая система в общем виде запишется следующим образом

, (2.1.9)

где параметр , определяющий порядок старшей разности выхода, называется порядком разностного уравнения;–в общем случае нелинейная-мерная векторная функция.

Отметим, что поскольку конечные разности любого порядка можно выразить через значения решётчатой функции, то обычно разностные уравнения записывают не относительно конечных разностей, а по отношению к значениям решётчатых функций, сдвинутых на определённое число тактов. Так, например, если ограничиться рассмотрением линейных дискретных систем (в этом случае функции ,иявляются линейными), то разностные уравнения в форме Коши (2.1.8) можно представить в виде

(2.1.10)

а представление этой системы в форме "вход-выход" запишется следующим образом

,. (2.1.11)

В уравнениях (2.1.10) и (2.1.11) ,,,и,обозначают матрицы соответствующих размеров. Причём, если система стационарная, то элементами этих матриц являются числа, а в нестационарном случае – решётчатые функции.

Рис. 2.2.

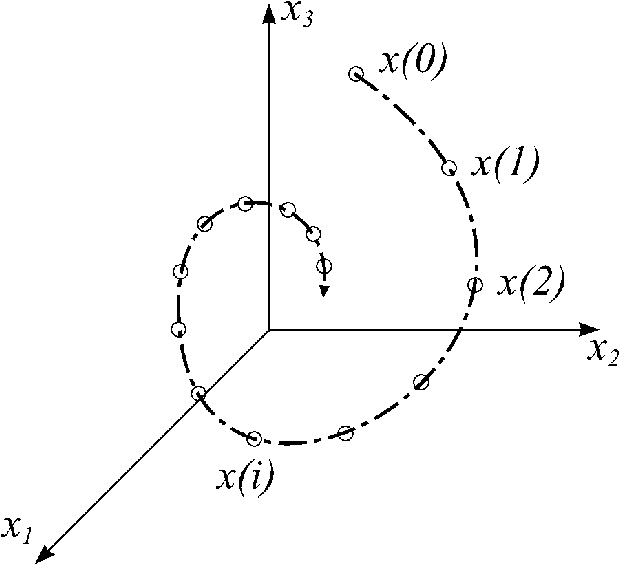
Следует отметить, что число скалярных уравнений в (2.1.9) или число строк матрицив (2.1.11) в общем случае могут и не совпадать с числом выходных переменных. Однако в практических задачах такие системы встречаются весьма редко. Поэтому в дальнейшем будем считать, что число строк в матрицахиравно, и таким образом, матрицыявляются квадратными. Отметим также, что разностные уравнения (2.1.10), представляющие дискретную систему в форме Коши, иногда определяют как уравнение состояний (первое из уравнений (2.1.10)) и уравнение выхода (второе уравнение из (2.1.10)). При этом смысл названия «уравнение состояний» заключается в том, что решение этого уравнения, определённое для некоторого вектора начальных состояний, позволяет получить последовательность дискретных состоянийи представить поведение данной системы в пространстве этих состояний (рис.2.2 – для системы 3-го порядка).

При записи дискретных систем в форме "вход-выход" часто используется операторное представление с применением оператора прямого или обратногосдвига, которые определяются соотношениями

(2.1.12)

где –некоторая решётчатая функция, а–любое положительное целое. Так, например, с применением оператора прямого сдвига уравнение (2.1.11) можно записать в виде

или, если использовать понятие операторных полиномиальных матриц

,,

то (2.1.11) запишется в более компактной форме

. (2.1.13)

Операторное представление (2.1.13) позволяет формально выразить выход дискретной системы через её вход

,

что приводит к понятию операторной передаточной матрицы дискретной системы

. (2.1.14)

Аналогичным образом, при использовании оператора обратного сдвига, уравнение (2.1.11) можно представить в виде

, (2.1.15)

где полиномиальные матрицы иопределяются соотношениями

,.

В справедливости этих формул легко убедиться, если в уравнении (2.1.11) перейти к новому дискретному времени . При этом

,.

Одной из важнейших характеристик разностного уравнения и соответствующей ему дискретной системы является характеристический полином , который, если система представлена в форме Коши (2.1.10), вычисляется по формуле

, (2.1.16)

где –числовые коэффициенты, а–здесь и далее обозначает единичную матрицу соответствующих размеров. Для формы "вход-выход" (2.1.13) характеристический полином определится соотношением

. (2.1.17)

Отсюда в частности следует, что если система имеет скалярный выход , то матричный полиномв уравнении (2.1.13), который теперь становится скалярным, будет совпадать с характеристическим полиномом системы.