2.2. Связь между формами представления дискретных систем

Переход от формы Коши к форме "вход-выход".Рассмотрим дискретную систему, модель которой представлена разностными уравнениями в форме Коши (2.1.10). Найдём представление этой системы в форме "вход-выход" (2.1.11) или (2.1.13). При этом для простоты ограничимся одним частным случаем, когда число переменных состоянияявляется кратным числу выходов системы, то есть–целое число. Кроме того, будем также считать, что квадратнаяматрица

, (2.2.1)

где "" ­- означает транспонирование, является неособой, то есть

. (2.2.2)

Переходя к решению данной задачи запишем уравнение выходной переменной для дискретных моментов. В результате получим следующую систему векторных уравнений

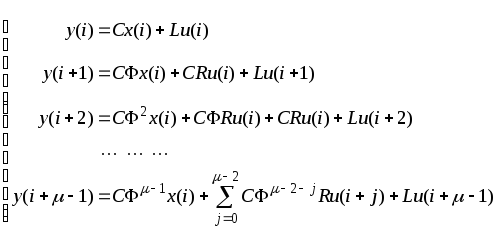
Используя операторное представление с помощью оператора прямого сдвига , запишем эту систему в виде

, (2.2.3)

где матрица определяется на основе блочной формы (2.2.1), а операторные матрицыи, размеровисоответственно, представляются соотношениями

.

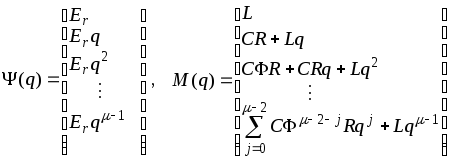Учитывая условие (2.2.2), из (2.2.3) можно определить

. (2.2.4)

Запишем теперь уравнение выходной переменной для момента. С использованием операторного представления будем иметь

.

Подставляя в это соотношение выражение для из (2.2.4) и приводя подобные, получим

.

Обозначая

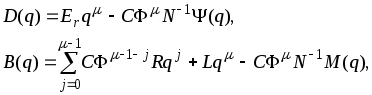(2.2.5)

получим окончательно представление дискретной системы (2.1.10) в операторной форме "вход-выход" (2.1.13).

Анализируя матричные операторные полиномы (2.2.5) можно заключить, что степени этих полиномов совпадают () тогда и только тогда, когда. В противном случае, степень полиномапо крайней мере на единицу меньше, то есть. Отметим также, что в частном случае, когда система имеет скалярный выход (), степень полиномасовпадает с размерностью системы, то есть, а сам полином становится скалярным, превращаясь в характеристический полином.

Переход от формы "вход-выход" к форме Коши.Рассматривая возможность решения данной задачи, прежде всего отметим, что такой переход является неоднозначным, и матрицымодели (2.1.10), являющиеся результатом этого перехода, зависят от выбора переменных состояния системы. В связи с этим, для представления дискретной системы в форме Коши по уравнениям "вход-выход" целесообразно использовать так называемые канонические переменные состояния, которые позволяют представить дискретную систему в одной из канонических форм. Среди таких канонических представлений (аналогично непрерывным системам[10])наиболее часто используют форму Люэнбергера (идентификационное каноническое представление) и форму Фробениуса (представление с помощью фазовых переменных). Рассмотрим, например, переход от формы "вход-выход" (2.1.11) к форме Люэнбергера. При этом будем полагать, что матрица(матричный коэффициент при старшей степени в левой части операторного уравнения (2.1.13)) является единичной, то есть. Если это не так, то умножением уравнения (2.1.11) слева на(эта матрица предполагается неособой) всегда можно добиться требуемого свойства. Кроме того, для определённости положим, что. Заметим также, что если, то общая размерность системы определится как. Тогда для выбора переменных состояния формы Люэнбергера можно использовать следующий алгоритм. Обозначим вектор состояний искомой модели через, и разобьём этот вектор на-мерных векторов, каждый из которых будем выбирать по формулам

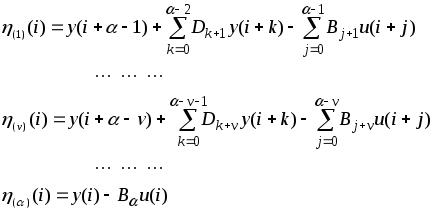
Если теперь записать эти соотношения для момента , то после преобразований можно получить

,

.

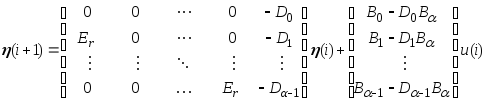Полученные уравнения представляют (при ) дискретную систему в форме Коши. Сравнивая эти уравнения с (2.1.10) заключаем, что матрицыиданной модели имеют каноническую структуру Люэнбергера[10],, а-ый блок матрицыопределяется как (). Таким образом, если дискретная система представлена матричным уравнением "вход-выход" (2.1.11), в котором, то переход от этого уравнения к форме Коши (с использованием канонического представления Люэнбергера) может быть произведён без каких-либо вычислений. Заметим при этом, что если система имеет скалярный выход (), то матрицы() превращаются в скалярные коэффициенты, являющиеся коэффициентами характеристического полинома данной системы.

Переход к форме Коши с использованием канонического представления Фробениуса для общего случая многомерной системы оказывается достаточно сложным. Однако, если система имеет один вход и один выход (), то такой переход также не вызывает каких-либо затруднений. Читателю предлагается самостоятельно убедиться (при этом можно использовать тот же подход, что и в непрерывных системах[10]) в том, что если дискретная система со скалярным входом и выходом представляется в форме "вход-выход" уравнением

,

где (),() – некоторые числа, то соответствующая модель этой системы в форме Коши, записанная в канонической форме Фробениуса, имеет вид

,

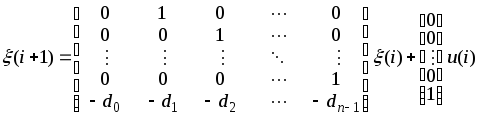
где –вектор дискретных состояний системы, компоненты которого удовлетворяют условиям. По аналогии с непрерывными системами такие переменные состояния дискретных систем называются фазовыми переменными.