2.5. Модели цифровых регуляторов

Регулятор в форме Коши. Рассмотрим систему управления с БЦВМ в контуре. Пусть алгоритм управления, реализуемый в БЦВМ, каким-либо образом определен. Очевидно, что в общем случае этот алгоритм описывается разностными уравнениями, которые будут представлять модель цифрового регулятора. Отметим, что многие из современных методов синтеза дискретных систем[5–­8]ориентированы на представление объекта в форме Коши, что определяет и форму представления модели регулятора, которая в этом случае запишется в виде

(2.5.1)

где - вектор дискретных состояний регулятора;- вектор измеряемых выходов объекта, оцифрованных в моменты(входы регулятора);- вектор дискретных управлений (выходы регулятора);,,,- соответствующих размеров матрицы параметров регулятора (как правило, числовые).

Для реализация алгоритма управления (2.5.1) необходимо задать вектор начальных состояний регулятора , которые обычно принимаются нулевыми, то есть

. (2.5.2)

При этом в соответствии с (2.5.1), одновременно с управлением для-го такта вычисляется и вектор состояний, который должен быть сохранен в оперативной памяти, для соответствующих вычислений на следующем-ом такте.

Регулятор в форме "вход-выход". В некоторых случаях решением задачи синтеза являются разностные уравнения регулятора в форме "вход-выход"[7]. Более того, как будет показано ниже, даже если регулятор получен в форме Коши (2.5.1), то его целесообразно представить в форме "вход-выход", так как при этом уменьшается объем вычислений, которые необходимо производить в БЦВМ для реализации алгоритма управления. В этом случае векторно-матричное уравнение регулятора запишется в виде

, (2.5.3)

где и–матрицы параметров (как правило, числовые) размеромисоответственно. Отметим, что если результатом решения задачи синтеза является модель регулятора в форме Коши (2.5.1), то переход к форме "вход-выход" (2.5.3) может быть осуществлен по алгоритму, аналогичному тому, который был рассмотрен в разделе 2.2. При этом,если размерность регулятора (2.5.1)удовлетворяет условию, где- целое число, то матрицаэтого регулятора, представленного в форме вход-выход (2.5.3), будет единичной.

Полагая для простоты дальнейшего изложения, что последнее условие выполняется, запишем модель (2.5.3) в операторной форме

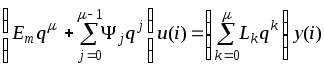, (2.5.4)

где - оператор прямого сдвига.

Особенностью уравнения (2.5.3) и его операторного представления (2.3.4) является то, что эти уравнения содержат решетчатые функции и, которые определяют будущие значения управлений и измеряемых переменных. Это обстоятельство порождает некоторые неудобства при реализации алгоритма управления в БЦВМ. В связи с этим модель регулятора необходимо представить в эквивалентном виде с использованием оператора обратного сдвига. Формально такой переход можно осуществить путем деления обеих частей уравнения (2.5.4) на. В результате получим следующее уравнение

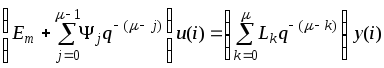. (2.5.5)

Переобозначим матрицы и, входящие в это уравнение следующим образом

.

Тогда, если в (2.5.5) снова перейти к временной форме представления, то нетрудно получить

(2.5.6)

Это соотношение представляет собой алгоритм вычисления управляющего воздействия на текущем -ом такте. Причем как следует из (2.5.6) для этого необходимо, помимо текущих измерений, иметь в оперативной памяти БЦВМ значения измеряемых переменных и управлений из предыдущихтактов.

Отметим, что для реализации алгоритма управления (2.5.6) необходимо задать значения переменных идля. Эти значения, которые мы будем обозначать как начальные условия, обычно принимаются нулевыми, то есть

(2.5.7)

Можно показать, что если для реализации одного и того же регулятора используется модель в форме Коши (2.5.1) с нулевым начальным состоянием (2.5.2), либо алгоритм (2.5.6) с нулевыми начальными условиями (2.5.7), то решения разностных уравнений, описывающих поведение замкнутой системы (относительно вектора состояний объекта) будут тождественно совпадать.

Оценка вычислительной сложности.Для реализации в БЦВМ регулятора, представленного моделью в форме Коши (2.5.1), либо алгоритмом (2.5.6), основанным на форме "вход-выход", необходимо осуществлять операции сложения, умноженияи присвоения. Общее число таких операций определяет процессорную загрузку БЦВМ, и в конечном итоге позволяет установить минимально необходимый период дискретности выдачи управлений, так как все вычисления связанные с реализацией регулятора должны производится в реальном времени.

Приведем сравнительную оценку вычислительной сложности алгоритмов управления, представленных в форме (2.5.1) либо в форме (2.5.6). При этом будем считать, что уравнения (2.5.1) либо (2.5.6) представляют в разных формах один и тот же регулятор, размерность которого удовлетворяет условию .

Для решения данной задачи произведем формальный подсчет числа операций различного типа, которые необходимо произвести на каждом такте для вычисления управления по уравнениям (2.5.1), либо (2.5.6).Результаты этих подсчетов (для ) сведены в табл. 2.1, в которой приводятся также сравнительные оценки числа операций (последняя графа).

Таблица 2.1.

Тип	Число операций на каждом такте		Разность числа операций
операций	Ф. Коши	"вход-выход"
=

Отметим, что при составлении данной таблицы рассматривался случай, когда все элементы матриц, входящих в (2.5.1) либо в (2.5.6) являются ненулевыми. Если же некоторые из элементов этих матриц нулевые, то число операций уменьшается. Отметим также, что при подсчете числа операций присвоения учтены операции, связанные с переобозначением тех переменных текущего такта, которые используются на следующем такте.

Из приведенной таблицы следует, что для реализации закона управления по уравнению (2.5.6), основанному на форме "вход-выход", требуется (при ) значительно меньше операций всех типов. Таким образом модель регулятора, представленная в виде (2.5.5), является наиболее предпочтительной.