2.4. Дискретная модель непрерывного объекта в системе управления с бцвм в контуре

Предварительные замечания.Рассмотрим многомерную систему автоматического управления, где в качестве регулятора используется БЦВМ, связанная с непрерывным объектом с помощью ЦАП и АЦП (рис.1.4). Будем считать, что измеряемый векторный выход объектаквантуется с помощью АЦП в моментытак, что на входе БЦВМ действует векторная решётчатая функция. В БЦВМ реализуется определённый алгоритм управления и на её выходе формируется последовательность дискретных значений управляющих воздействий, которую также можно рассматривать как векторную решётчатую функцию. Здесь для простоты положим, что разрядность ЦАП и АЦП достаточно высока, так что эффектом квантования по уровню можно пренебречь.

Пусть непрерывный объект представляется дифференциальными уравнениями в форме Коши

(2.4.1)

где –числовые матрицы соответствующих размеров.

Будем считать, что ЦАП и АЦП работают синхронно (с одинаковым периодом), но не синфазно, и пусть выдача рассчитанных управлений производится с задержкой на, где–относительное запаздывание, так что на ЦАП поступает смещённая решётчатая функция. Таким образом, эквивалентная схема принимает вид рис.2.5.

Рис. 2.5.

Очевидно, что непрерывный объект управления (2.4.1) совместно с ЦАП, АЦП и звеном задержки можно рассматривать как некоторую эквивалентную дискретную систему, на входе и выходе которой действуют решётчатые функцииисоответственно. Как и в случае импульсных систем, разностные уравнения, описывающие эту систему, должны быть такими, чтобы их решения относительно переменных выхода и состояний совпадали прис соответствующими непрерывными функциями. Эти разностные уравнения как раз и будут являться дискретной моделью непрерывного объекта в системе управления с БЦВМ в контуре. Причём, эта модель, очевидно, будет зависеть от способа восстановления непрерывного процессапо его дискретам.

Применение экстраполяции нулевого порядка.Пусть операция ЦА-преобразования сопровождается формированием управленияметодом фиксации на период (экстраполяция нулевого порядка). Тогда функциябудет кусочно-постоянной (рис.2.6), удовлетворяющей условию

. (2.4.2)

Для определения дискретной модели объекта (2.4.1) при условии (2.4.2) рассмотрим -ый интервал дискретности.

Рис. 2.6.

В соответствии с рис.2.6, этот интервал можно разбить на два под-интервала. На первом подинтервале, когда, на объект действует постоянное управление, а на втором – постоянное управление. Учитывая сказанное и используя формулу Коши (2.3.3), определим состояниев конце интервала по известному состояниюв начале интервала. Будем иметь

Преобразуем это выражение, используя для первого интеграла замену , а для второго –. Тогда после преобразований и перехода к решётчатым функциям получим

Обозначим

(2.4.3)

и учтём, что квантование выхода производится в моменты. Тогда окончательно, искомая дискретная модель примет вид

. (2.4.4)

Анализируя формулы (2.4.3), заметим, что матрицы изависят от величины запаздывания. Так, если(запаздывание отсутствует), тои мы получим дискретную модель непрерывного объекта без запаздывания. Если же, то, и тогда уравнения (2.4.4) будут представлять дискретную модель с "чистым" запаздыванием на один такт.

Отметим также, что при разностные уравнения (2.4.4) формально не являются уравнениями в форме Коши, так как в правой части первого уравнения присутствует переменная, сдвинутая на один такт по отношению к другим. Для устранения этого "недостатка" введем вектор дополнительных состояний , . Тогда нетрудно показать, что расширенная дискретная модель с вектором состояний , представится в следующем эквивалентном виде

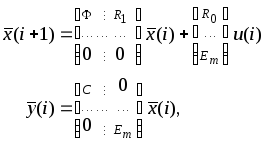(2.4.5)

где - новый вектор измеряемых переменных объекта, расширенных за счет управлений из предыдущего такта.

Таким образом наличие запаздывания привело к увеличению размерности дискретной модели по сравнению с размерностью непрерывного объекта. Это позволяет учесть запаздывание при синтезе алгоритмов работы БЦВМ (дискретных регуляторов), так как формально уравнения (2.4.5) представляют дискретную модель объекта без запаздывания, но повышенной размерности.

Применение экстраполяторов -го порядка. При рассмотрении этого вопроса для простоты ограничимся случаем . Кроме того, также для простоты, будем считать, что управлениеявляется скалярным (). Тогда, если для реализации этого управления используется метод экстраполяции-го порядка, то на интервалеуправлениебудет определяться выражением (1.4.10), то есть

, (2.4.6)

где производные () могут быть вычислены по дискретам,в соответствии с алгоритмом (1.4.16).

Переходя к определению дискретной модели непрерывного объекта (2.4.1) запишем состояние этого объекта в конце-го интервала дискретности по известному состояниюв начале интервала. Используя формулу Коши, будем иметь

.

Подставляя (2.4.6) и производя замену , после преобразований и перехода к решетчатым функциям, получим

. (2.4.7)

Здесь учтено, что значения производных остаются постоянными в течение каждого интервала дискретности. Обозначим

,,.

Тогда (2.4.7) примет вид

.

Введем матрицу . Тогда, если использовать обозначение (1.4.12) для вектора, получим

.

Используя далее алгоритм вычисления производных (1.4.16) будем иметь

, (2.4.8)

где - определяется выражением (1.4.14), а- обозначает-мерный вектор (1.4.12), составленный из дискрет.

Обозначим столбцы матрицы через. Тогда учитывая структуру вектора, окончательно получим искомую дискретную модель

. (2.4.9)

Заметим, что несмотря на то, что по предположению управляющее воздействие формируется без задержки по отношению к моментам съема информации, дискретная модель (2.4.9) содержит запаздывания по управлению натактов одновременно. Как уже отмечалось в разделе 1.4, этот факт обусловлен использованием для формирования управленияэкстраполяции-го порядка.

Запишем полученную модель в эквивалентной форме с помощью расширенного состояния. Для этого введем вспомогательные переменные

.

Очевидно, что в этом случае

.

Тогда, если ввести вектор расширенного состояния

а также новый вектор измеряемых переменных

,

расширенный за счет управлений из предыдущих тактов, то (2.4.9) можно представить в следующем эквивалентном виде

, (2.4.10)

где ,,- матрицы размеров,,соответственно, имеющие следующую блочную структуру

, ,. (2.4.11)

Уравнения (2.4.10) представляют дискретную модель непрерывного объекта в системе управления с БЦВМ и экстраполятором -го порядка. Эта модель составлена для скалярного управления, и учет экстраполятора привел к тому, что ее размерность увеличилась напо сравнению с размерностью непрерывного объекта. Очевидно, что если рассматривать случай векторного управления, то формально дискретная модель (2.4.10) останется без изменения, но вводимые дополнительные переменныестанут векторными и общая размерность модели составит.