2.3. Дискретные модели непрерывных систем с импульсными элементами

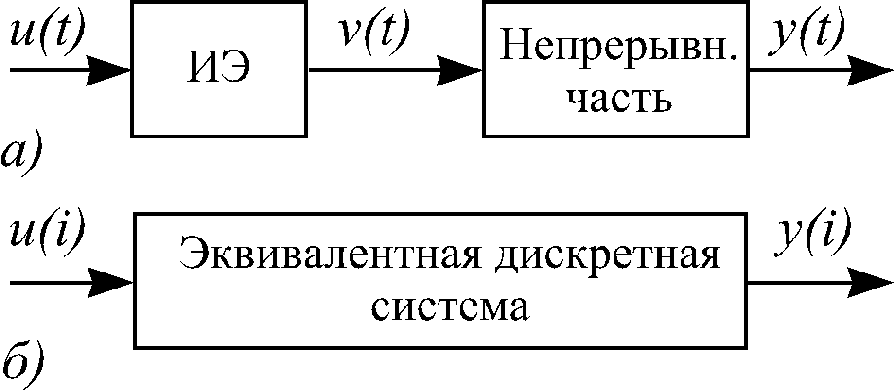
Понятие дискретной модели импульсной системы.Рассмотрим систему автоматического управления, содержащую один или несколько импульсных элементов. Тогда по числу этих элементов всю систему можно разбить на пары – импульсный элемент + непрерывная часть (рис.2.3,а). Импульсный элемент (ИЭ) преобразует непрерывный процессна его входе в последовательность импульсов, следующих с одинаковым шагом, передавая информацию о непрерывном процесселибо в высоте (АИМ), либо в ширине (ШИМ) этих импульсов. Таким образом, входной непрерывный сигналквантуется в моменты, и следовательно, для него можно построить соответствующую решётчатую функцию.

Пусть выходной сигнал непрерывной части также квантуется (например, с помощью последующих импульсных элементов) в те же моменты времени. Тогда для этого сигнала также можно построить решётчатую функцию. Очевидно, что при указанных условиях для описания процессов протекающих в данной системе целесообразно использовать аппарат решётчатых функций, заменив непрерывную часть системы с импульсным элементом на входе некоторой эквивалентной дискретной системой (рис.2.3, б), на входе и выходе которой определены соответствующие решётчатые функциии. Модель этой дискретной системы представляется разностными уравнениями. Причём, эти уравнения должны быть такими, чтобы прииз их решений однозначно вытекало. Более того, еслиобозначает вектор состояний непрерывной системы, то для соответствующей эквивалентной дискретной системы вектор состоянийдолжен удовлетворять условию. Данные разностные уравнения, представляющие эквивалентную дискретную систему и удовлетворяющие указанным условиям, называются дискретной моделью непрерывной системы с импульсным элементом (импульсной системы).

Рис. 2.3.

Дискретная модель импульсной системы с АИМ.Пусть импульсный элемент на входе непрерывной части (рис.2.3, а) реализует амлитудно-импульсную модуляцию с помощью прямоугольных импульсов, следующих с периодоми со скважностью(рис.1.2). Тогда, полагая для простоты, аналогично (1.2.3) запишем

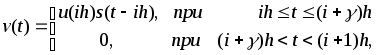(2.3.1)

где –одиночный прямоугольный импульс единичной амплитуды длительности, действующий в момент.

Пусть непрерывная часть системы представляется линейными дифференциальными уравнениями в форме Коши

(2.3.2)

где –матрицы чисел соответствующих размеров. Причём решение этих уравнений относительноопределяется формулой

. (2.3.3)

Рассмотрим -ый интервал дискретности, который с учётом (2.3.1) можно разбить на два подинтервалаи. На первом подинтервале на непрерывную часть действует постоянный сигнал, а на втором. Тогда, если принять, то в соответствии с (2.3.3) состояние непрерывной части в конце интервала, то есть при, определится выражением

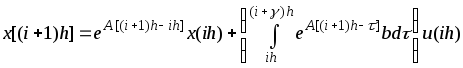. (2.3.4)

Преобразуем второе слагаемое правой части, используя замену . Тогда, если учесть, что при, а при, и кроме того,, то (2.3.4) можно переписать в виде

. (2.3.5)

Обозначим

. (2.3.6)

Тогда, переходя в (2.3.5) к решётчатым функциям и учитывая, что квантование выходного сигнала производится в те же моменты времени, окончательно получим дискретную модель импульсной системы с АИМ

(2.3.7)

где – та же, что и в (2.3.2), а матрицыиопределяются соотношениями (2.3.6).

Аналогично может быть определена дискретная модель импульсной системы с АИМ, реализуемой с помощью непрямоугольных импульсов.

Дискретная модель импульсной системы с ШИМ.Пусть импульсный элемент на входе непрерывной части (рис.2.3, а) реализует широтно-импульсную модуляцию. Для определённости положим, что имеет место ШИМ с помощью разнополярных прямоугольных импульсов (рис.1.3, б), следующих с периодоми имеющих скважность положительных импульсов, определяемую соотношением

, (2.3.8)

где – коэффициент передачи импульсного элемента; – квантованный в моментывходной сигнал импульсного элемента. При этом для его выходного сигналааналогично (1.2.4) можно записать

, (2.3.9)

где –амплитуда импульсов.

Переходя к нахождению дискретной модели данной импульсной системы, рассмотрим -ый интервал дискретности, который в соответствии с (2.3.9) можно разбить на два подинтервалаи. На первом подинтервале на непрерывную часть (2.3.2) действует положительный постоянный сигнал, а на втором – отрицательный, то есть. Используя формулу Коши (2.3.3) найдём состояние непрерывной частив конце интервала по известному состояниюв начале этого интервала. Учитывая сделанные замечания, будем иметь

. (2.3.10)

Преобразуем выражение в фигурных скобках, используя для первого интеграла замену , а для второго. Тогда после перехода к решётчатым функциям (2.3.10) принимает вид

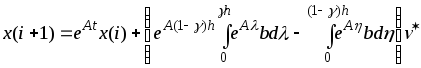. (2.3.11)

В этом уравнении выражение в фигурных скобках нелинейно зависит от скважности , которая в свою очередь, в соответствии с (2.3.8), пропорциональна решётчатой функции входа. Таким образом, если обозначить

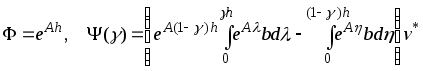
и учесть, что квантование выхода осуществляется в те же моменты времени, то окончательно дискретная модель системы с ШИМ примет вид

(2.3.12)

где – та же, что и в (2.3.2). Аналогично можно получить дискретную модель импульсной системы с ШИМ, реализуемой с помощью непрямоугольных или с помощью полярных импульсов (рис.1.3, а).

Заметим, что несмотря на то, что непрерывная часть системы описывается линейными уравнениями, её дискретная модель оказалась нелинейной относительно входного воздействия.

Проведём линеаризацию (2.3.12) относительно некоторого режима, определяемого входным воздействием . Пусть для определённости, тогда в соответствии с (2.3.8), а. Разложим функциюв ряд Тейлора в окрестности. Формальное разложение этой функции будет иметь вид

, (2.3.13)

где –это члены разложения высших порядков малости, а векторная величина, которую будем обозначать как, определится соотношением

. (2.3.14)

Обозначим

(2.3.15)

и найдём векторную функцию

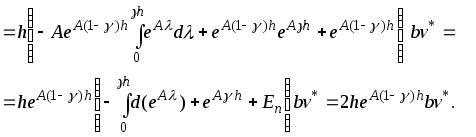
Подставляя , получим для

. (2.3.16)

Таким образом с учётом (2.3.15) нелинейная функция (2.3.13) может быть представлена в виде

,

где иопределяются формулами (2.3.14) и (2.3.16) соответственно.

Если теперь отбросить члены разложения высших порядков малости, то окончательно линеаризованная дискретная модель импульсной системы с ШИМ принимает вид

(2.3.17)

Эта модель устанавливает, в частности, одну особенность импульсных систем с ШИМ, которая заключается в том, что даже при отсутствии входного воздействия (), установившаяся решётчатая функция выходабудет отличной от нуля. Формально это объясняется наличием в первом уравнении (2.3.17) постоянного вектора, играющего роль внешнего возмущения. Физически этот эффект можно объяснить на следующем простом примере.

Пусть непрерывная часть системы описывается дифференциальным уравнением первого порядка

,

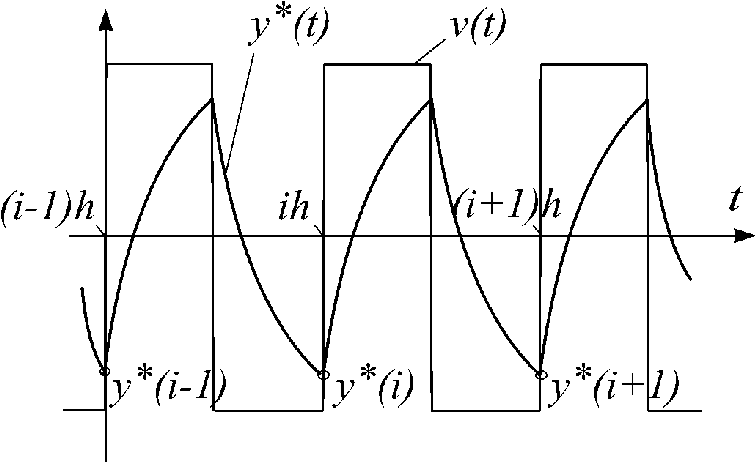
где –постоянная времени, которую будем считать соизмеримой с периодом дискретности. Тогда присигнална выходе импульсного элемента (на входе непрерывной части) будет представляться последовательностью разнополярных прямоугольных импульсов длительности, а установившаяся реакция непрерывной части на такое воздействие представится периодической функциейс нулевым средним и состоящей из кусков экспонент (рис.2.4). Квантование этой функции в моментыдаёт решётчатую функцию, которая оказывается отличной от нуля.

Рис. 2.4.

Из приведённого примера, а также непосредственно из формулы (2.3.14) следует, что, если, то есть, при достаточно большой частоте квантования отрицательные эффекты, связанные с применением ШИМ исчезают. В связи с этим в практических задачах широтно-импульсную модуляцию всегда реализуют с высокой частотой, когда период дискретностиоказывается значительно меньше (на несколько порядков) постоянных времени непрерывной части. В этом случае непрерывная часть реагирует на среднее значение импульсного сигнала, которое пристановится непрерывной функцией, и эффект квантования по времени пропадает. Этим же объясняется и тот факт, что при использовании ШИМ с высокой частотой систему считают непрерывной и дискретную модель этой системы не используют.