2. 3.4. Структурные схемы дискретных систем

Особенность составления и преобразования структурных схем непрерывно-дискретных систем.Структурные схемы дискретных систем представляются соединением дискретных звеньев, для каждого из которых определена–передаточная функция. Особенность составления структурных схем непрерывно-дискретных систем как раз и проявляется в разбиении системы на дискретные звенья и связана с наличием в системе импульсных и квантующих элементов. При этом в системе управления с БЦВМ в контуре роль импульсных элементов выполняют ЦАП, а квантующими элементами являются АЦП.

Рис. 3.3.

Число дискретных звеньев в непрерывно-дискретной системе определяется числом пар – импульсный элемент + непрерывная часть. Так, если какая-то непрерывная часть системы содержит на входе импульсный элемент, работающий с некоторым периодом дискретности, и выход этой непрерывной части квантуется (в общем случае со сдвигом) с тем же периодом, то данная часть системы будет содержать одно дискретное звено (рис.3.3). 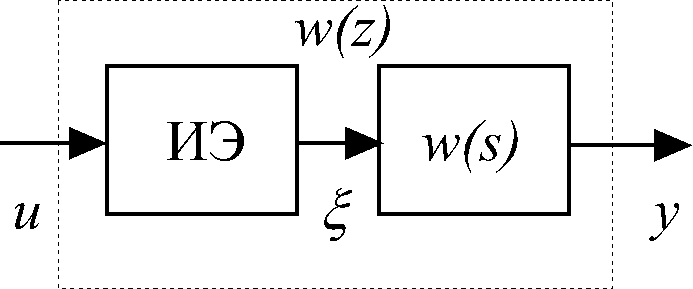При этом, если импульсный элемент реализует амплитудно-импульсную модуляцию прямоугольными импульсами со скважностью(ЦАП является экстраполятором нулевого порядка), то –передаточная функция данного дискретного звена может быть определена по передаточной функции непрерывной частипо формуле (3.3.14).

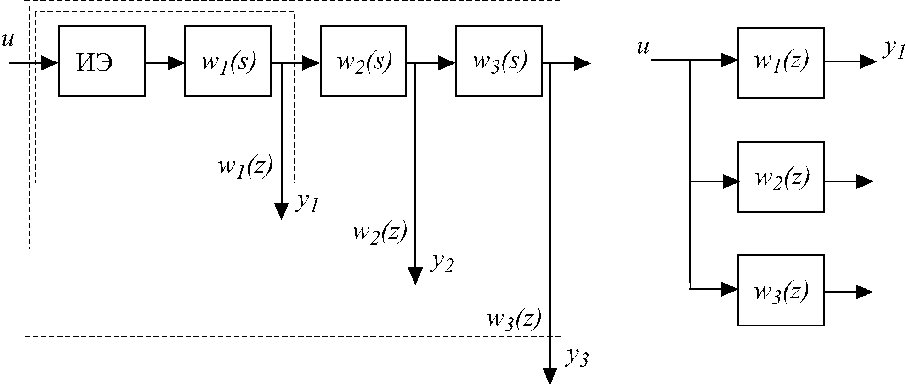
Если система содержит несколько импульсных элементов и непрерывная часть, соответствующая какому-либо импульсному элементу имеет квантуемый выход (например, с помощью последующих импульсных элементов), то данная система может быть представлена соединением соответствующего числа дискретных звеньев. При этом если непрерывная часть, соответствующая какому-либо импульсному элементу, имеет несколько квантуемых выходов (рис.3.4, а), то эта часть системы также представится несколькими дискретными звеньями по числу квантуемых выходов (рис.3.4, б). Причём, –передаточные функции дискретных звеньев будут определяться парами – импульсный элемент + непрерывная часть по соответствующему выходу.

а)б)

Рис. 3.4.

Отметим, что если непрерывная часть с одним импульсным элементом на входе представляется последовательным соединением более элементарных звеньев, то есть, то соответствующее дискретное звено нельзя представить последовательным соединением дискретных звеньев, являющихся результатом дискретизации отдельных непрерывных звеньев, то есть, где–результат формального применения формулы (3.3.14) к передаточной функции.

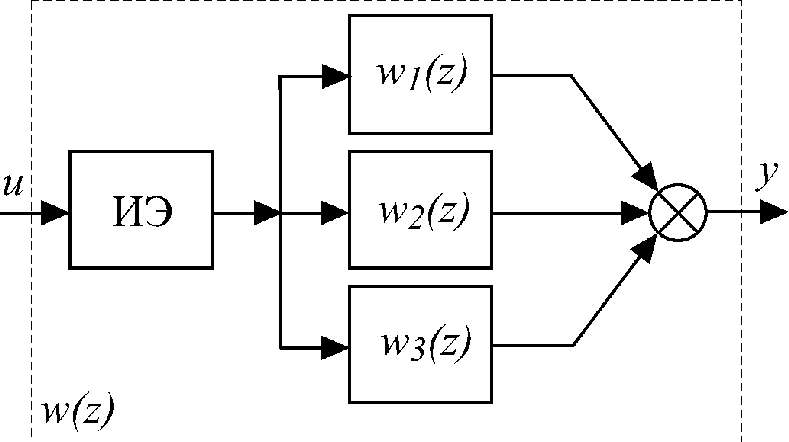
С другой стороны, если непрерывная часть, соответствующая какому-либо импульсному элементу представляется параллельным соединением звеньев с общим импульсным элементом на входе (рис.3.5), то для нахождения общей –передаточной функции соответствующего дискретного звена можно использовать свойство параллельного соединения. Другими словами, если для непрерывной части имеет место, то для соответствующего дискретного звена, где–могут быть получены по передаточным функциям.

Рис. 3.5.

После того как с учётом отмеченных особенностей система разбита на дискретные звенья и для каждого дискретного звена определена его–передаточная функция, вступают в силу обычные правила преобразования структурных схем, такие же, как и для непрерывных систем. Так, для последовательного(рис.3.6, а)и параллельного (рис.3.6, б) соединения дискретных звеньев с передаточными функциямиможно соответственно записать

,.

Для соединения звеньев с обратной связью (рис.3.6, в) имеет место

,

где "+" для отрицательной обратной связи и "–" для положительной.

Рис. 3.6.

Также как и в непрерывных системах, в структурных схемах дискретных систем можно переносить точки съёма или суммирования. Так например, структурная схема рис.3.4,б может быть преобразована в форму последовательного соединения (рис.3.7), что в некоторых случаях даёт более наглядное представление системы.

Рис. 3.7.

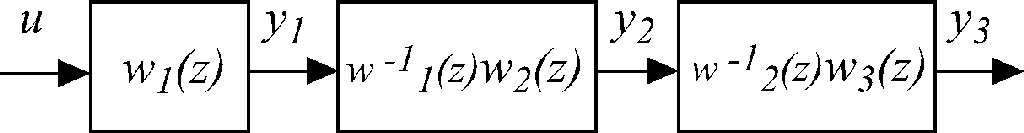
Пример составления структурной схемы системы управления с БЦВМ в контуре.В качестве примера рассмотрим цифровую следящую систему, принципиально-функциональная схема которой представлена на рис.3.8. Объектом управления в этой системе является двигатель (Д) с усилителем мощности (УМ). Вал двигателя через редуктор соединён с нагрузкой (Н), которая создаёт на валу приведённый момент сопротивления. В качестве измерителей используются: сельсинная пара (СД-СП) – для измерения рассогласования, и тахогенератор (ТГ) – для измерения скорости вращения вала двигателя.

Алгоритм управления этой системой реализуется в БЦВМ, связанной с объектом управления и с измерительными устройствами через ЦАП и АЦП. В БЦВМ поступает оцифрованная информация о сигналах и. При этом сигналпропорционален рассогласованиюи формируется с помощью фазочувствительного усилителя-выпрямителя (ФЧУВ). Сигналпропорционален скорости вращенияи снимается непосредственно с тахогенератора.

Рис. 3.8.

Прежде чем перейти к составлению структурной схемы данной непрерывно-дискретной системы приведём математическую модель непрерывной части этой системы, которая образована объектом управления и измерительными устройствами. При этом для простоты будем считать, что ФЧУВ и УМ являются безынерционными элементами, а индуктивность обмотки двигателя пренебрежимо мала. Тогда, используя математическую модель двигателя постоянного тока[10], для объекта управления (Д+УМ+редуктор) можно записать

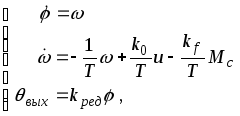(3.4.1)

где –электромеханическая постоянная времени двигателя;–статические коэффициенты передачи объекта по управлению и внешнему возмущению соответственно, причёмвключает в себя коэффициент передачи УМ;–коэффициент передачи редуктора.

Для измерительных устройств будем иметь

(3.4.2)

где –коэффициенты передачи измерителей, причёмвключает коэффициент передачи ФЧУВ.

Не раскрывая пока содержания реализуемого в БЦВМ закона управления приведём структурную схему данной системы с использованием передаточных функций непрерывных элементов. Для этого перейдём в (3.4.1) и (3.4.2) к преобразованиям по Лапласу и запишем изображения выходных переменных объекта и измерительных устройств

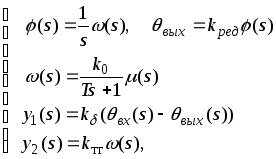(3.4.3)

где –изображение по Лапласу вспомогательной переменной, определяемой соотношением

. (3.4.4)

По уравнениям (3.4.3), (3.4.4) нетрудно составить структурную схему, которая представлена на рис.3.9.

Рис. 3.9.

Перейдём теперь к решению основной задачи – составлению структурной схемы данной непрерывно-дискретной системы с использованием дискретных моделей и–передаточных функций. Для этого систему надо разбить на эквивалентные дискретные звенья и определить для них–передаточные функции. При этом, в соответствии с результатами раздела 3.3, возможны два подхода к решению данной задачи. Один из них связан с нахождением дискретной модели непрерывной части в виде разностных уравнений. Далее эти разностные уравнения записываются в Z–изображениях и определяются–передаточные функции эквивалентных дискретных звеньев. В данном подходе учёт особенностей разбиения системы на такие звенья заложен в самом методе решения задачи, и в этом смысле является более универсальным. Другой метод связан с определением–передаточных функций эквивалентных дискретных звеньев непосредственно по передаточным функциям непрерывных элементов. При использовании этого подхода необходимо учитывать все особенности, связанные с наличием в системе импульсных (ЦАП) и квантующих (АЦП) элементов.

Рассмотрим оба подхода. При этом будем считать, что ЦАП и АЦП работают синхронно с периодом дискретности и ЦАП является экстраполятором нулевого порядка. Пусть также выдача управления производится с задержкой на один такт дискретности по отношению к моментам съёма информации, а момент сопротивленияявляется медленно изменяющейся функцией, так что в пределах каждого такта дискретности можно принять. Тогда, если учесть, что с введением вспомогательной переменной (3.4.4) уравнения непрерывного объекта (3.4.1) формально представляются в виде (3.3.18) (пример из предыдущего раздела), то дискретную модель непрерывной части системы можно представить следующими разностными уравнениями

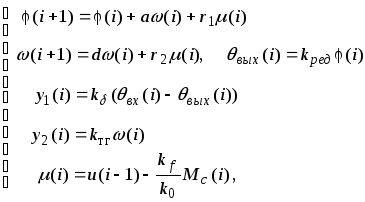(3.4.5)

где параметры определяются из формул (3.3.19) прии имеют вид

.

Отметим, что в последнем уравнении системы (3.4.5) учтено запаздывание по управлению на один такт.

Переходя в уравнениях (3.4.5) к Z–изображениям, запишем изображения выходных переменных объекта и измерителей. После несложных преобразований будем иметь

(3.4.6)

где . Первые два соотношения в этих уравнениях содержат–передаточные функции эквивалентных дискретных звеньев, с помощью которых теперь представляется непрерывный объект, то есть

.

Эти же передаточные функции можно получить на основе второго подхода непосредственно по структурной схеме рис.3.9 с использованием передаточных функций непрерывных элементов. При этом

.

Пусть алгоритм работы БЦВМ представляется в форме "вход-выход" следующим разностным уравнением

,

где –некоторые числовые параметры. Переходя в этом уравнении кZ–изображениям, запишем выражение для выходной переменной дискретного регулятора

. (3.4.7)

Рис. 3.10.

Добавляя это соотношение к уравнениям (3.4.6) получим полное описание рассматриваемой системы вZ–изображениях выходных переменных дискретных звеньев. Теперь по этим уравнениям легко составляется структурная схема системы, которая представлена на рис.3.10. Используя обычные методы преобразования структурных схем (те же, что и для непрерывных систем), на основе этой структурной схемы можно определить любые другие передаточные функции дискретной системы (замкнутой, разомкнутой и т.д.).

Отметим, что алгоритм управления, реализуемый в БЦВМ, который в Z–изображениях представляется соотношением (3.4.7), на структурной схеме отмечен пунктиром. Остальные элементы структурной схемы-это эквивалентные дискретные звенья, моделирующие непрерывную часть системы.

2. Анализ дискретных систем в частотной области

Реакция дискретной системы на гармоническое воздействие.Рассмотрим линейную дискретную систему с одним входом и одним выходом, представленную следующими разностными уравнениями

(3.5.1)

где - вектор состояний,- переменные входа и выхода,,,- числовые матрицы соответствующих размеров.

Определим установившуюся реакцию выхода этой системы на гармоническую решетчатую функцию, в качестве которой для определенности выберем

, (3.5.2)

где - период дискретности,,- частота и амплитуда данного воздействия. Отметим, что воздействие (3.5.2) обладает тем свойством, что если вместо параметраподставить, где- любое целое, то (3.5.2) не изменится. Действительно, с учетом периодичности гармонической функции получим

.

Таким образом решетчатая функция (3.5.2) является периодической не только по аргументу (по дискретному времени), но и по аргументус периодом. Это означает, что при нахождении реакции системы (3.5.1) на гармоническое воздействие (3.5.2) частоту этого воздействиядостаточно выбирать в диапазоне. Отметим, что при теоретических исследованиях часто используют понятие отрицательных частот. Поэтому вместо указанного диапазона следует принять, который очевидно охватывает все возможные частоты гармонических решетчатых функций.

Используя формулу Эйлера, представим воздействие (3.5.2) в виде двух составляющих

(3.5.3)

Тогда установившуюся реакцию выхода дискретной системы (3.5.1) также можно искать в виде двух составляющих

, (3.5.4)

где ,- вынужденные решения разностного уравнения (3.5.1) относительно вектора состояний при соответствующем воздействии из (3.5.3). Будем искать эти вынужденные решения в таком же виде как и сами воздействия (3.5.3). Так дляпримем

, (3.5.5)

где - неизвестная пока векторная функция. Для ее нахождения подставим (3.5.5) в исходное уравнение, в котором вместобудем использовать. Получим

.

Отсюда

,

и, таким образом, с учетом (3.5.5), первая составляющая установившейся реакции выхода определится соотношением

.

Обозначим

, (3.5.6)

тогда последнее выражение запишется в виде

. (3.5.7)

Совершенно аналогично можно определить и вторую составляющую реакции выхода. Она будет иметь вид

. (3.5.8)

Используя понятие модуля и аргумента комплексной функции, запишем (3.5.6) в следующей форме

, (3.5.9)

где

, (3.5.10)

. (3.5.11)

Тогда для установившейся реакции выхода (3.5.4), с учетом (3.5.7), (3.5.8) будем иметь

Применяя теперь снова формулу Эйлера, окончательно получим

. (3.5.12)

Таким образом, при воздействии на линейную дискретную систему гармонической решетчатой функции установившаяся реакция на ее выходе также является гармонической решетчатой функцией той же частоты, но с другой амплитудой и другой фазой. При этом отношение амплитуд выхода и входа есть функция , а сдвиг фаз между выходом и входом совпадает с функцией.

Частотные характеристики дискретных систем.Рассмотрим комплексную функцию, определяемую формулой (3.5.6). Она называется частотной передаточной функцией дискретной системы (3.5.1). Если воспользоваться понятием-передаточной функции этой системы

,

то нетрудно видеть, что характеристика образуется из передаточной функциипутем формальной подстановки

. (3.5.13)

Представим функцию в виде

.

Тогда при изменении частоты в интервале , в комплексной плоскостиполучим некоторую кривую, которая называется годографом амплитудно-фазо-частотной характеристики (АФЧХ) дискретной системы. В силу (3.5.13) эту характеристику можно рассматривать как отображение комплексной плоскостив комплексную плоскость, когда переменнаяизменяется вдоль окружности единичного радиуса,(рис.3.1, б).

Рассмотрим теперь вещественные характеристики и, определяемые формулами (3.5.10) и (3.5.11). Характеристика, представляющая собой зависимость отношения амплитуд гармонических решетчатых функций выхода и входа от частоты входного воздействия, называется амплитудно-частотной характеристикой (АЧХ) дискретной системы. Соответственно характеристика, отражающая зависимость сдвига фаз гармонических решетчатых функций выхода и входа от частоты, называется фазо-частотной характеристикой (ФЧХ). При этом, как следует из (3.5.10), (3.5.11),ианалитически определяются как модуль и аргумент частотной передаточной функции.

Отметим, что характеристики ,ипо построению являются периодическими функциями относительно аргументас периодом. Поэтому при их построении достаточно рассматривать диапазон частот. Практически обычно ограничиваются лишь положительным диапазоном, так как для отрицательных частот данные характеристики ведут себя симметрично. Это нетрудно показать, используя свойства комплексной функции.

Ограниченность частотного диапазона вызывает некоторое неудобство при построении частотных характеристик дискретных систем. Другим более существенным препятствием является довольно сложная зависимость этих характеристик от частоты . В связи с этим в практических задачах, довольно часто, вместо частотных характеристик,ииспользуют, так называемые, псевдочастотные характеристики. Эти характеристики определяются с помощью билинейного преобразования следующего вида

, (3.5.14)

которое часто называют -преобразованием. Оно отображает единичную окружность комплексной плоскостив мнимую ось на комплексной плоскости. Действительно, если, то с использованием формулы Эйлера из (3.5.14) получим

. (3.5.15)

При этом, если частота изменяется отдо, то параметрбудет изменяться отдо. Таким образом (3.5.15) преобразует действительную частотув безразмерный параметр, который называется относительной псевдочастостой.

Часто вместо относительной псевдочастоты используют абсолютную псевдочастоту , которая связана ссоотношением

(3.5.16)

и имеет размерность . Заметим, что при низких частотах, когда, функциюможно приближённо заменить его аргументоми тогда из (3.5.16) следует, что.

Учитывая сказанное, приведём процедуру построения псевдочастнотных характеристик для абсолютной псевдочастоты. Первым шагом в этой процедуре является переход к новой комплексной переменной . Для этого из (3.5.14) выразими подставим в–пере­даточную функцию исследуемой дискретной системы. В результате получим новую дробно-рациональную функцию

,

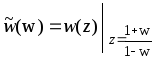в которой затем произведём замену , где. Полученная таким образом комплексная функцияслужит основой для построения псевдочастотных характеристик дискретной системы. Так, приполучим псевдочастотную передаточную функцию, которая в комплексной плоскости представится годографом псевдочастотной АФЧХ. При этом

и

будут представлять псевдочастотные АЧХ и ФЧХ. На основе этих функций можно определить также логарифмические псевдочастотные характеристики и, правила построения которых по передаточной функциите же, что и в непрерывных системах[3].

Частотные свойства непрерывно-дискретных систем.Рассмотрим односвязную непрерывную систему с импульсным элементом на входе. Для определённости будем полагать, что в роли импульсного элемента выступает ЦАП с экстраполяцией нулевого порядка (ЭНП), работающий с периодом, а выход системы квантуется с тем же периодом с помощью АЦП (рис.3.11). Для простоты будем считать, то сдвиг между решётчатыми функциямиина входе и выходе эквивалентной дискретной системы отсутствует.

Рис. 3.11.

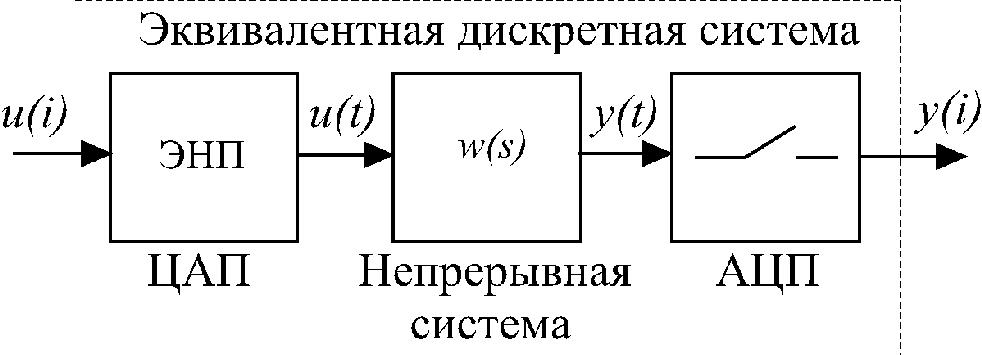
Установим связь между частотными характеристиками непрерывной системы и соответствующей ей эквивалентной дискретной системы. Для этого воспользуемся соотношением (3.1.7), которое устанавливает соответствие между преобразованием Лапласа некоторой непрерывной функции иD–преобразованием соответствующей ей решётчатой функции. По отношению к функциями, обозначающих выходы рассматриваемой системы (рис.3.11), эта связь запишется в виде

, (3.5.17)

где .

Чтобы перейти к передаточным функциям разделим (3.5.17) на , которая представляет собойD–изображение решётчатой функции входа. Тогда получим

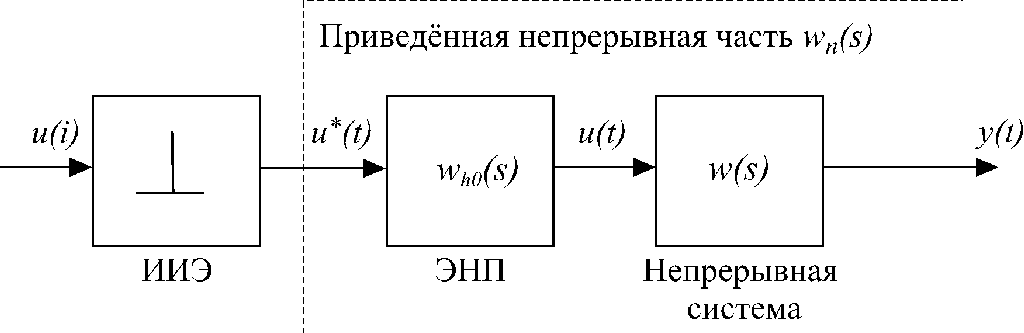
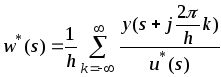, (3.5.18)

где обозначает передаточную функцию эквивалентной дискретной системы, которая, очевидно, может быть получена из её‑передаточной функцииподстановкой.

Отметим, что как показано в разделе 3.1, D–изображениеможно рассматривать как обычное преобразование Лапласа от некоторой вспомогательной функции, образованной последовательностью дельта-функций, взвешенных значениями, то есть. Тогда (3.5.18) можно записать в виде

, (3.5.19)

Рис. 3.12.

гдеобозначает передаточную функцию некоторой приведённой непрерывной части (рис.3.12). Она связывает изображения по Лапласу непрерывного выходаи вспомогательной функции на входе. Заметим, что сигналможно рассматривать как выход некоторого идеального импульсного элемента (ИИЭ), генерирующего с периодом–импульсы, взвешенные значениями, а приведённую непрерывную часть – как последовательное соединение формирователя прямоугольных импульсов (экстраполятора нулевого порядка) и непрерывной системы. При этом очевидно, что

, (3.5.20)

где - обозначает передаточную функцию экстраполятора.

Перейдем в (3.5.19) к частотным передаточным функциям. Заменяя получим

, (3.5.21)

где - частота квантования.

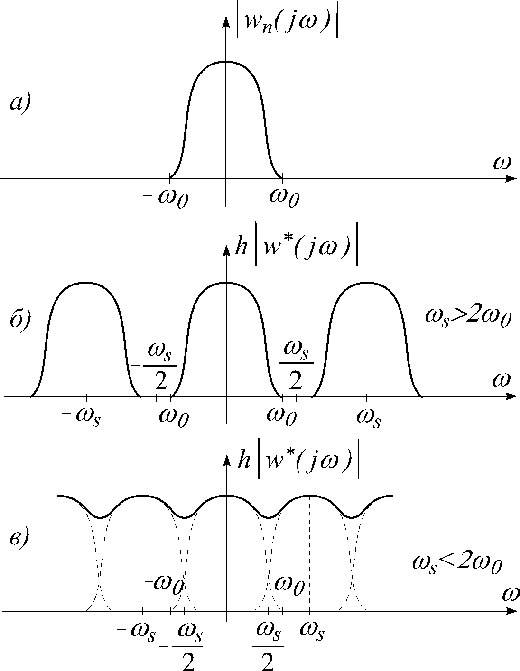
Предположим, что с достаточной для практики точностью можно считать, что частотная характеристика приведенной непрерывной части обращается в ноль начиная с некоторой частоты (рис.3.13, а), то есть

, при.

Тогда, если частоту квантования выбрать из условия, то как следует из (3.5.21), частотные характеристики дискретной системы совпадают в основной полосе частотс частотными характеристиками приведенной непрерывной части с точностью до постоянного множителя(рис.3.13, б). Если же, то частотные характеристики могут существенно отличаться (рис.3.13, в).

Рис. 3.13.

Рассмотрим влияние экстраполятора нулевого порядка на частотные свойства непрерывно-дискретной системы. Для этого определим передаточную функциюэкстраполятора. Как уже отмечалось ранее, эквивалентное представление непрерывно-дискретной системы (рис.3.12) предполагает, что на входе экстраполятора действует вспомогательная функция, состоящая из последовательности-импульсов, взвешенных значениями, то есть

.

На выходе экстраполятора формируется последовательность прямоугольных импульсов с амплитудой и длительностью. Таким образом для выходного сигнала экстраполятора можно записать

,

где - единичная ступенчатая функция.

Определяя преобразования по Лапласу для сигналов и, будем иметь

Взяв отношение этих изображений, окончательно получим

. (3.5.22)

Для оценки частотных свойств экстраполятора перейдем к частотной передаточной функции. Подставляя в (3.5.22) и применяя формулу Эйлера запишем

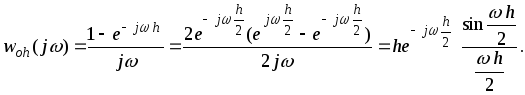
Если учесть, что , то последнее выражение можно преобразовать к виду

.

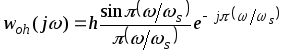Модуль и аргумент этой комплексной функции определяется следующим образом

(3.5.23)

где - целая часть отношения частот.

Графики функций (3.5.23) представлены на рис.3.14. Из этих графиков в частности следует, что на частотах экстраполятор почти не вносит искажений сигнала, и следовательно для этой полосы частот, с учетом (3.5.20), приближенно можно считать, что , то есть

при частотные характеристики непрерывной системы и приведенной непрерывной части практически будут отличаться лишь постоянным коэффициентом близким к. Но тогда из (3.5.21) следует, что если частота квантования выбрана из условия, то в основной полосе частотможно приближенно принять, то есть частотные свойства непрерывной системы и ее дискретного эквивалента практически совпадают.

Рис. 3.14.

Заметим, что как следует из рис.3.14, на частотахэкстраполятор нулевого порядка может вносить существенные искажения. В частности, припроисходит полная потеря информации, так как коэффициент передачи экстраполятора на этих частотах обращается в ноль. Это явление потери информации на отдельных частотах известно как эффект поглощения частоты при квантовании[7].

Пример.В качестве примера рассмотрим непрерывную систему описываемую уравнением (3.3.18) (см. пример из раздела 3.3). Передаточная функция этой системы имеет вид

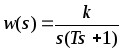, (3.5.24)

а -передаточная функция эквивалентной дискретной системы (при использовании экстраполятора нулевого порядка) определяется выражениями (3.3.20), (3.3.21).

Рассмотрим для простоты случай, когда запаздывание по управлению отсутствует . Тогда полагая в (3.3.21) , получим

,.

Применим для определенности следующие числовые параметры: ,,. Тогда-передаточная функция определится выражением

. (3.5.25)

Определим амплитудную и фазовую псевдочастотные характеристики данной дискретной системы. Для этого в (3.5.25) перейдем к -преобразованию с помощью подстановки. Будем иметь

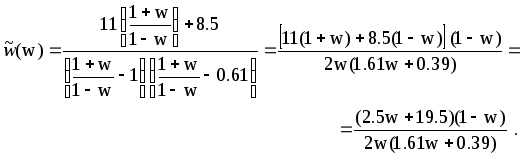
Для перехода к частотным характеристикам с использованием абсолютной псевдочастоты произведем замену . Тогда последнее выражение преобразуется к виду

. (3.5.26)

Обратим внимание, что статический коэффициент передачи точно, а постоянная времени инерционного звена приближенно совпадают с соответствующими параметрами исходной непрерывной системы, но по сравнению с (3.5.24) передаточная функция (3.5.26) имеет дополнительные две скобки в числителе.

Подставляя в (3.5.26) перейдем к псевдочастотной передаточной функции

,

которая в комплексной плоскости будет представлять годограф псевдочастотной АФЧХ. При этом искомые псевдочастотные АЧХ и ФЧХ будут иметь вид

.

Соответствующие логарифмические характеристики ипредставлены на рис.3.15. На этом же графике (пунктиром) изображены логарифмические характеристикиинепрерывной системы, построенные по передаточной функции (3.5.24) с учетом выбранных числовых параметров.

Из приведенных графиков, в частности, видно, что в области низких частот, где частотные характеристики исходной непрерывной системы и соответствующей ей дискретной системы близки, причем амплитудные логарифмические характеристики практически совпадают. Читателю предлагается самостоятельно построить и сравнить (в основной полосе частот) частотные характеристикииисходной непрерывной системы и характеристикиидискретной системы, определяемые по частотной передаточной функции.

Рис. 3.15.

85