2. 3.2. Передаточные функции (матрицы) дискретных систем

Понятие -передаточной функции (матрицы) дискретной системы.Передаточную функцию дискретной системы с одним входом и одним выходом можно определить как отношениеZ– илиD–изображения решетчатой функции выхода к соответствующему изображению решетчатой функции входа при нулевых начальных условиях. Следует заметить, что в силу более простой структурыZ–изображения (3.1.8), по сравнению сD–преобразованием (3.1.1), именно оно обычно используется для определения передаточных функций дискретных систем, которые в этом случае иногда называют-передаточными функциями.

Рассмотрим линейную многомерную дискретную систему с входами ивыходами. Используя понятие-передаточной функциимежду-ым выходом и-ым входом и применяя принцип суперпозиции, можно найтиZ-изображение любого выходапо изображениям входов, то есть

. ,. (3.2.1)

Если перейти к векторным переменным входов и выходов

; ,

то равенство (3.2.1) можно записать в векторно-матричной форме

, (3.2.2)

где - матрица размеров, состоящая из элементов, которую будем называть-передаточной матрицей многомерной дискретной системы.

Определение -передаточных матриц по разностным уравнениям.Рассмотрим многомерную дискретную систему, представленную разностными уравнениями в форме Коши

(3.2.3)

где ,,- векторы состояний, входов и выходов;,,- числовые матрицы соответствующих размеров.

Применим к уравнениям (3.2.3) Z–преобразование. Тогда используя свойство линейности изображений (3.1.11) и изображение смещенной (на один такт) решетчатой функции (3.1.13), получим

Выразим из первого уравнения

. (3.2.4)

Эту формулу можно рассматривать как способ решения разностного уравнения (3.2.3) с помощью Z–преобразования.

Используя (3.2.4), запишем выражение для при нулевых начальных условиях. Будем иметь

.

Сравнивая полученное выражение с формулой (3.2.2) заключаем, что -передаточная матрица дискретной системы (3.2.3) определится выражением

. (3.2.5)

При этом если система имеет один вход и один выход , то (3.2.5) превращается в скалярную передаточную функцию, представляемую отношением двух полиномов, то есть

, (3.2.6)

где - характеристический полином системы (3.2.3), а- некоторый полином, степень которого не превышает.

Пусть теперь дискретная система представлена разностными уравнениями в форме "вход-выход"

,, (3.2.7)

где и- числовые матрицы размеровисоответственно. Применим к уравнению (3.2.7)Z–преобразование при нулевых начальных условиях. Тогда используя (3.1.15) будем иметь

или представляя матричные полиномы в скобках с помощью полиномиальных матриц

,, (3.2.8)

получим уравнение (3.2.7) в Z–изображениях

. (3.2.9)

Заметим, что это уравнение можно получить из операторного представления (2.1.13) путем формальной замены оператора прямого сдвига на переменную.

Выражая из (3.2.9) изображение выхода и сравнивая полученное соотношение с (3.2.2), заключаем, что-передаточная матрица дискретной системы, представленной в форме "вход-выход", может быть определена по формуле

, (3.2.10)

которая, очевидно, совпадает с формулой для операторной передаточной матрицы (2.1.14) после замены на.

Заметим, что для односвязной системы полиномиальные матрицыи, определяемые соотношениями (3.2.8), превратятся в скалярные полиномыи, а (3.2.10) станет скалярной передаточной функцией вида (3.2.6).

Связь передаточной и весовой матриц дискретной системы.Рассмотрим решение разностного уравнения состояний, определяемое формулой (2.6.2), то есть

, (3.2.11)

где имеет смысл нормированной фундаментальной матрицы, которую можно рассматривать как матрицу, составленную из свободных реакций системы (3.2.3). Это, в частности, означает, что

, при. (3.2.12)

Применим к (3.2.11) Z–преобразование. Тогда используя свойство линейности и изображение свертки решетчатых функций (3.1.16), получим

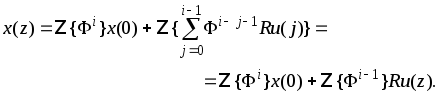
Учитывая теперь (3.2.12) и применяя свойство (3.1.14) будем иметь

.

Сравнивая полученное выражение с (3.2.4) нетрудно заключить, что

. (3.2.13)

Это выражение дает один из способов вычисления нормированной фундаментальной матрицы с помощью обратногоZ–преобразования, то есть

. (3.2.14)

Рассмотрим -передаточную матрицу (3.2.5), для которой с учетом (3.2.13) можно записать

Заметим, что, как было определено в разделе 2.6, представляет собой весовую матрицу дискретной системы. Таким образом, окончательно получаем

, (3.2.15)

то есть Z–изображение от весовой матрицы представляет собой передаточную матрицу. Это свойство, в частности, дает возможность нахождения весовой матрицы с помощью обратногоZ–преобразования.