1.6 Построение переходного процесса и определение прямых оценок качества системы

Исходная передаточная функция имеет вид:

Построим переходный процесс, для этого найдём уравнение переходного процесса методом обратного преобразования Лапласа.

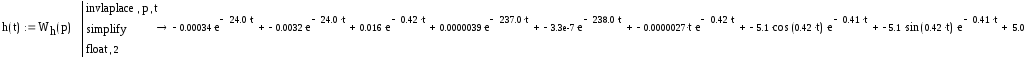
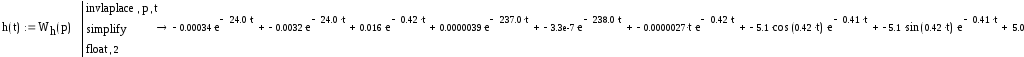
Определим прямые оценки качества, для этого построим график переходного процесса.

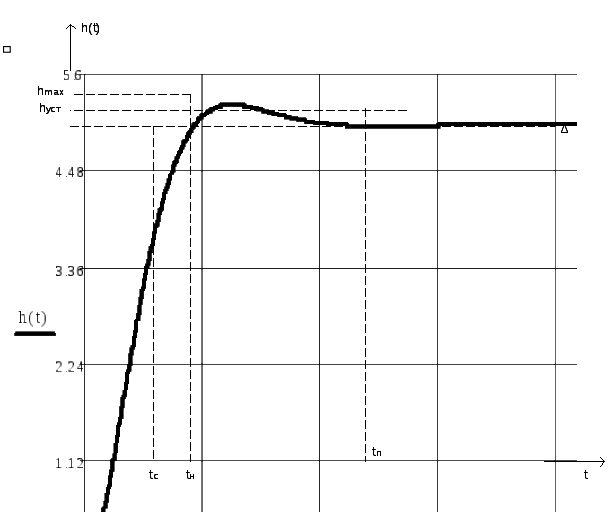
Рисунок 7 – График переходного процесса системы управления гидроприводом

Прямые оценки качества:

, тогда

-h_max=5.23

Время переходного процесса – это время, за которое регулируемая величина первый раз достигает у_уст t_пер=20,5

- перерегулирование определяется выражением. %

- колебательность – число колебаний системы от момента воздействия на неё до перехода в установившееся состояние. n=0

- время нарастания – время, при котором выходная величина достигает своего максимального значения. t_нар=7.5

- время первого согласования – время, за которое регулируемая величина первый раз входит в 5%-ю трубку. t_с=4.95

- период – время, за которое совершается полное колебание. T=0

1.7 Построение ачх и фчх, нахождение косвенных оценок качества сис-

темы управления гидроприводом

Для построения АЧХ воспользуемся формулой:

Построим график АЧХ.

Рисунок 8 – График АЧХ системы управления гидроприводом

Определим косвенные оценки качества системы.

-

- показатель колебательности

- резонансная частота – частота, при которой АЧХ достигает своего максимального значения.

- частота среза - частота, при которой АЧХ равно единице:

- полоса пропускания – это время наилучшего прохождения сигнала по системе, для её определения вычисляется величина:

Тогда W_пр=(0÷0.6)

Для построения ФЧХ воспользуемся формулой.

Построим график ФЧХ.

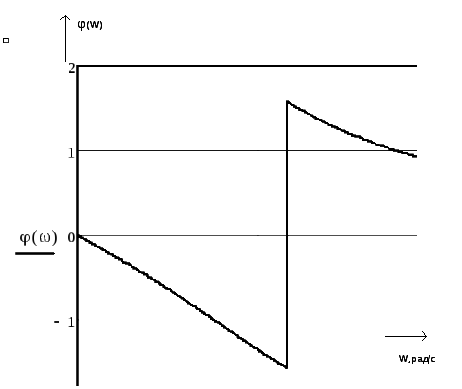
Рисунок 9 – График ФЧХ системы управления гидроприводом

Вывод: в ходе исследования линейной системы уравнения гидропривода преобразована структурная схема САУ, получена общая передаточная функция системы. Проведён анализ устойчивости данной системы по критерию Гурвица, построены графики переходного процесса и амплитудно – частотной характеристике и найдены прямые и косвенные оценки качества системы.

По построенным амплитудно – частотной характеристике и переходному процессу можно судить о прямых и косвенных оценках качества системы: быстродействие системы составляет t_п=20.5 с, а полоса пропускания сигнала находится в промежутке (0; 0.6).

2 ИССЛЕДОВАНИЕ НЕЛИНЕЙНОЙ САУ

2.1 Техническое задание. Исследование устойчивости нелинейных

систем автоматического управления.

Структурная схема нелинейной системы управления представлена на рисунке 10. Для построения фазового портрета структурную схему преобразуем так, чтобы нелинейный элемент и линейная часть были соединены последовательно.

Рисунок 10 – Структурная схема нелинейной системы управления гидроприводом

Передаточные функции нелинейной системы управления имеют следующий вид:

W₁=24/(2.4p+1),

W₃=0.42,

W₄=24/(2.4p+1)

W₅=0.42/(0.042p+)(0.0042p+1)

W₆=0.1/(0.01p+1).

НЭ – нелинейный элемент (идеальное реле)

Нелинейный элемент имеет характеристику следующего вида:

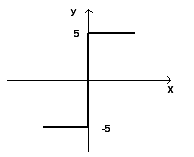
Рисунок 11 – График, описывающий нелинейный элемент

5, если у(t)>0

-5, если y(t)<0

F(y(t))=

2.2 Упрощение структурной схемы нелинейной САУ гидроприводом

Разомкнём систему перед линейным элементом

Рисунок 12 – Структурная схема нелинейной САУ

Найдём передаточную функцию линейной части

Получим замкнутую систему:

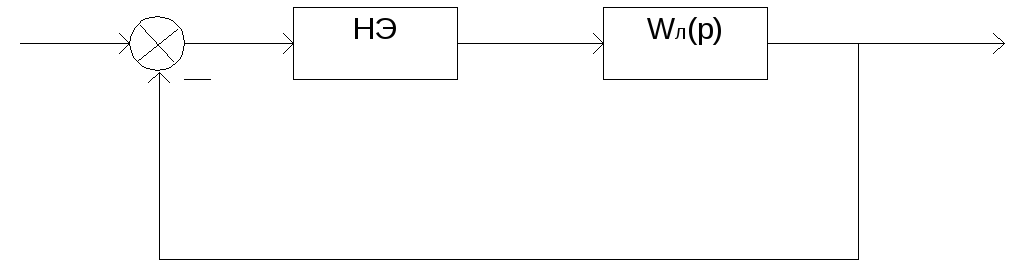
Рисунок 13 – Замкнутая нелинейная система управления гидроприводом

2.3 Построение фазового портрета системы управления гидроприводом

Для построения фазового портрета необходимо исследовать передаточную функцию линейной части системы.

Так как фазовый портрет строится для систем второго порядка, то передаточная функция линейной части будет иметь вид.

Передаточная функция W(p)=x/x₁ ,значит

Приводим уравнение к виду:

(6p²+4.9p+1)x=10x₁

Подставим значение для x₁ из условия для нелинейной часть, получим:

6p²x+4.9px+1x=50

6p²x+4.9px+1x=0

6p²x+4.9px+1x=-50

Преобразуем систему, получим:

6p²x+4.9px+1x-50=0

6p²x+4.9px+1x=0

6p²x+4.9px+1x+50=0

Введём замену pⁱx=y_i и разделим все члены уравнения на 6.

y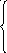₂=-0.816y₁-0.166y₀+50

y₂=-0.816y₁-0.166y₀

y₂=-0.816y₁-0.166y₀-50

Создадим матрицу для решения дифференциального уравнения:

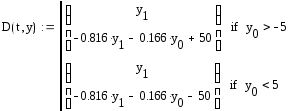
В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицу начальных условий:

Принимаем количество точек, равное 1000 и конечное время интегрирования 100.

По введённым данным получим фазовый портрет.

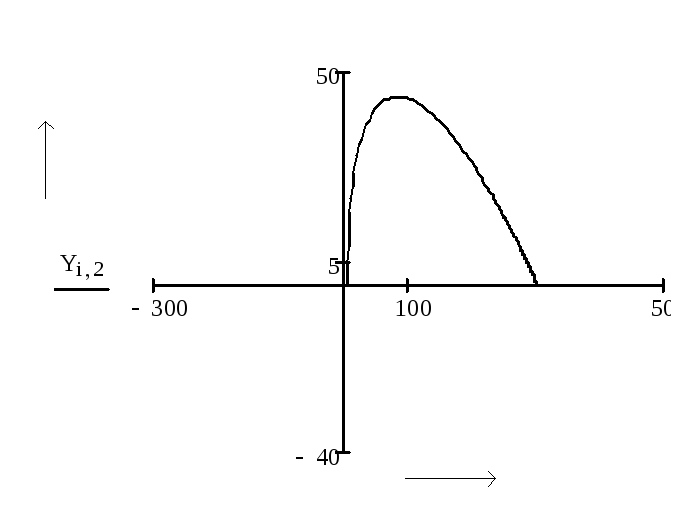
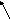
Рисунок 14 – Фазовый портрет нелинейной системы управления

Вывод: в результате построения фазового портрета нелинейной системы управления гидроприводом видно, что фазовая траектория закручивается к началу координат, что соответствует затухающему колебательному процессу. При движении к состоянию устойчивости амплитуда колебаний постоянно уменьшается. Получаем, что амплитуда колебаний примет нулевое значение, то есть нелинейная система со звеном идеальное реле устойчива.