3. Барометрическая формула

Атмосфера, то есть воздушная оболочка Земли, обязана своим существованиям наличию теплового движения молекул и силы притяжения их к Земле. При этом в атмосфере устанавливается вполне определенное распределение молекул по высоте. Соответственно этому, устанавливается определенный закон изменения давления воздуха с высотой, который нетрудно найти.

Возьмем вертикальный столб воздуха. Считаем, что при х=0, y поверхности Земли р=р₀ , а на высоте х давление равно р. При увеличении высоты на dx давление уменьшается на dp. Известно, что давление воздуха на некоторой высоте равно весу вертикального столба воздуха с площадью равной единице, находящегося над этой высотой. Поэтому, dp равно разности весов столбов воздуха с площадью s=1 м²на высотах x и x+dx, то есть, равно весу столба воздуха высотой dx с площадью основания 1 м²:

p-dp-p= -dp= ρgdx 1 м², значит, dp= -ρgdx, плотность ρ= m₀N/V= m₀n, (m₀N = m – масса всех молекул).

Из молекулярной физики известно, p= nkT => n= p/kT => ρ= m₀ p/kT

и тогда, подставляя значение плотности, получим: dp= (-m₀g/kT)pdx. После разделения переменных: dp/p= (-m₀g/kT)dx

Считая для простоты температуру постоянной на всех высотах (что не так) после интегрирования найдем:

lnp= (-m₀g/kT)x +lnC , откуда: p= Ce^(-^m₀^g^/^kT⁾^x . Постоянную C находим из начальных

условий: при х= 0 р= р₀, то есть р₀=C и тогда:

р= р₀e^(-^m₀^g^/^kT⁾^x

или с учетом m₀= M/N_A:р= р₀e^(-^Mg^/^R^T⁾^x - барометрическая формула, т.е., давление с высотой убывает по экспоненциальному закону.

Для градуировки барометров необходимо внести поправки на Т. Так как, давление пропорционально концентрации молекул в единице объема, то: n= n₀ e^(-^mg^/^k^T⁾^x - закон убывания концентрации молекул, а значит, плотности с высотой.

Видно, что атмосфера Земли в принципе, простирается до ∞. На больших высотах необходимо учесть, что g – меняется с высотой: g(r)= γM/(r+x)².

Б-18

1.Связь между потенциальной энергией и силой для консервативного поля.

2.Постулаты Эйнштейна.

Распределение Больцмана.

1. Связь между потенциальной энергией и силой для консервативного поля.

Взаимодействие частицы с окружающими телами можно описать либо с помощью сил либо с помощью потенциальной энергией. Первый способ более общий , т.к. он применим и к силам, для которых нельзя ввести понятие потенциальной энергии (силы трения). Второй способ удобен тем, что существует связь между потенциальной энергией и силой со стороны поля. Зная эту связь, можно по виду зависимости — функции положения частицы в поле, находить поле сил .

Найдем эту связь. Известно, что работа консервативных сил при перемещении частицы из одной точки статического поля в другую может быть представлена в виде убыли потенциальной энергии частицы 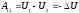. Это можно записать и для элементарного перемещения .

т.к. ; — элементарный путь или ; — убыль потенциальной энергии в направлении перемещения ; отсюда: т.е. проекция силы поля в данной точке на направление перемещения 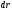равна убыли потенциальной энергии в этом направлении. Символ указывает, что произведение берется по определенному направлению. Перемещение можно брать в любом направлении, например вдоль осей . Если вдоль то ; а , — проекция силы на орт (а не на перемещение , как в случае 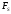). Т.о. относительно оси можно записать . Символ означает, что при дифференцировании должна расти как функция одного аргумента , а остальные аргументы — . Значит ; . Зная проекции можно найти и сам вектор или . Скобка называется градиент скалярной функции , и обозначается или т.о. 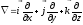— символический вектор или оператор Гамильтона. — формально можно рассматривать как произведение символического вектора на скаляр т.е. сила действующая со стороны поля на частицу равна со знаком минус градиент потенциальной энергии частицы в данной тоске поля. Т.о. зная 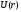можно найти .