1. Энергия и робота

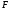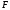Пусть частица под действием силы совершает перемещение по некоторой траектории 1-2. в общем случае сила может меняться во времени по модулю, например, но не элементарном перемещении 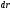её можно считать .

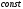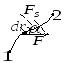
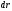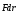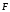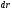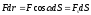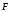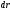
Действие силы на перемещении характеризуется физической величиной, равной скалярному произведению , которое называется элементарной работой силы на перемещении . Её можно ещё записать как , где — угол между и 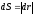- элементарный путь 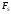проекция вектора 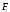на вектор

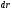
Значит элементарная работа (*)

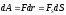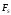
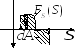
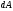- величина алг. она 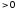и и 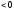и = 0 при .

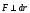Суммируя ( интегрируя ) по всем элементарным участкам пути от 1 к 2 найдем работу силы 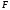на данном пути.

.

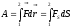Геометрический смысл этого выражения виден из рисунка 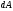— полоска; 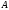— площадь под прямой. Над осью работа положительна, под — отрицательна.

.

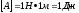Найдем для примера работу некоторых центральных сил.

4. Работа гравитационной или кулоновской силы вида 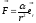; 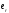—орт радиус вектора 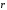. Элементарная работа не ???? 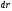: 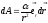; 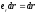— приращение модуля вектора ; .

   

   

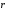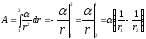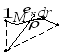
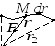
5. Работа упругой силы 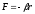; — радиус вектор частицы М относительно точки О. элементарная работа ; .

   

   

   

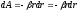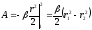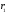
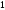
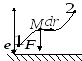
6. Работа сил тяжести. 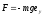; ; 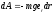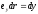— приращение координаты . ; .

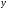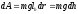
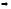
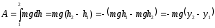
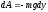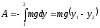Работа всех этих сил не зависит от формы пути а только от положения точек 1,2. Эта особенность не всех сил. Силы трения не обладают таким свойством.

3. Средняя арифметическая скорость <v> по определению равна отношению суммы скоростей всех молекул единицы объема к числу молекул единицы объема.

Число молекул в единице объема dn_v, скорости которых заключены в интервале от v до v+dv равно nf(v)dv; Сумма скоростей всех таких молекул равна vnf(v)dv. Чтобы найти сумму скоростей всех молекул, обладающих любыми скоростями, нужно это выражение проинтегрировать по всем возможным значениям скорости от 0 до ∞. Следовательно, сумма всех скоростей молекул ∫vnf(v)dv, а <v> = 1/n∫ vnf(v)dv , т.е.,

∞

0

∞

0

∞

0

<v> = ∫vf(v)dv , подставив f(v), получим:

∞

0

<v> = 4/√π (m/2kT)^3/2∫ v³e dv = 4/√π (m/2kT)^3/2∫ v²e vdv

vdv = d(v²)/2, значит <v> = 4/√π (m/2kT)^3/2½∫ v²e d(v²)

Введем новую переменную Z=mv²/2kT : ½∫ v²e d(v²) = ½ (2kT/m)²∫Ze^-ZdZ, тогда, учитывая, что ∫Ze^-ZdZ =1, получим:

<v> = 4/√π (m/2kT)^3/22(kT/m)² = √8kT/πm

Б-14

1. Мощность.

2. Волновое уравнение.

3. Число ударов молекул о стенку и давление газа на стенку.

1. Мощность по определению это работа, выполненная за единицу времени. Если за промежуток времени 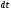сила 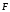совершает работу 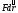, то мощность, развиваемая этой силой в данный момент времени 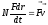т.е. скалярное произведение 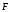и .

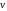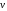— скорость движения точки приложения силы.

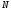— как и работа величина алгебраическая.

Зная 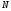можно найти работу, которая совершает сила 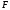за время

.

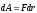
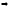
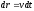
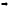
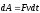
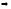
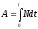
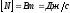3. Число ударов молекул о стенку

Рассмотрим находящийся в равновесии газ, заключенный в некотором сосуде. Допустим, что молекулы газа движутся только вдоль трех взаимно ┴ направлений. Это можно допустить из-за хаотичности движения молекул. Если в сосуде находится N молекул, то в любой момент времени вдоль каждого из направлений будет двигаться N/3 молекул и половина из них - N/6 вдоль данного направления в одну сторону, а вторая половина - в другую. Следовательно, в интересующем нас направлении по нормали к данному элементу ΔS стенки сосуда движется N/6 молекул, а для единицы объема - 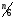, n – концентрация молекул.

Пусть все молекулы движутся с одинаковой средней скоростью <v>. За время Δt элемента стенки ΔS достигают все молекулы, находящиеся в параллелипипеде с площадью основания ΔS и длиной 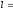<v>Δt. Их число Δν = (n/6)ΔS<v>Δt, следовательно, число ударов о единичную площадку в единицу времени

Δν/ΔSΔt = (n/6)<v>.

Если отказаться от допущения, что все молекулы движутся с одинаковой скоростью v = <v>, то необходимо выделить в единице объема молекулы, скорости которых лежат в интервале от v до v+dv. Их число -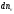. Количество ударов таких молекул, долетающих до площадки ΔS за время Δt равно dν_v = (1/6)(dn_vΔSvΔt). Полное число ударов:

v_max

0

v_max

0

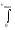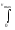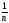
Δν = dν_v = 1/6ΔSΔt vdn_v = Выражение 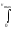vdn_v по определению является средней скоростью молекулы, тогда Δν = 1/6ΔSΔtn<v> , т.е., получили то же самое значение числа ударов.

Давление газа на стенку сосуда

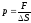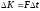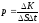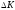Давление по определению можно записать: , а поскольку, из второго закона Ньютона: , то . Значит, необходимо вычислить импульс , передаваемый всеми молекулами со всеми скоростями единице площади за единицу времени.

Число молекул со скоростью v из общего количества n, долетающих до площадки ΔS за время Δt равно:

dν_v = (1/6)(dn_vΔSvΔt)

Далее, умножив это число на импульс, сообщаемый каждой молекулой при ударе равный – 2mv, получим импульс, сообщаемый площадке ΔS за время Δt этими молекулами. Изменение импульса одной молекулы равно K₂-K₁= -2mv, значит, импульс передаваемый молекулой стенке равен +2mv. Импульс, передаваемый молекулами со скоростями, лежащими в интервале от v до v +dv

v_max

0

v_max

0

равен 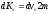v.

Импульс, передаваемый всеми молекулами со всеми скоростями:

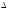K = 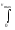(1/6)(dn_vΔSvΔt)2mv = 1/3 m ΔSΔt 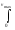v²dn_v (*)

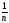
Выражение 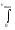v²dn_v представляет собой среднее значение квадрата скорости молекул, тогда, заменив в (*) интеграл и, разделив это выражение на ΔS и Δt, получим давление газа на стенку сосуда:

р = 1/3mn<v²>

т.к. m<v²>/2 = <ε_пост> по определению, получим:

р =2/3n<ε_пост>

- основное уравнение молекулярно- кинетической теории. Это уравнение раскрывает физический смысл макропараметра р: давление определяется средним значением кинетической энергии поступательного движения молекул.

Б-15

1. Консервативные силы.

2. Энергия волны. Объемная плотность энергии волны.

3. Средняя энергия молекул с учетом вращательных и колебательных степеней свободы.

1. Консервативные силы

Если в каждой точке пространства на частицу, помещенную туда, действует сила, говорят, что частица находится в поле сил, например в поле сил тяжести, гравитационной, кулоновской и т.д. Поле сил может быть постоянным во времени, тогда оно называется стационарным. Стационарное поле в одной системе отсчета м.б. в другой. В стационарном поле сила, действующая на частицу, зависит только от её положения в пространстве.

Работа, которую совершает сила поля по перемещению частиц из т.1 в т.2 зависит, в общем случае от формы пути между этими точками, например при действии 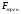. Однако, имеются стационарные силовые поля, в которых работа над частицей силами поля не зависит от пути между т.1 и т.2. Силы обладающими такими свойствами называются консервативными. Это свойство можно сформулировать другим способом: силы поля являются консервативными, если работа в стационарном полена любом замкнутом пути равна =0.

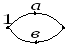
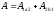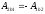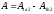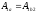поскольку то . А т.к. работа не зависит от пути , то .

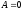К неконсервативным силам относятся силы трения и сопротивления. Работа этих сил зависит от пути между начальным и конечным положением частицы и не равна 0 на замкнутом пути.

3. Средняя энергия молекул

Из уравнения состояния идеального газа p=nkT и выражения для давления газа на стенку сосуда р =2/3n<ε_пост> следует, что

<ε_пост> = 3/2kT (1), откуда можно заключить, что температура есть величина, прямо пропорциональная средней энергии поступательного движения молекул.

Поступательно движутся молекулы газа. Молекулы твердых и жидких тел совершают колебания вблизи положений равновесия.

Из выражения (1) видно, что <ε_пост> зависит только от Т и не зависит от массы молекулы.

Т.к., <ε_пост> = <mv²/2> = m<v²>/2, то из сравнения с выражением (1), получим: <v²> = 3kT/m а средняя квадратичная скорость:

v_ср.кв. = √<v²> = √3kT/m .

Можно представить <v²> = <v²_x>+<v²_y>+<v²_z> = 3<v²_x>, поскольку, все направления движения молекул равноправны, т.е., <v²_x> = <v²_y> = <v²_z>, тогда:

<v²_x> = 1/3<v²> = kT/m

Формула (1) определяет энергию поступательного движения молекул. Наряду с этим движением возможны также вращение молекул и колебания атомов, входящих в состав молекул. Например, для двухатомной жесткой молекулы это вращение вокруг двух взаимно перпендикулярных осей, проходящих через центр масс молекулы. Эти виды движения также связаны с запасом энергии молекулы. Ее полную энергию позволяет определить, устанавливаемое статистической физикой, положение о равнораспределении энергии по степеням свободы молекулы. Такую гипотезу впервые высказал Больцман.

Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано ее положение. Положение материальной точки определяется в пространстве значением трех координат, она имеет три степени свободы. Одноатомной молекуле следует приписывать три степени свободы, двухатомной: в зависимости от характера связи между атомами – либо три поступательных и две вращательных (жесткая связь), т.е. всего пять степеней; либо n = 3+2+1=6 с учетом колебательной степени свободы для нежесткой молекулы.

Поскольку ни одна из поступательных степеней свободы не имеет преимущества перед остальными, на каждую из них приходится в среднем одинаковая энергия 1/2kT. Согласно закону равнораспределения на каждую степень свободы молекулы приходится в среднем одинаковая энергия, равная 1/2kT. Согласно закону среднее значение энергии одной молекулы <ε> будет тем больше, (при одинаковой Т), чем сложнее молекула и чем больше у нее степеней свободы. При определении <ε> необходимо учесть, что колебательная степень свободы обладает вдвое большей «энергетической емкостью» по сравнению с поступательной или вращательной. Это объясняется тем, что колебательное движение связано с наличием кинетической и потенциальной энергии, поэтому на колебательную степень приходится (1/2kT+1/2kT) = kT, т.е., одна половинка в виде ε_кин , а вторая - ε_пост.

Т.о. средняя энергия молекулы: <ε> = (i/2)(kT),

Где i- сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы молекул.

i = n_пост+n_вращ+2n_кол , здесь n – число степеней свободы.

Для молекул с жесткой связью i совпадает с числом степеней свободы.

Б-16

1. Центральные силы.

2. Пространство и время в ньютоновской механике.

3. Внутренняя энергия и теплоемкость C_v и C_p идеального газа.

1. . Центральные силы.

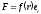
Всякое силовое поле вызвано действием определенных тел. Сила, действующая на частицу в этом поле обусловлена взаимодействием этой частицы с телами. Силы, которые зависят только от расстояния между взаимодействующими частицами и направлены вдоль прямой их соединяющей называются центральными (гравитационные, кулоновские, упругие). Центральные силы можно записать как 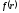зависит только о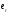т , — орт 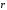частицы 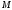относительно О. докажем что центральная сила является консервативной. Для частицы 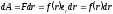; 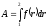. 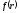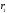Этот интеграл не зависит от формы пути, а зависит только от вида функции и от и 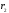т.е. от пределов интегрирования. Если на частицу действует несколько центральных сил, то работа 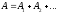, а т.к. работа каждой из них не зависит от пути, то и 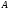не зависит.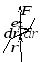

3. Внутренняя энергия и теплоемкость идеальных газов

В идеальном газе молекулы не взаимодействуют между собой, внутренняя энергия одного моля газа:

U_м = N_A<ε> = i/2 N_AkT = i/2 RT . U_м = i/2RT.

Если вспомнить, что по определению: C_v = δQ/dT = dU/dT, поскольку, δQ = dU+pdV, а для изохорного процесса dV = 0.

Тогда C_v = (i/2) R , а, учитывая, что C_р = C_v+R, получим:

C_р = (i+2)/2 R

Следовательно, коэффициент Пуассона γ = C_p/C_v = (i+2)/i , таким образом, γ определяется числом и характером степеней свободы молекулы.

Согласно этой ф-лы для одноатомной молекулы i = 3 и γ = 1,67; жесткой двухатомной i =5 и γ = 1,4; упругой двухатомной i = 7, а γ = 1,29. В области температур, близких к комнатной, это хорошо согласуется с опытом. Однако, в широком температурном интервале это не так. Оказывается, что вращательная и колебательная энергии молекулы квантованы. При низких Т вращательные и колебательные степени свободы не возбуждены. Молекула Н₂ , например, ведет себя как одноатомная в этой области температур, i = 3. В области Т ≈ 500К вращательные степени «разморожены» <ε> > ε_вращ и молекула Н₂ ведет себя как жесткая двухатомная с = 3+2 = 5. При Т>1000К энергии <ε> достаточно для возбуждения колебательной степени свободы, «включены» все степени свободы, i = 7.

Б-17

1. Потенциальная энергия частицы в поле.

2. Опыт Майкельсона и Морли.

3. Барометрическая формула.

1. Потенциальная энергия частицы в силовом поле.

То обстоятельство, что работа консервативной силы (для стационарного поля) зависит только от начального и конечного положений частицы в поле, позволяет ввести важное физическое понятие потенциальной энергии (функции состояния). Возьмем стационарное поле консервативных сил, например электростатическое поле в котором мы перемещаем частицу (заряд) из разных точек 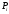в некоторой фиксированной точке О (точка отсчета). Найдем работу сил поля. Поскольку работа сил поля не зависит от пути, то остаётся зависимость её только от положения т.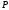 (О— фиксировано) т.е. от предела интегрирования

(*).

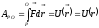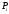
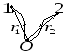
Это значит, что данная работа будет некоторой функцией радиус-вектора 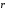точки 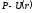. Функцию 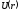называют потенциальной энергией частицы в поле сил. Теперь найдем работу при перемещении частицы из т.1 в т.2. Т.к. она не зависит от формы пути: то 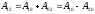или с учетом (*)

;

;

(**)

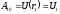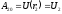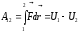Правая часть представляет убыль потенциальной энергии, т.е. разность начальную и конечную значений потенциальной энергии. ( 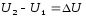— приращение); (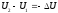— убыль). Т.о. работа сил Оля на пути 1—2 равна убыли потенциальной энергии. Так как работа сил поля определяется лишь разностью энергий в двух точек, а не их абсолютного значения, то частица в т.О можно приписать любое, наперед выбранное значение потенциальной энергии.

Однако, как только зафиксирована потенциальная энергия в одной, какой-либо точке, значения её во всех остальных точках поля определяется однозначно выражением (**). Эта формула позволяет найти вид 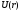для любого стационарного поля консервативных сил. Для этого достаточно вычислить работу совершаемую силами поля между двумя любыми точками и представить её в виде убыли некоторой функции 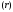, которая и есть потенциальной энергией. Так и было ране сделано при вычислении работы гравитационной, упругой и силы тяжести. Отсюда видно, что потенциальная энергия частицы в данных полях имеет вид

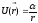— гравитационная, кулоновская +С – постоянная.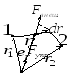

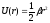— упругой +С

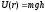— в поле тяжести.

Отметим еще раз, что потенциальная энергия определяется с точностью до некоторой постоянной величины, что несущественно, т.к. во всех формулах входит разность её значения в двух положениях частицы, поэтому постоянная выпадает, и её опускают. Кроме этого важно заметить, что потенциальную энергию следует относить не к частице в поле а к системе взаимодействующих частиц и тела, создающего поле. При данном характере взаимодействия потенциальная энергия зависит только от положения частицы относительно этого тела.