4.3. Геометрический анализ голограмм

Для того чтобы понять свойства образующихся при восстановлении мнимого и действительного изображений, в том числе увеличение и геометрические искажения, достаточно проанализировать голограммы точечного источника. Последних в природе не существует, однако протяженные источники и освещенные объекты можно рассматривать как набор точечных источников.

Рассмотрим один предметный точечный источник. Опорный источник так же считаем точечным. Далее делаем следующие предположения:

1. освещающие волны полностью когерентны;

2. голограмма экспонируется и проявляется таким образом, чтобы ее амплитудное пропускание было пропорционально интенсивности интерференционной картины (линейная запись);

3. голограммы действуют как плоские (двумерные) дифракционные решетки.

Считаем, что амплитуда сферической волны, исходящей из каждого точечного источника, приблизительно постоянна в плоскости голограммы.

Рассмотрим, каким образом предметная, опорная и освещающая волны в любой точке Q в плоскости голограммы характеризуются фазой в этой точке по отношению к фазе в фиксированном начале координат O (рис. 4.4). Считая голограмму очень тонкой, относительные фазы можно рассчитать по геометрическим разностям хода световых лучей.

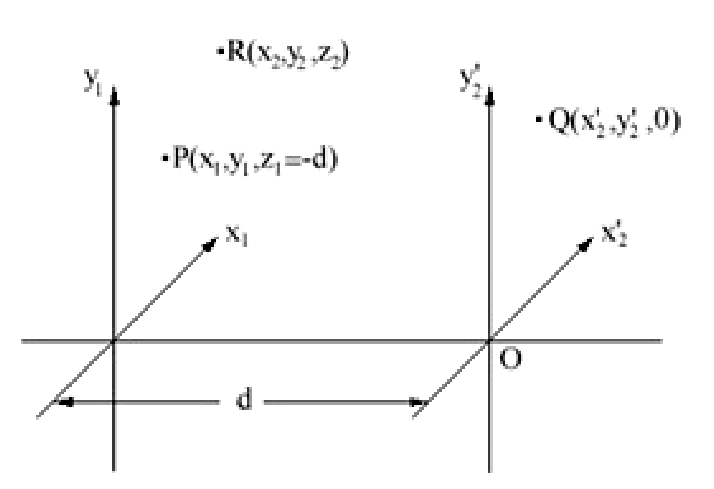
Рис. 4.4. Геометрия схемы записи голограммы

Пусть – комплексная амплитуда волны, приходящей в плоскость голограммы из точечного предметного источника, rr₀exp (i₂) – то же для опорной волны. Тогда регистрируемая в плоскости голограммы интенсивность

, (4.13)

причем наибольший интерес представляют интерференционные члены с разностью фаз (_r  _a). Предметный источник расположен в плоскости x₁ y₁, отстоящей от начала координат на r₁ = –d. Начало координат в плоскости (штрихи пока не обсуждаем до рассмотрения увеличения голограммы). Опорный точечный источник R расположен в некоторой произвольной плоскости x_r y_r на расстоянии z_r от плоскости голограммы. Поскольку P и R – точечные источники, излучающие сферическую волну, фаза ее в любой точке пространства пропорциональна радиальному расстоянию от этой точки до источника. Разность фаз _a, соответствующая разности хода PQ–PO, равна

.

Знак здесь выбирается так: если волна расходящаяся и если PQ > PO, то Так же и для опорной: «+» для сходящейся, «–» для расходящейся. Тогда

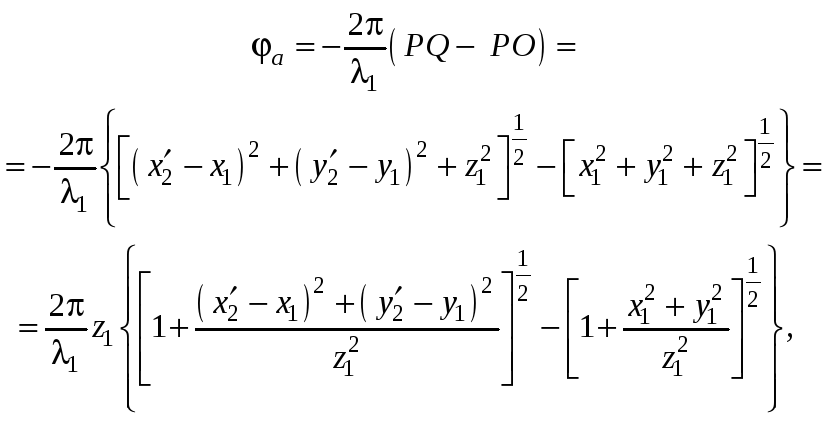(4.14)

при этом предполагается, что Z₁ отрицательно, поэтому знак _а остается отрицательным. Если P и Q не удалены от оси z и z₁ достаточно велико, то _а в первом приближении (достаточно точно) представляется в виде

. (4.15)

Фаза опорной волны в точке Q рассчитана аналогично:

. (4.16)

Разность фаз опорной и предметной волн:

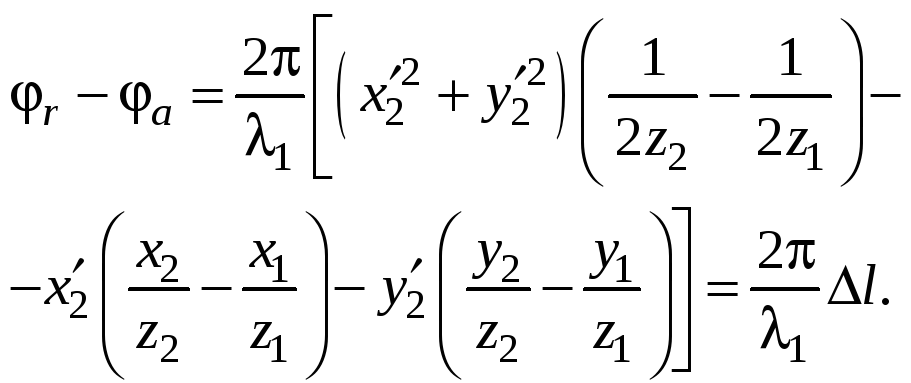(4.17)

Величина в квадратных скобках – разность хода волн в точке Q. Не останавливаясь далее на получении голограммы, перейдем сразу к ее восстановлению.

Предположим, что полученную голограмму можно до восстановления увеличить или уменьшить. Это учитывается обозначением координат в плоскости голограммы через , , где m – линейное увеличение. Кроме того, длина волны ₂ при восстановлении не обязательно должна быть равна длине волны ₁ при получении. Их отношение обозначим  = ₂/_1.

Восстанавливающая волна исходит из точечного источника С (x_cy_cz_c). Последний не обязательно совпадает с исходным опорным источником. Дифракция происходит за счет двух членов комплексного пропускания, т. е. , где первый член дает действительное изображение, а второй – мнимое. Фаза дифрагированной волны:

обозначается как _R = _c+_r–_a. Ааналогично _V = _c–_r+_a. Как и выше для _a и _r , запишем в первом приближении _с:

. (4.18)

Подставляя _c,_r и _a, получаем

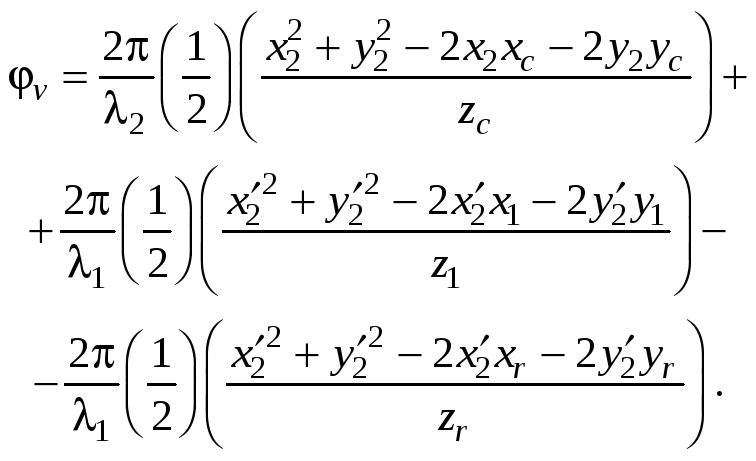_(4.19)

Вводя , и  = ₂/₁, запишем

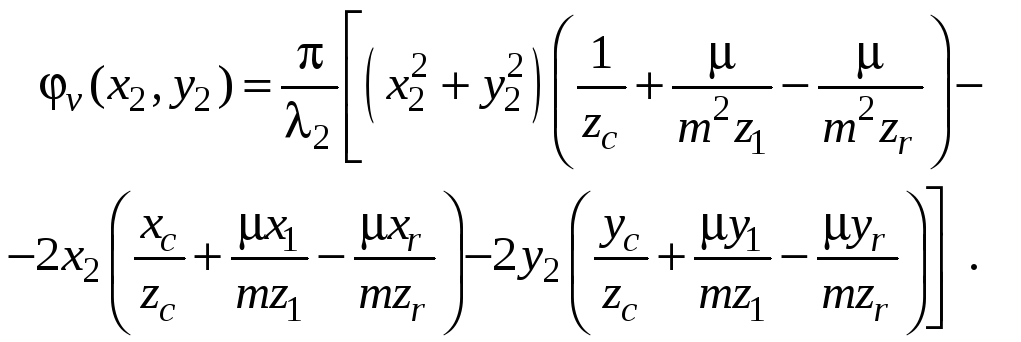(4.20)

Аналогично

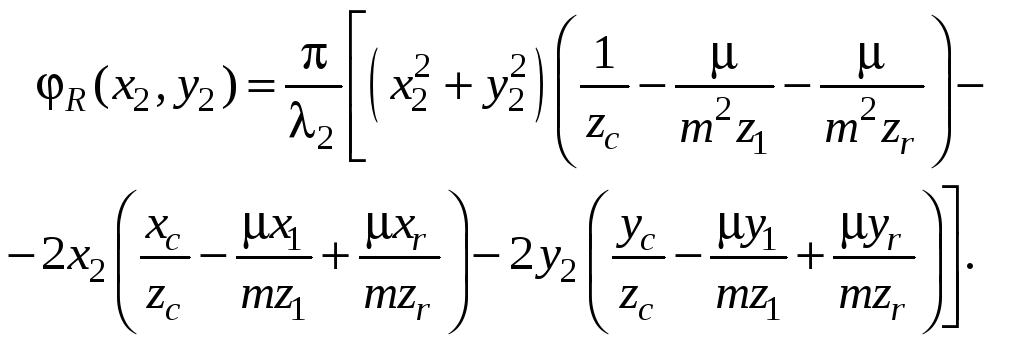(4.21)

Опять же в первом приближении распределение фазы сферической волны в плоскости голограммы:

. (4.22)

Здесь z₃ – расстояние от голограммы до плоскости изображения, а x₃ и y₃ – координаты изображения точки P в плоскости изображения. К такому виду и надо привести _v и _R, тогда в первом приближении восстановленные волны будут сферическими, сходящимися или расходящимися в зависимости от знака _V и _R.

Очевидно, что к желанной форме мы приходим, если вынесем за скобки коэффициент при (x₂²+y₂²) в выражениях для _V и _R. Таким образом, восстановленное изображение представляет собой точечный источник с координатами (x_3V, y_3V, z_3V) для _V и (x_3R, y_3R, z_3R) для _R, где

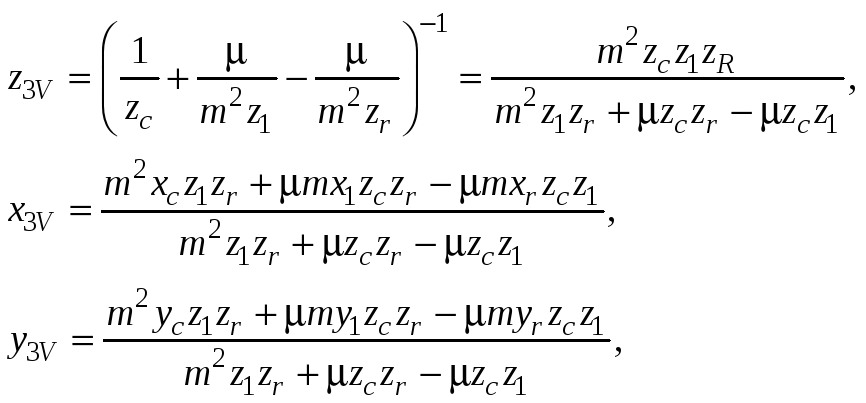(4.23)

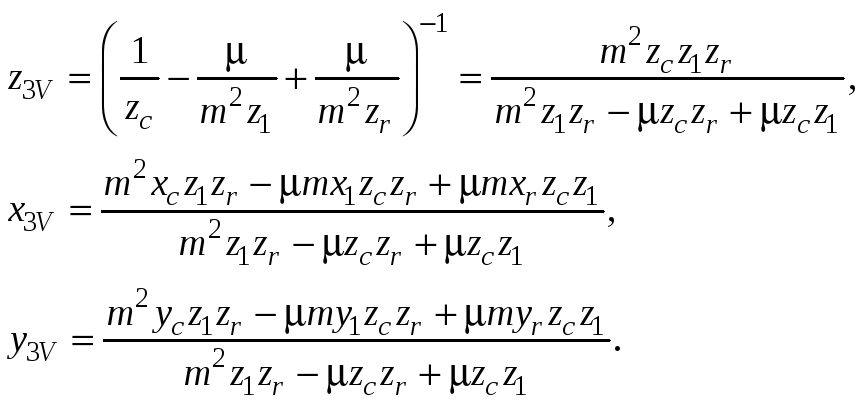(4.24)

Вместе с соотношениями, определяющими положение восстановленного изображения, найдем выражение для поперечного увеличения M_non: . Из вышеприведенных выражений имеем

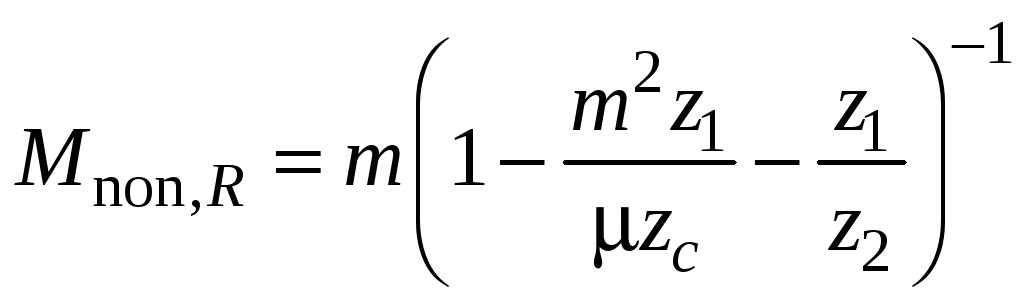, (4.25)

. (4.26)

Для углового увеличения

(4.27)

получаем .

Теперь рассмотрим свойства изображений для основных типов голограмм.

1. Начнем с осевых голограмм, когда опорный, предметный и освещающий источники лежат на одной оси, так, что x_r = x₁ = x_c = 0. Рассматриваем только x- и z-координаты изображения (y-координата не имеет дополнительной информации). Примем также   m = 1 и z_c = z_r, что соответствует условию опыта Габора. Тогда

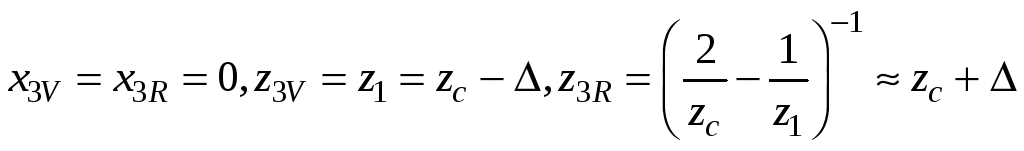. (4.28)

Здесь  = z_r – z₁ – некая величина (отрицательная), причем /z₁ << 1. То есть изображения расположены симметрично относительно освещающего источника на небольшом расстоянии от него. А так как z_c отрицательно, оба изображения мнимые. Поперечное же увеличение (для   m = 1) имеет вид

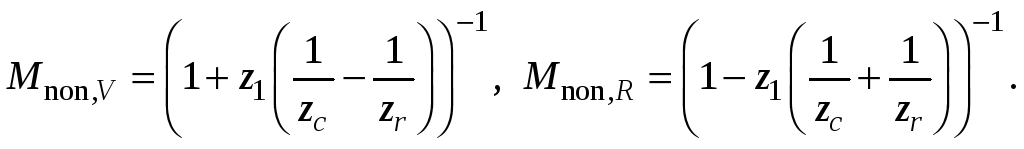(4.29)

Если освещающий источник расположен в той же точке, где находится исходный опорный, т. е. z_c = z_r, то M_{non, V} = 1 и M_{non, R}  –1 (так как z₁/z_r  1). Последнее говорит о перевернутом изображении.

Угловое же увеличение M_угл =  / m = 1. Наконец можно показать, что продольное увеличение M_пр = (₁/₂) M_non. Если же расположить объект вблизи голограммы (|z₁| << |z_r|), то для x_r = x₁ = x_c = 0, и   m = 1, z_c = z_r имеем

. (4.30)

И при использовании плоской опорной волны (z₂) z_3V = z₁, и z_3R = –z₁, т. е. действительное и мнимое изображения симметричны относительно голограммы, причем оба они прямые, так как M_non,V  =  M_non,R  = +1. Вообще говоря, если масштаб голограммы неизменен (m = 1), то поперечное увеличение для голограммы, освещаемой плоской волной (z_c = 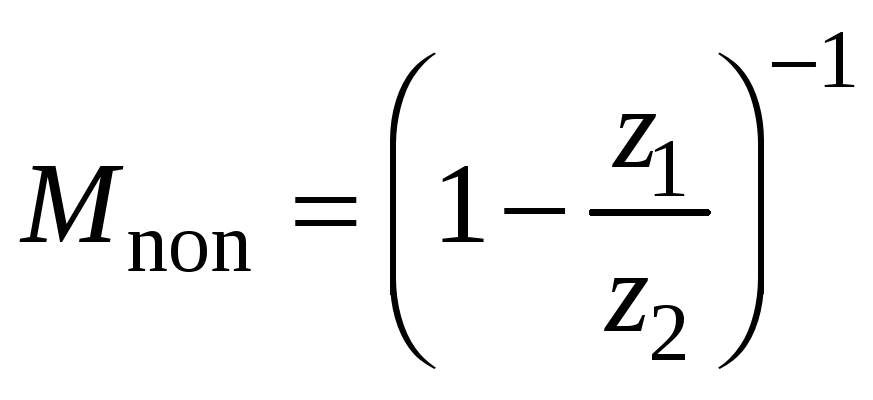), зависит только от соотношения z₁/z₂, но не зависит от длины волны. Если же и опорная волна была плоской (z₂  ), то при восстановлении всегда отсутствует увеличение.

2. Схема Лейта и Упатниекса с внеосевым опорным пучком. Вновь считаем размеры голограммы неизменяемыми (m = 1), а волны, освещающую и опорную, – плоскими (z_c = z_r = ). При этих условиях

(4.31)

где _c  tg_c = x_c/z_c и _r  tg_r =  x_r/z_r – углы освещающего и опорного пучков с положительным направлением оси z.

Если освещающая волна идентична опорной (   и _с = _r), то x_3V = x₁, z_3V = z₁, x_3R = x₁ – 2z₁_r, z_3r =  – z₁, т. е. мнимое изображение появится в месте исходного объекта, а действительное – в плоскости на расстоянии z₁ по другую сторону от освещающего источника. Оба изображения прямые.

Часто бывает полезно определить угол дифракции при освещении голограммы плоской волной. Полагая _с = _r = 0, найдем углы дифракции для волны с фазой _V и _R

, . (4.32)

В общем случае, когда плоская опорная и освещающая волны идут под углом к оси, для углов дифракции имеем

_3V = ₁ + _с – _r, _3R = – ₁ + _с + _r.

Если взять ₁ = –, _r = + , _с = +,  = 1, то _3V =  – , _3R = +3.

3. Все источники находятся на одинаковом расстоянии от голограммы. Пусть предметный и опорный источники лежат в одной плоскости (z₁ = z_r) и освещающая волна идентична опорной (x_c = x_r, z_c = z_r), тогда

x_3v = x_r (1 – ) + x₁, z_3v = z₁,

x_3R = x_r (1 + ) – x₁, z_3R = z₁. (4.33)

Оба изображения мнимые и расположены в той же плоскости, что и объект. Изображение с координатами (x_3R, z_3R) – перевернутое.