2.2.2.2 Виконання завдання

Визначаємо примусову складову напруги на ємності для часу

, а також та . Оскільки при ємність зарядиться, то її

внутрішній опір сталому струму буде рівним (рисунок 3) нескінченості . Тоді , .

За другим законом Кірхгофа

В,

тому

В.

За другим законом Кірхгофа для кола після комутації маємо

В. (2.6)

Складемо диференційне рівняння відносно напруги на ємності . Струм кола та напруга на активному опорі визначаються виразами (таблиця 2.1)

, .

Після підставлення цих виразів у співвідношення (2.6) отримаємо

В,

що становить шукане диференційне рівняння.

Розв’язувати це рівняння будемо на підставі виразу

. (2.7)

Складемо характеристичне рівняння та визначимо його корінь

.

Звідки . Отже

(2.8)

За наведеними вище значеннями параметрів стала кола дорівнює с.

Сталу інтегрування А визначимо шляхом підставлення у вираз (2.7) момент часу . Маємо або , звідки -61 В.

Після підставлення обчислених значень у вираз (8) знаходимо

В. (2.9)

На підставі даних таблиці 1 отриманий вираз дає змогу визначити закони зміни струму в колі та напруги на резисторі

А, (2.10)

В. (2.11)

2.2.3 Визначення перехідних та імпульсних характеристик відносно струму кола та напруг на його елементах і побудова їх графіків

2.2.3.1. Короткі відомості з теорії

Часові характеристики (перехідна та імпульсна) базуються на одиничній та дельта функціях.

Одинична (рисунок 2.4,а) функція (функція Хевісайда) визнача-ється виразом

.

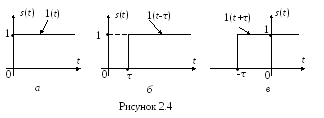
Розглядають одиничну функцію із запізненням (рисунок 2.4, б)

та випередженням (рисунок 2.4, в)

.

Одинична функція володіє двома важливими властивостями формування. Перша властивість полягає в тому, що при множенні неперервної функції (рисунок 2.5, а) на одиничну функцію (рисунок 2.5, б) формується розривна функція (рисунок 2.5, в), тобто

.

Друга властивість полягає в тому, що при множенні сталого числа А

(рисунок 6, а) на одиничну функцію (рисунок 6, б) формується ступінчаста

функція (рисунок 6, в), яку називають функцією вмикання, тобто

.

Дельта-функція (функція Дірака) – така функція, яка всюди дорівнює нулю, окрім моменту часу , де вона перетворюється в нескінченість (рисунок 2.7, а),тобто

Рисунок 2.5

Рисунок 2.6

. (2.12)

Дельта-функція може бути із запізненням (рисунок 2.7,б)

та із випередженням (рисунок 7, в)

.

Дельта-функція відноситься до узагальнюючих чи особливих функцій

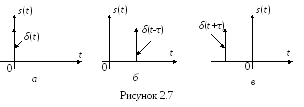
становить собою зручну математичну модель таких процесів, що швидко протікають, як вмикання та вимикання напруги, вибух, удар і т. п. Разом з тим інтеграл від цієї функції (що характеризує, наприклад, роботу струму чи сили) повинен відрізнятись від нуля.

Прикладом таких явищ може бути коротке замикання в електричному колі, коли струм в ньому практично миттєво зростає дуже великого значення, а потім швидко зменшується до нуля. Такий процес супроводжується значними затратами енергії. Для математичного опису таких імпульсних процесів використовується дельта-функція.

Розглядають три властивості дельта-функції.

Перша властивість полягає в тому, що

, (2.13)

тобто площина, обмежена дельта0функцією, дорівнює одиниці.

Математично вирази (2.12) та (2.13) є несумісними (за класичним визначенням інтеграл від функції (2.1) не існує). Тому дану властивість можна розглядати як границю прямокутного імпульсу тривалістю (рисунок 2.8) та амплітудою при .

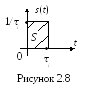
Дійсно, площина такого імпульсу дорівнює

,

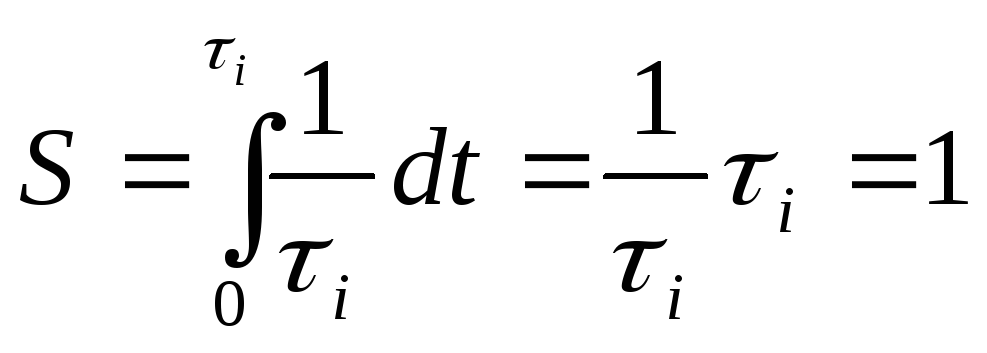а границя .

Таким чином, дельта-функція становить собою імпульс нескінченно

малої тривалості та нескінченно великої амплітуди. Фізично це означає, що тривалість дельта-функції значно менше тривалості досліджуваного електричного кола, тобто і тривалості перехідного процесу, а амплітуда імпульсу є достатньою, щоб такий процес виник при його дії.

Друга властивість отримала назву фільтрації. Вона полягає в тому, що

або ,

тобто, якщо під інтегралом неперервна функція множиться на дельта-функцію, то значення неперервної функції стають рівними нулю за винятком тих, де дельта-функція є визначеною.

Третя властивість полягає в тому, що

або ,

тобто добуток неперервної функції на дельта-функцію дорівнює їх добутку в

точці визначення дельта-функції.

Між одиничною та дельта-функцією існує зв’язок, який визначається виразом

або .

Часові характеристики електричних кіл становлять собою відгуки цих кіл на типові дії – на одиничну функцію та дельта-функцію – при нульових початкових умовах. Відповідно розглядають перехідну та імпульсну характеристики.

Перехідною характеристикою називають відгук електричного кола на дію одиничної функції при нульових початкових умовах. Оскільки при , то і при . Це аналітично виражається множенням перехідної характеристики на одиничну функцію . Тут наявність множника тільки обмежує область існування функції від до , не впливаючи на характер її зміни.

Розмірність перехідної характеристики залежить від розмірності вхідної дії та відгуку і визначається відношенням розмірності вихідної величини до розмірності вхідної дії. Види перехідних характеристик залежно від розмірності вхідних та вихідних величин подано в таблиці 2.2.

По вигляду перехідної характеристики можна визначити деякі властивості та параметри електричних кіл.

Таблиця 2.2 – До поняття перехідної характеристики електричного кола

№ з/п	Вхідна дія	Вихідна величина	Назва перехідної характеристики	Позначення	Одиниця виміру
1			По напрузі		Безрозмірна
2			Прохідна провідність		См
3			Прохідний опір		Ом
4			По струму		Безрозмірна

Імпульсною характеристикою електричного кола називають його відгук на дію дельта-функції при нульових початкових умовах.

Оскільки при і дорівнює нулю, якщо та , то при . При може бути нерівною нулю. Це пояснюється тим, що в момент часу , тобто в момент електричного удару по електричному колу, який триває дуже малий час , в колі може накопичитись електрична чи магнітна енергія. Дія цієї енергії може викликати появу струмів чи напруг на виході кола, тобто імпульсна характеристика може не дорівнювати нулю і після . Вигляд залежить від параметрів та конфігурації електричного кола.

За виглядом імпульсної характеристики можна приймати рішення про деякі властивості та параметри електричного кола.

Оскільки дельта-функція визначається похідної від одиничної функції, то імпульсна характеристика є похідною від перехідної характеристики або з врахуванням області існування

.

Таким чином імпульсна характеристика електричного кола дорівноє першій похідній від перехідної характеристики.

Після диференціювання останнього виразу отримаємо

.

На підставі третьої властивості дельта-функції друга складова останнього виразу не буде дорівнювати нулю тільки при тобто

.

Таким чином можна визначити імпульсну характеристику при відомій перехідній характеристиці. В останньому рівнянні добуток визначає вільну складову перехідного процесу, а – його примусову складову. Отже перехідна характеристика забезпечує можливість опису як вільної, так примусової складової перехідного процесу, а імпульсна характеристика – тільки вільної складової.