1. Перевернутый маятник на каретке как объект управления

1.1 Описание объекта

Θ

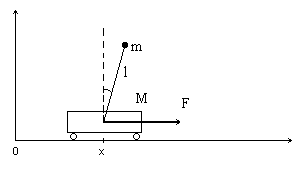
Рис 1.1

Принципиальная схема объекта управления.

На рис 1.1 представлен механический объект – маятник длины =1м с сосредоточенной массой m=1кг, отклоненный от положения равновесия на угол Θ=1рад, на движущейся под действием силы F каретке массой M=0.1кг, перемещенной от начала координат на x=1м.

Угловая скорость маятника =0.1рад/с, скорость каретки=0.1м/с.

Данная система имеет две степени свободы:

- поступательное движение каретки

- вращательное движение маятника

1.2 Математические модели объекты управления

Упущение: Если принять сосредоточенность масс; отсутствие трения и сопротивления воздуха, то математическая модель объекта может быть представлена в форме системы из двух дифференциальных уравнений:

Первое уравнение отображает второй закон Ньютона для вращающихся масс

(g=9.81 м/с²);

Второе уравнение – торой закон Ньютона для поступательного движения.

Реализация моделей в среде программы MatLabSimulinkупрощается, если уравнение записывается в форме Коши:

- четыре уравнения первого порядка, разрешенного относительно производных.

Для этого исходное уравнение разрешаем относительно старших производных.

Можно заметить, что исходное уравнение линейно, относительно и:

Пусть будет матрица:

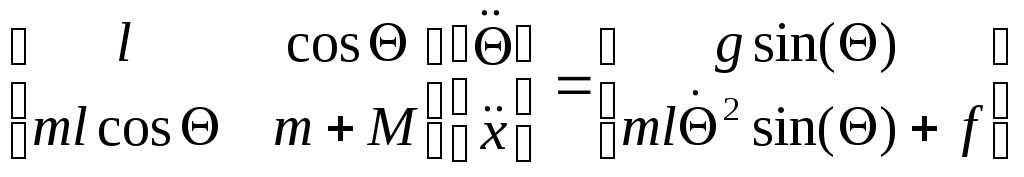
Уравнения имеют единственное решение, если определитель системы не равен 0:

Δ=l(m+M)-ml*cos²(Θ) ≠0;

Уравнения, разрешенные относительно старших производных примут вид:

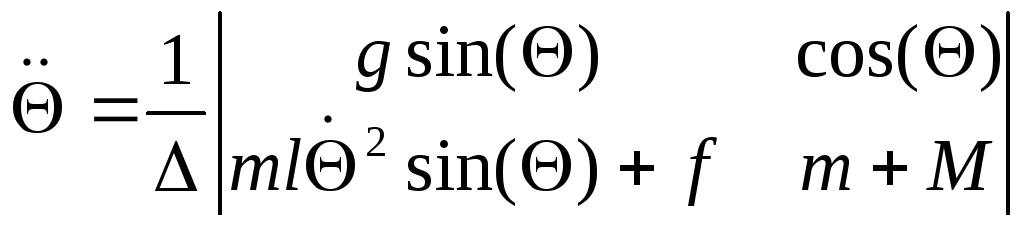
1.2.1 Нелинейные дифференциальные уравнения

Уравнения в форме Коши запишутся так:

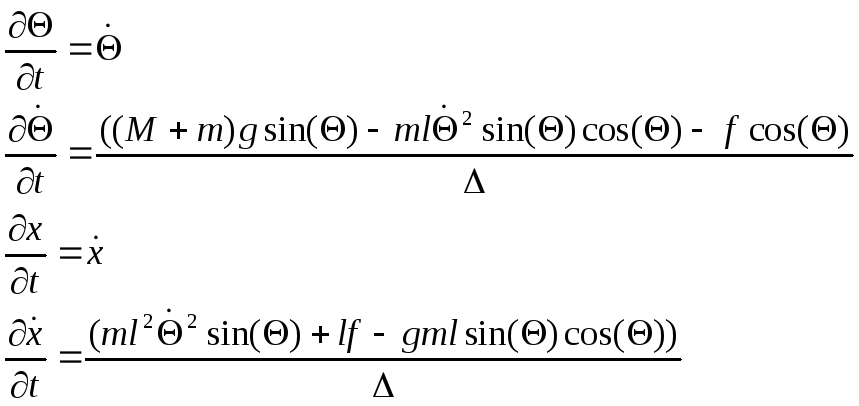
Уравнение дополняется начальными условиями.

1.2.2 Линеаризованные дифференциальные уравнение

Пусть просматриваются малые отклонения маятника от верхнего положения равновесия. При этом sin(Θ)≈Θ.

Мы заменим при этой линеаризации.

Рассмотрим малое отклонение маятника и малые угловые скорости.

Линеаризованные уравнения примут вид

Данный вариант задания конкретизирует параметры.

2. Анализ объекта управления

2.1 Компьютерная имитация объекта управления

Структурное представление моделей на языке графического редактора MatLabSimulinkизображено на рис 2.1. Реализуется на интеграторах.

Рис 2.1

Модель объекта на языке MatLab Simulink

Inital condition:

Integrator: 0.1

Integrator1: 1

Integrator2: 0.1

Integrator3: 1

2.2 Линеаризация компьютерной модели

Линеаризация моделей осуществляется автоматически по команде linmod2.

Матрицы задают модель в форме пространства состояний следующего вида:

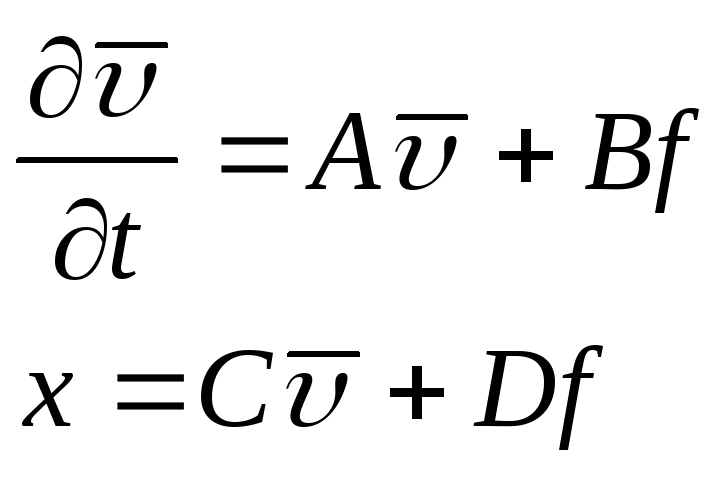
Аналитически с учетом принятых допущений см.1.2.2

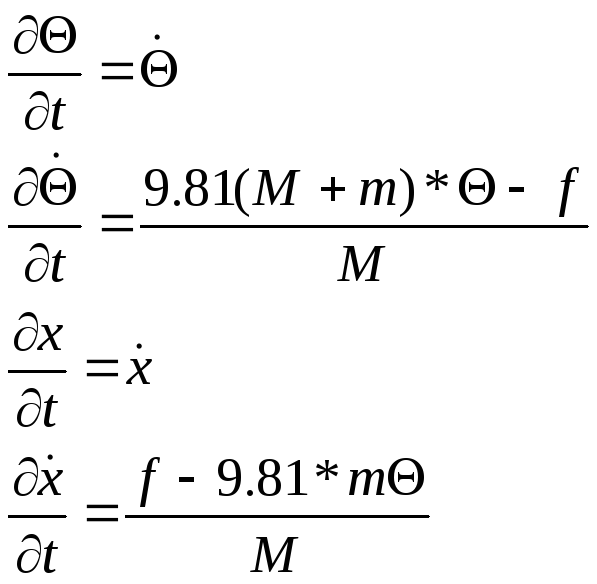
Следовательно,

- вектор состояния;R⁴

Команда linmod2 выбирает компоненты вектора состояния, не обязательно совпадающие с физическими переменными,,,

По структуре матриц A,B,C,Dпостараемся установить соответствие между абстрактными и физическими переменными состояния

>>[A,B,C,D]=linmod2(‘kursovik’)

A =

0 0 0 1.0000

0 0 1.0000 0

0 107.9100 0 0

0 -98.1000 0 0

B =

0

0

-10.0000

10.0000

C =

1 0 0 0

D =

0

По виду матрицы С делаем заключение, что x=u₁;D=0;По виду матрицAиBможно заключить:=u₄;;

Линеаризованное уравнение объекта в скалярной форме имеют вид: