3.5.2 Компьютерная имитация замкнутой системы

Подключаем линейный динамический регулятор к нелинейному объекту, как это покозано на рис 3.2

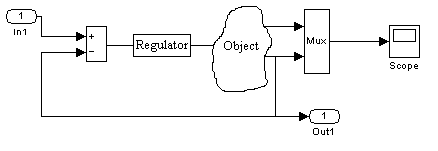
Рис 3.2

Структурная схема замкнутой системы

Целью имитационных исследований является оценка размеров области притяжения стабилизируемого положения равновесия.(При каких начальных отклонениях каретки маятник у нас вернется в состояние покоя.)

П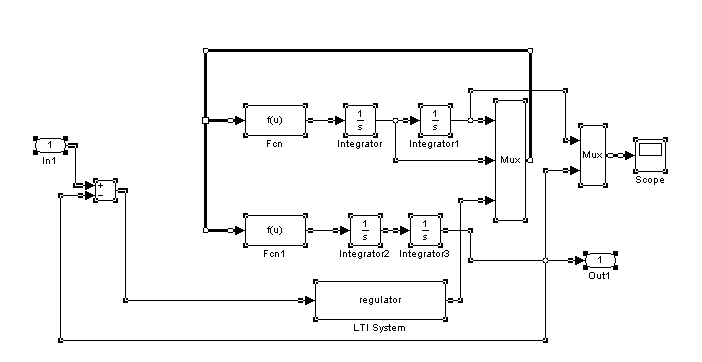режде всего убедимся в том, что положение равновесия устойчиво в малом. Для этого подвергнем линеаризации замкнутую систему.

Рис 3.2

Принципиальная схема замкнутой модели системы

>> [Ac1,Bc1,Cc1,Dc1]=linmod2('kurs')

Ac1 =

1.0e+003 *

0 0 0 0 0 0 0 0.0010

0 0 0.0010 0 0 0 0 0

0 0.1079 0 -1.3148 -0.0991 0.0026 0.0001 0

-0.1280 0 0 -0.1100 -0.0363 0.0166 0.0078 0

0 0 0 0.1280 0 0 0 0

0 0 0 0 0.0320 0 0 0

0 0 0 0 0 0.0080 0 0

0 -0.0981 0 1.3148 0.0991 -0.0026 -0.0001 0

Bc1 =

0

0

0

128

0

0

0

0

Cc1 =

1 0 0 0 0 0 0 0

Dc1 =

0

Проверим устойчивость, т.е вычислим собственные значения.

>> eig(Ac1)

ans =

-40.0000

-30.0000

-20.0000

-10.0000

-4.0000

-3.0000

-2.0000

-1.0000

Линеаризованная система устойчива, имеет желаемые собственные знпчения, что свидетельствует о существовании области устойчивости в малом (малой области устойчивости). Для оценки области притяжения проведем серию имитационных исследований, назначая различные начальные условия ,;

Получены следующие значения:

;

;

4. Синтез дискретного регулятора

4.1 Способы синтеза

Можно выделить два способа синтеза дискретного регулятора, стабилизирующего непрерывный объект:

1 – дискретизация непрерывного регулятора;

2 – синтез дискретного регулятора на базе дискретной модели объекта;

На рис 4.1 иллюстрируются оба способа.

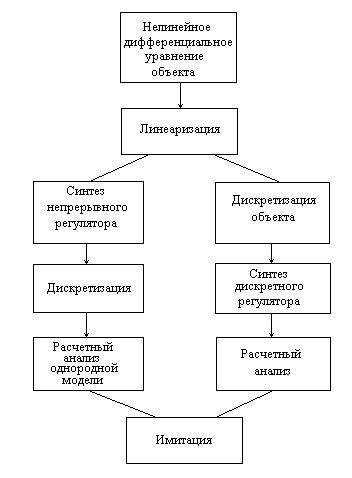
Рис 4.1

Способы синтеза дискретного регулятора

примечание: Имитация возможна только при существовании области устойчивости дискретной системы.

4.2 Дискретизация непрерывного регулятора

Основным вопросом при дискретизации непрерывного регулятора является выбор периода дискретизации Т. Имеются противоречивые требования – слишком малые значенияТусложняют техническую реализацию, а слишком большие – приводят к недопустимой потере информации, в результате чего замкнутая система может стать неустойчивой.

Период дискретизации Твыбирается «экспериментально», для выбора начального приближения можно воспользоваться теоремой Котельникова – Шеннона, которая утверждает, что частота дискретизации должна быть более чем в два раза выше максимальной частоты в спектре сигнала.

Спектр сигналов (распределение энергии по частотам) циркулирующих в контуре регулирования и в контуре наблюдающего устройства, определяются собственными значениями, которые были назначены при синтезе.

Положим, что максимальная частота в спектре сигналов в пять раз выше максимального модуля собственных значений (р)

w_max=5|p_i|;

В нашем случае |p_i| = 40c^-1;

Значит,w_max = 5*40 = 200c^-1;

Приближенное значение периода дискретизации находится так: w_T>2 w_max; w_T>400c^-1

w_T= >400c^-1;T<0.0157; Т≈0.015;

Проведем дискретизацию полученного ранее непрерывного регулятора по команде:

>>[Ard,Brd,Crd,Drd]=c2dm(Ar,Br,Cr,Dr,0.015)

Ard =

0.1023 0.0031 0.0010 0.0072

4.6869 1.0075 0.0170 0.0454

37.6796 -0.4188 0.8203 0.3412

-17.8233 0.6164 0.1969 0.8588

Brd =

0.8979

-4.6866

-37.7082

17.8544

Crd =

-0.2446 -14.5356 -1.5097 -0.5097

Drd =

0

Проведем расчетный анализ системы с дискретным регулятором. Расчетные методы имеются только для однородных объектов, поэтому подвергнем дискретизации и объект:

>> [Ad,Bd,Cd,Dd]=c2dm(A,B,C,D,0.015)

Ad =

1.0000 -0.0111 -0.0001 0.0150

0 1.0122 0.0151 0

0 1.6252 1.0122 0

0 -1.4775 -0.0111 1.0000

Bd =

0.0011

-0.0011

-0.1506

0.1506

Cd =

1 0 0 0

Dd =

0

Рис 4.2

Структурная схема дискретной модели замкнутой системы

Получим матрицы замкнутой системы:

>> [Acd,Bcd,Ccd,Dcd]=feedback(Ad,Bd,Cd,Dd,Ard,Brd,Crd,Drd)

Acd =

1.0000 -0.0111 -0.0001 0.0150 0.0003 0.0164 0.0017 0.0006

0 1.0122 0.0151 0 -0.0003 -0.0164 -0.0017 -0.0006

0 1.6252 1.0122 0 -0.0368 -2.1892 -0.2274 -0.0768

0 -1.4775 -0.0111 1.0000 0.0368 2.1884 0.2273 0.0767

0.8979 0 0 0 0.1023 0.0031 0.0010 0.0072

-4.6866 0 0 0 4.6869 1.0075 0.0170 0.0454

-37.7082 0 0 0 37.6796 -0.4188 0.8203 0.3412

17.8544 0 0 0 -17.8233 0.6164 0.1969 0.8588

Bcd =

0.0011

-0.0011

-0.1506

0.1506

0

0

0

0

Ccd =

1 0 0 0 0 0 0 0

Dcd =

0

>>eig(Acd)

ans =

0.1047

1.0174 + 0.3118i

1.0174 - 0.3118i

0.7603

0.9540

0.9618

0.9987 + 0.0134i

0.9987 - 0.0134i

>>abs(eig(Acd))

ans =

0.1047

1.0641

1.0641

0.7603

0.9540

0.9618

0.9988

0.9988

Причиной неустойчивости замкнутой дискретной системы может быть слишком большой период времени дискретизации. Чтобы проверить это предположение, повторим дискретизацию и анализ изменяя значения Т;

Вывод: Замкнутая линейная система при Т≈0.01 является устойчивой, что свидетельствует о существовании области притяжения положения равновесия.

Проведем имитационное исследование гибридной системы образованной нелинейным непрерывным объектом и линейным дискретным регулятором для оценки размеров области притяжения.

;

;

При уменьшении Т до 0.0001с не существует области устойчивости.

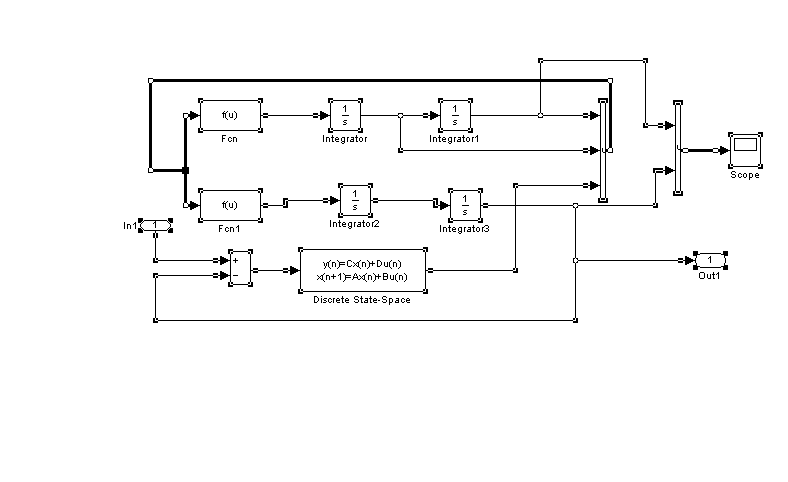
Рис 4.3

Принципиальная схема дискретной модели замкнутой системы

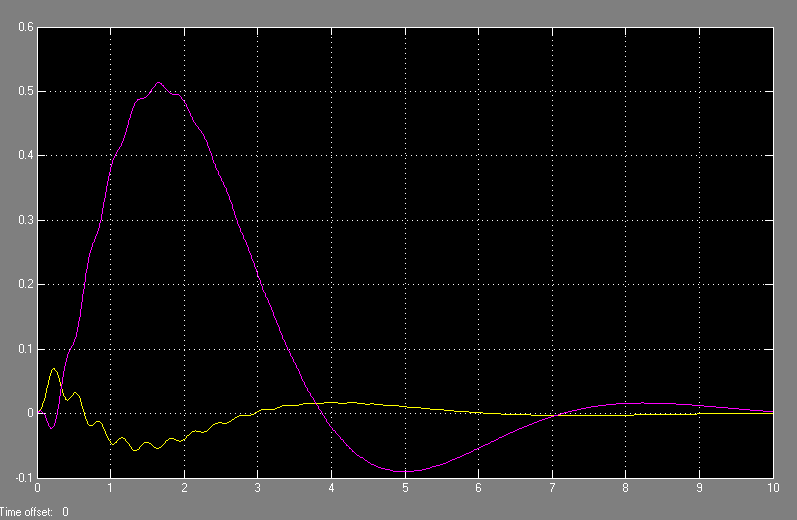
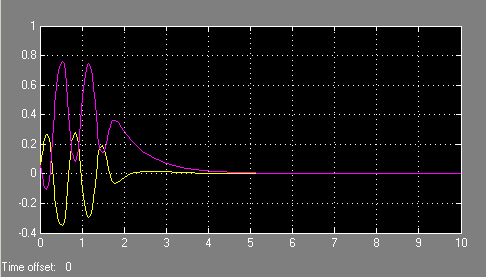
Рис 4.4

График переходных процессов замкнутой системы,

дискретизированой по времени Т=0.01 с