При получении дополнительных условий

_max<=25-30%;

t_р<=0,2 с; определим частоты для построения желаемой ЛАХ:

ω_e<ω_ср< ω_к

По диаграмме Солодовникова определяем частоту среза w_ср

=54,95; lgw_ср=1.67

40<54,95<400

ω_к =D_ω= 400 lgω_к=2.6

ω_е=_e = =6,32 lgω_е= 0.95

0.95<1.67<2.6

Построим желаемую ЛАХ (Рис.2)

Рис.2 Построение желаемой ЛАХ

W_к ==

Построим ЛАХ корректирующего устройства

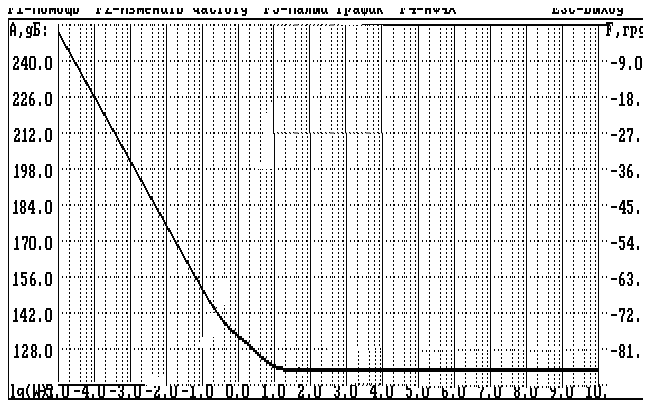
Рис.3 ЛАХ корректирующего устройства

По ЛАХ корректирующего устройства выбираем схему корректирующего устройства.

;

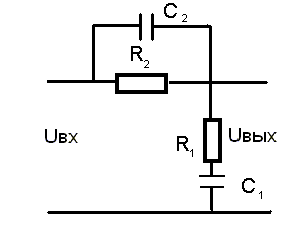
Произведем расчет элементов корректирующего устройства

1) Т=T=0,2

T=0,6

T=Т=1

Т=Т=0,002

Пусть С=10мкФ, тогда

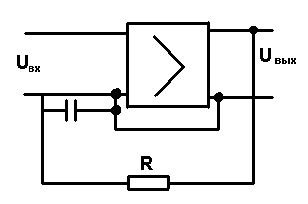
W(P)=

T=RC

Пусть С=10Мкф, тогда

R=T/C=2,602/10=0.2602кОм

Построим переходный процесс синтезированной системы

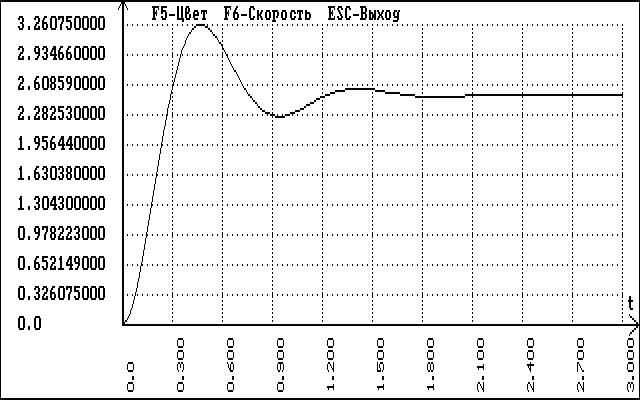
Рис.4 Переходный процесс синтезированной системы

Рис.5 Ошибка синтезированной системы

По графику (Рис.4) определим основные показатели качества.

1.Максимальное перерегулирование.

σ =(х_max-х_вын)*100%/х_вын=(3.26-2.28)*100%/50=1.96%.

2. Время регулирования.

t_р=1,8с.

3.Число колебаний t_k=1.

4. Собственная частота колебаний.

w=2П/t_k=2*3.14/2=3.14.

5. Логарифмический декремент затухания.

d=ln(q_i/q_i+1)=ln(0.327/0.103)=1.155.

6. Максимальная скорость отработки сигнала.

[dx/dt]_max=1,22

Построим ЛАХ и ЛФХ разомкнутой части синтезированной системы

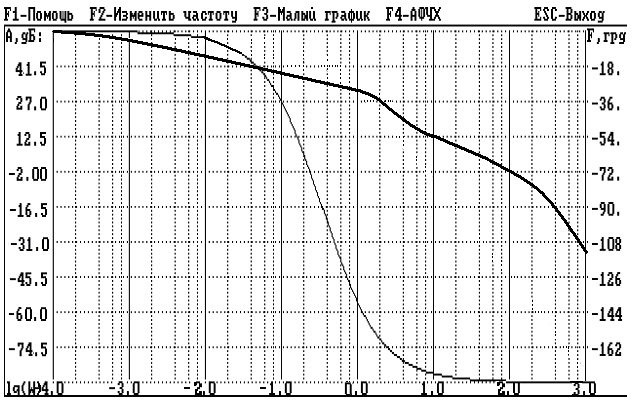
Рис.6 ЛАХ и ЛФХ синтезированной системы

Заключение

По заданной конструктивной схеме составили функциональную схему и динамическую модель исследуемого объекта в виде системы дифференциальных уравнений. Составили структурную схему и реализовали ее на ЭВМ. Определили показатели качества системы. Провели синтез САР с учетом дополнительных условий. Проанализировав полученную систему удостоверились, что она удовлетворяет заданным требованиям.

Используемая литература

1. Теория автоматического управления: Учеб. для вузов по спец. “Автоматика и телемеханика”. В 2-х ч. Ч.I. Теория линейных систем автоматического управления/ Н.А. Бабаков, А.А. Воронов, А.А. Воронова и др.; Под ред. А.А. Воронова.—2-е изд., перераб. и доп.—М.: Высш.шк.,1986.—367с.,ил.

2. В.В. Семенов, А.В. Пантелеев, А.С. Бортовский. Математическая теория управления в примерах и задачах. – М.: МАИ, 1997.