курсовая работа / курсач часть 2 ирине !...!...!... вар 2

2 Исследование НЕлинейной сАР

2.1 Техническое задание

– передаточная функция бака;

- передаточная функция всасывающего клапана;

- передаточная функция насоса;

- передаточная функция гидроцилиндра;

- передаточная функция золотника.

Рисунок 7 – Структурная схема нелинейной системы автоматического регулирования с нелинейным элементом

График, описывающий нелинейный элемент Н.Э. приведен на рисунке 8

Рисунок 8 – Релейная статическая характеристика

2.2 Упрощение структурной схемы нелинейной системы автоматического регулирования

Применяя правила преобразования структурных схем, упростим схему, изображенную на рисунке 7.

Рисунок 9 - Итоговое преобразование системы автоматического регулирования с нелинейным элементом

Где

Определим передаточную функцию:

3. Построение фазового портрета нелинейной системы автоматического регулирования

Об устойчивости системы будем судить по фазовому портрету. Построение фазового портрета будем вести методом припасовывания. Но, сначала рассмотрим данную нам нелинейную характеристику элемента с ограничениями.

Из рисунка 8 следует:

По определению передаточной функции имеем:

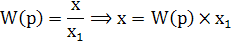
Подставляя в эту формулу значение передаточной функции получим:

В знаменателе и числителе данной передаточной функции выражения в седьмой степени, то есть характеристическое уравнение линейной части нелинейной САР имеет пятую степень.

Степени больше второй - степени для более низких частот, оказывают небольшое влияние на систему в целом, поэтому мы можем ими пренебречь.

Следовательно можем записать, что:

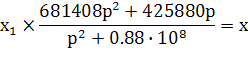
Приведенную формулу можно записать в виде:

Воспользуемся пакетом MathCad для решения этого дифференциального уравнения.

Введем замену и исключим из правой части уравнения производную:

Перенесем влево:

Так как в качестве нелинейного элемента используется реле со статической характеристикой, представленной на рис.8, то подставляя значение для трех участков, получим систему:

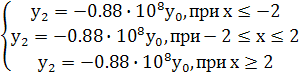
Создадим матрицу для решения дифференциального уравнения в программе MathCad:

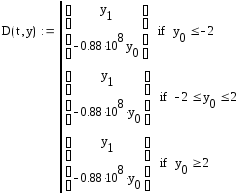
В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицы для трех начальных условий:

Возьмем количество точек равным 100000 и конечное время интегрирования 15, то матрица решений запишется как:

Построим фазовый портрет:

Рисунок 10 – Фазовый портрет нелинейной системы

Построим переходные процессы нелинейной системы.

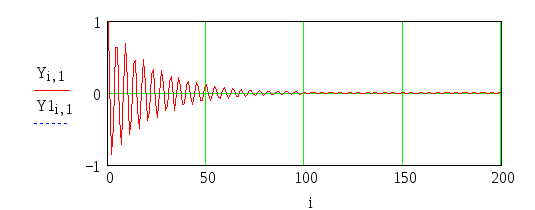
Рисунок 11 – Переходный процесс нелинейной системы

Вывод.

На рисунке 10 представлен фазовый портрет нелинейной системы. Из графика видно, что при различных начальных условиях система будет оставаться устойчивой. С течением времени процесса амплитуда колебаний будет уменьшаться, система придет к устойчивому равновесию – точке (0;0) на рисунке 10, то есть произойдет процесс переключения. Устойчивость системы подтверждает график переходного процесса рисунок 11.

22

УИТС.421241.232 ПЗ

Дата

Подп.

№ докум.

Лист

Изм.

Лист