Реализация математической модели цифровой системы в переменных состояния с помощью пакетов MatLab, MathCad.

Для реализации модели в переменных состояния с помощью пакета MathCAD используем разностные уравнения, которые можно рассчитать по синтезированной структурной схеме с вводом новых переменных (рис. 11):

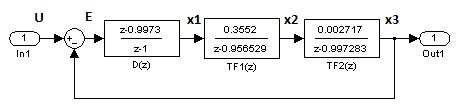
рис. 11

Запишем уравнения для каждого элемента входящего в систему.

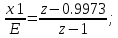
Преобразуем полученные уравнения в линейные, используя замену: X*Z -> X(n+1), X ->X(n). Перенесём переменные с (n) вправо, с (n+1) влево.

Переносим найденные уравнения в MathCAD:

Результат выполнения программы на рис. 12.

рис. 12

Не трудно заметить, что график вышел из 5%-ной зоны, то есть какие-то переменные были некорректно округлены. Этого можно избежать находя z-изображения через прямое z-преобразование того же MathCAD. Однако система осталась устойчива, перерегулировка невелика, по этому считаем результат достигнутым.

Теперь построим модель в переменных состояния. Для этого найдём передаточную функцию всей системы:

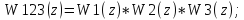
Передаточная функция разомкнутой системы W123:

Передаточная функция замкнутой системы Ws:

Найденная передаточная функция показывает связь между входом и выходом системы:

Отсюда разностное уравнение во временной форме:

Z-изображение управляемой величины:

Структурная схема ЦСАУ в переменных состояния показана на рис. 13.

b0

a0

b1

Σ

a1

Σ

a2

u(n)

x3(n) x2(n) x1(n)

Σ

рис. 13

По структурной схеме записываем разностные уравнения:

Матрицы состояния:

В нашем уравнении:

a2 = -2.953812; a1 = 2.908705; a0 = -0.954890;

b1 = 0.0009633; b0 = -0.0009607;

Смоделируем систему в приложении Simulink (рис. 13-14):

График переходной функции совпадает с графиками полученными при создании аналоговых моделей. Система устойчива и не выходит и допустимой зоны перерегулирования.

рис. 13

Рис. 14

Выводы: сравнение синтезированных аналоговой и цифровых систем.

В ходе курсовой работы были синтезированы несколько математических моделей одной и той же системы. Сравним результаты полученный каждой математической моделью с исходной аналоговой с помощью Simulink (рис. 15).

рис. 15

На входы осциллографа подаются такие сигналы:

1. Чисто аналоговая система (жёлтая линия).

2. Аналоговая система с дискретным регулятором (розовая линия).

3. Чисто дискретная система (голубая линия).

4. Дискретная система в пространстве состояний (красная линия).

5. Максимально допустимый уровень перерегулировки +5% (синяя линия).

6. Уровень единичного сигнала (зелёная линия).

Модели дают практически одинаковый результат – система устойчива и укладывается в 5%-ный диапазон перерегулирования.

рис. 16

Модели дают практически одинаковый результат – система устойчива и укладывается в 5%-ный диапазон перерегулирования.

рис. 17

Масштабируя графики видим следующий результат (рис. 17): при переходе от аналоговой модели к дискретной, кривая переходного процесса «уплывает». Первые потери происходят после замены аналогового регулятора дискретным. Ещё большие потери –после замены остальных аналоговых элементов дискретными эквивалентами. При дальнейшей работе с дискретной схемой (например переход от модели пространства сигналов к модели в пространстве состояний) погрешность не увеличивается – голубой и красный график совпадают. Следовательно, ошибки вносятся на этапе z-преобразования. Для получения точных значений и соответственно качественных эквивалентных схем, этому этапу следует уделить особое внимание и производить вычисления с как можно более высокой точностью.

22