5. Построение графика переходного процесса и оценка качества

скорректированной системы

5.1 Моделирование системы на авм

Исходным выражением для моделирования является передаточная функция разомкнутой скорректированной системы W_ск(р).

Составим аналоговую модель системы на основании моделей типовых динамических звеньев. Схема модели приведена на рисунке 7.

Рассчитаем машинные коэффициенты модели.

Машинные коэффициенты преобразующего элемента:

Машинные коэффициенты корректирующего устройства:

Машинные коэффициенты управляющего устройства:

Машинные коэффициенты исполнительного устройства:

Машинные коэффициенты объекта управления:

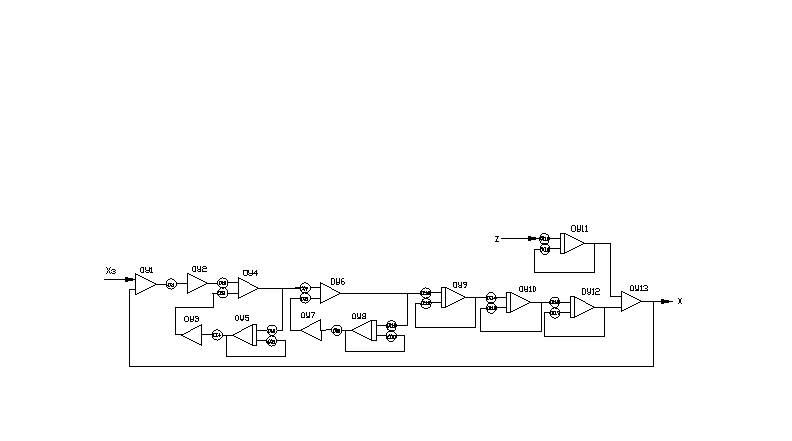Рисунок 7 - Схема аналоговой модели системы

2. Моделирование системы на ЦВМ

Для цифрового моделирования системы используем среду MatlabприложениеSimulink. Схема цифровой модели системы, составленная из типовых звеньев библиотекиSimulink, показана на рисунке 8.

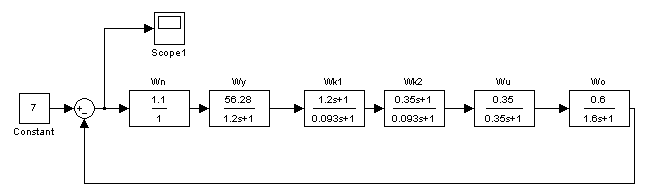
Рисунок 8 - Схема цифровой модели системы

Результатом моделирования является переходная характеристика по каналу ошибки x_з– ε , регистрируемая приборомScope1. Переходная характеристика системы по каналу ошибкиx_з– ε приведена на рисунке 9.

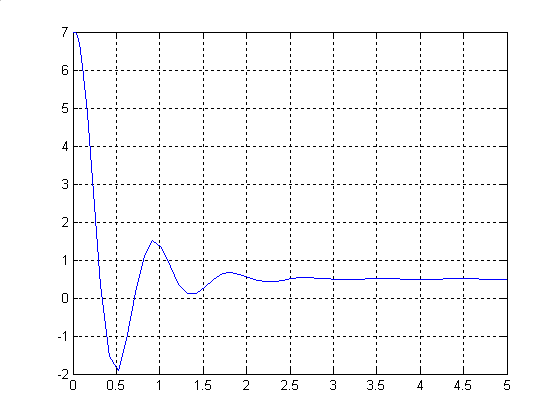
Рисунок 9 - Переходная характеристика системы по каналу ошибки x_з– ε

По графику переходного процесса определим перерегулирование, время переходного процесса и сравним полученные значения с заданными.

ε(∞)=0,5 - что удовлетворяет заданию

6. Вычисление и минимизация квадратичной интегральной оценки

при типовом воздействии

Исходным выражением для вычисления квадратичной интегральной оценки является передаточная функция замкнутой скорректированной системы по каналу х_з-ε при единичном ступенчатом воздействии (то есть принимаем задающее воздействие Х_з(t)=1, а следовательно Х_з(р)=1/р). Запишем эту передаточную функцию:

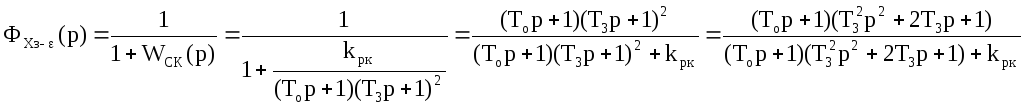
Раскроем скобки и приведем передаточную функцию к стандартному виду:

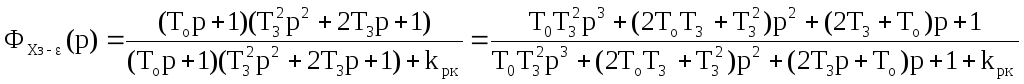
Подставим в формулу численные значения:

Запишем выражение для изображения переходной составляющей сигнала ошибки:

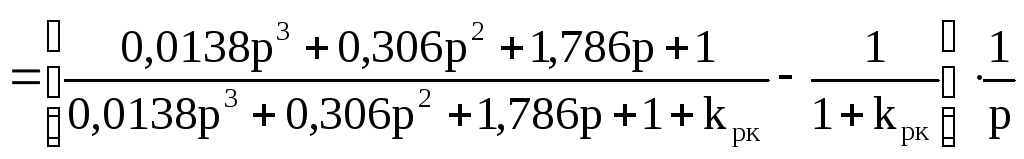
Так как передаточный коэффициент разомкнутого контура k_рк≥10 допускается упростить выражение для изображения переходной составляющей с учетом следующих условий:

k_рк+1=k_ркиk_рк-1=k_рк

Преобразуем выражение для изображения переходной составляющей сигнала ошибки, используя вышеприведенные условия:

=

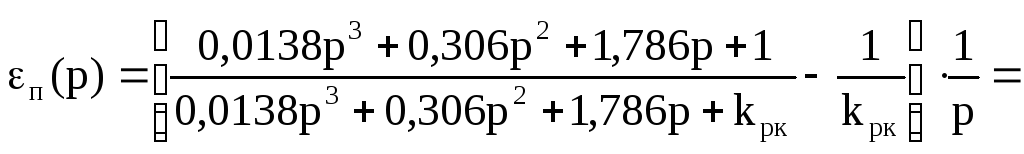
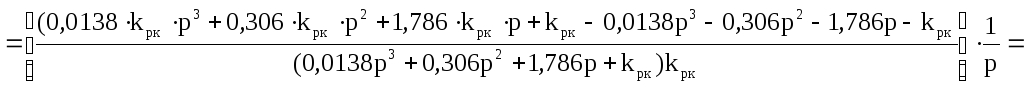
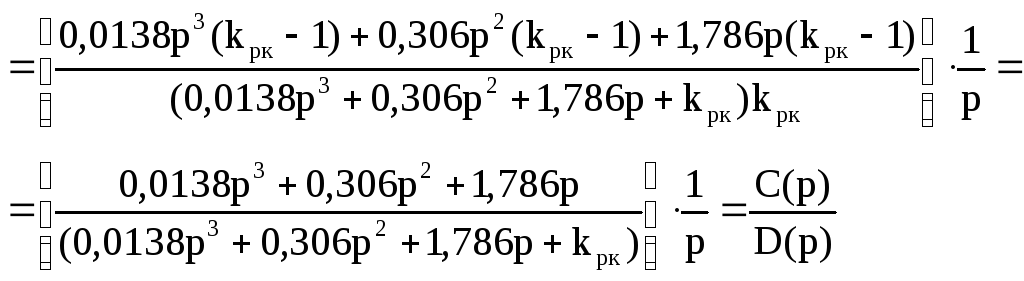
Для вычисления квадратичной оценки по изображению используют равенство Парсеваля, которое имеет вид:

Где

Таким образом коэффициенты d_iиv_iравны:

d_o =0,0138 v_o =0,00019

d₁ =0,306 v₁ =-0,143

d₂ =1,786v₂ =3,19

d₃ = k_рк

Составим определитель Δ по правилу составления определителя Гурвица

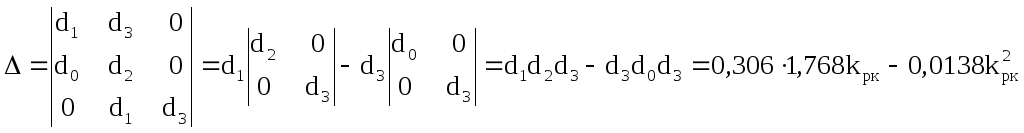
Определитель _vсоставляем из определителяпутем замены коэффициентов верхней строки на коэффициенты₀,₁и₂.

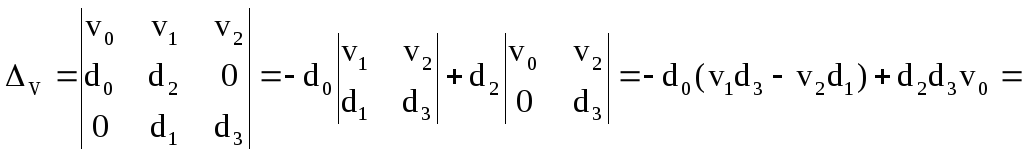
Вычисляем квадратичную интегральную оценку:

Задаваясь численными значениями k_рк, составляем таблицу зависимости квадратичной интегральной оценки от коэффициентаk_рк, которая приведена ниже.

Таблица 3. – Расчетные данные для построения кривой зависимости интегральной оценки от передаточного коэффициента разомкнутого контура

kрк	Qкв
0	∞
1	1,039
2	0,63
5	0,37
8	0,325
10	0,317
10,5	0,366
10,56	0,3165
11	0,31,68
12	0,3174
20	0,39
24	0,47

Рисунок 9 - Кривая зависимости интегральной оценки от передаточного коэффициента разомкнутого контура

Из рисунка 9 видно, что оптимальным значением k_ркявляетсяk_рк=10,56. При данном значении коэффициента разомкнутого контура система будет работать в оптимальном режиме, обеспечивая минимальную площадь под графиком переходного процесса.

Теперь перейдем от коэффициента k_ркк передаточному коэффициентуk_у. Для этого воспользуемся следующей формулой:

При коэффициенте k_рк=12,96 и квадратичной интегральной оценке равнойQ=0.3218 передаточный коэффициент управляющего устройстваk_у.= 56,28.

Вывод: В этом разделе с помощью квадратичной интегральной оценки получили оптимальное значение передаточного коэффициента управляющего устройства (k_у=45,8). Этот коэффициент получился меньше, чем тот, что был выбран в разделе 2 (k_у=56,28). Следовательно, при выборе этого коэффициента точность системы в установившемся режиме увеличится, но могут получиться более колебательные переходные процессы.

7. Вычисление и минимизация дисперсии сигнала ошибки при случайных воздействиях

Дисперсия сигнала ошибки D_при действии на систему внешних некоррелированных воздействий х_зиgможет быть представлена суммой:

где D_з– дисперсия, обусловленная неточным воспроизведением задающего воздействия;

D_eg– дисперсия, обусловленная неполным подавлением помех.

Вычислим дисперсию, обусловленную неточным воспроизведением задающего воздействия:

где S_хз(ω) – спектральная плотность полезного сигнала

Запишем передаточную функцию замкнутого контура по каналу ошибки х_з-х.

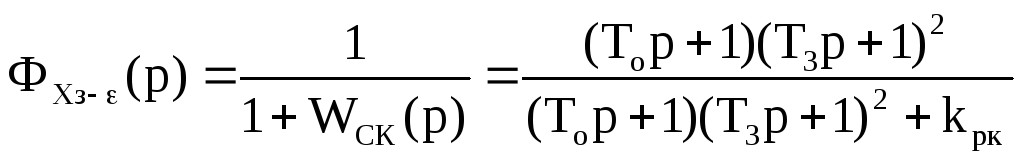
Заменяем оператор р на jω:

Подставим это выражение в формулу дисперсии, обусловленной неточным воспроизведением задающего воздействия:

=

==

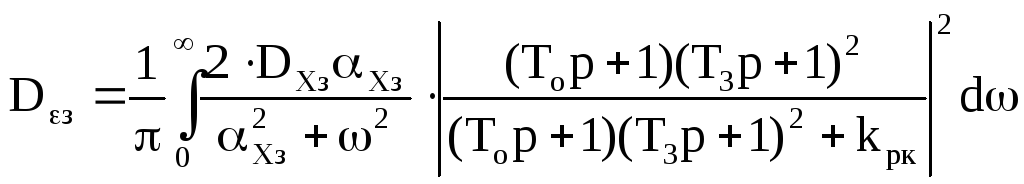
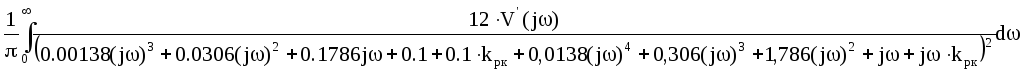
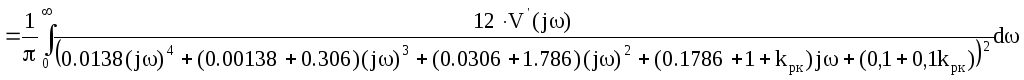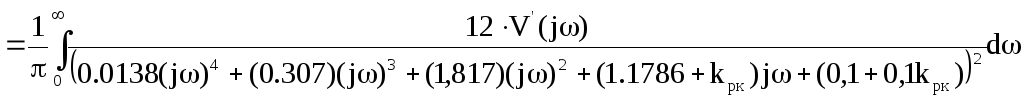
где

Подставим это выражение в формулу дисперсии, обусловленной неточным воспроизведением задающего воздействия:

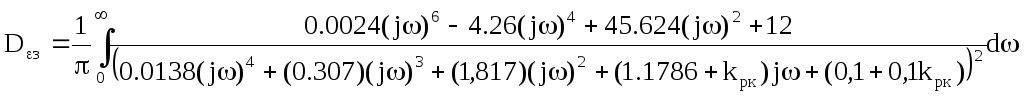
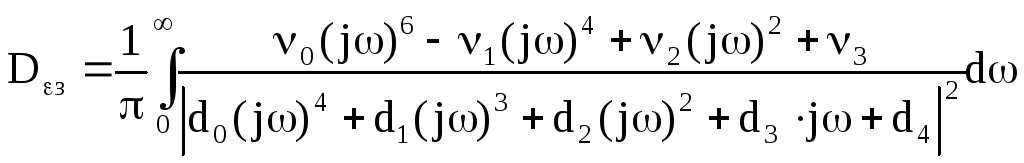
Вычисление дисперсии неточного задающего воспроизведения вычислим по формуле:

Запишем коэффициенты v_iиd_i для составления определителей Δ и Δ_v :

v₀=0.0024d₀=0.0138

v₁=-4.26d₁=0.307

v₂=45.624d₂=1.817

v₃=12d₃=1.1786+k_рк

d₄=0,1+0,1k_рк

Определитель составляется из коэффициентовd_iпо правилу составления определителя Гурвица.

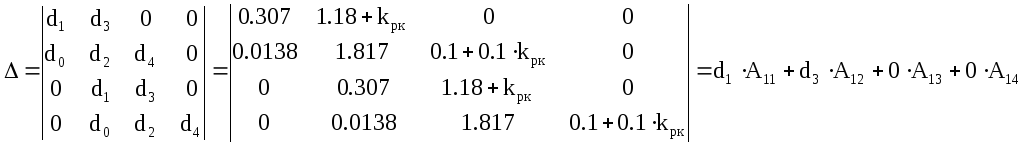
Определитель Δ_v составляем путем замены коэффициентов верхней строки матрицы Δ на коэффициентыv_i .

где А_ij - алгебраические дополнения элементов определителя

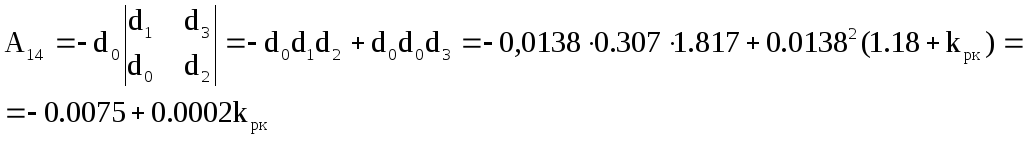
Подставим значения алгебраических дополнений в формулы определителей Δ и Δ₁ .

=

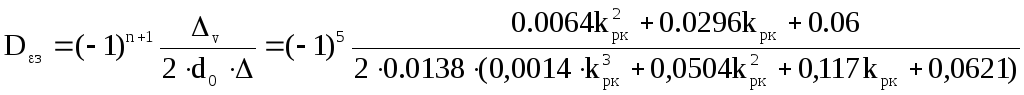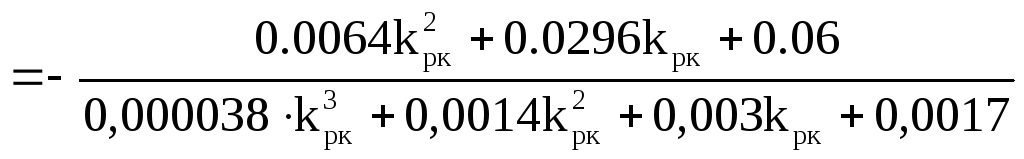
Далее вычислим дисперсию, обусловленную неполным подавлением помехи:

где S_g() – спектральная плотность помехи

=120

Запишем передаточную функцию скорректированной системы по каналу «g-»:

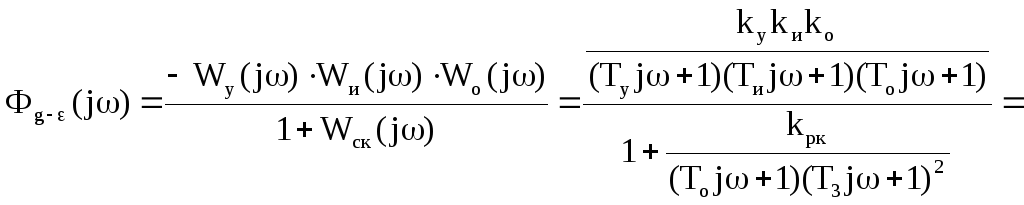
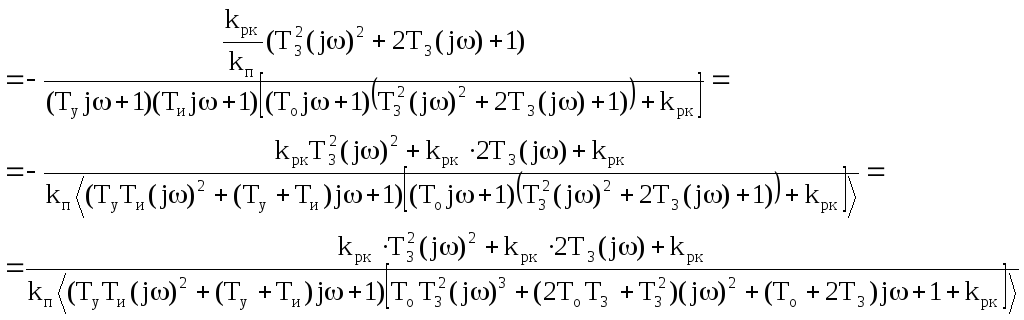
Отдельно раскроем скобки и приведем подобные члены знаменателя, после чего подставим численные значения постоянных времени.

Подставим численные значения в формулу передаточной функции скорректированной системы по каналу «g-»:

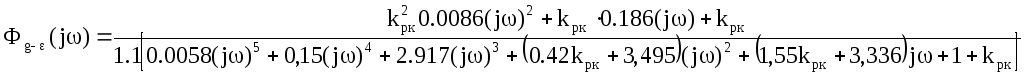
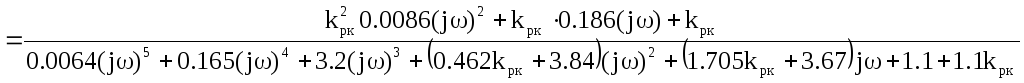
Далее подставим передаточную функцию системы по каналу «g-» в формулу дисперсии неполного подавления помехи:

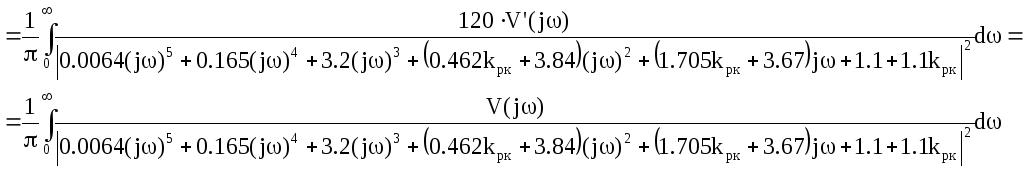
где

Подставим это выражение в формулу дисперсии неполного подавления помехи:

По согласованию с преподавателем упрощаем подынтегральное выражение неполного подавления помехи до следующего:

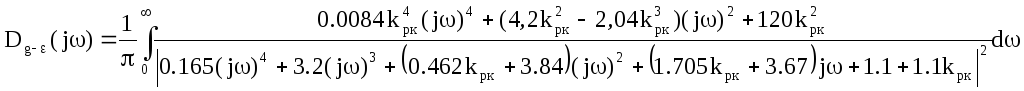
Вычисление дисперсии неполного подавления помехи вычислим по формуле:

Запишем коэффициенты v_iиd_i для составления определителей Δ и Δ_v :

v₀=0d₀=0,165

v₁=0,0084d₁=3,2

v₂=4,2-2,04d₂=0,462k_рк+3,84

v₃=120d₃=1.705k_рк+3,67

d₄=1,1+1,1k_рк

Определитель составляется из коэффициентовd_iпо правилу составления определителя Гурвица.

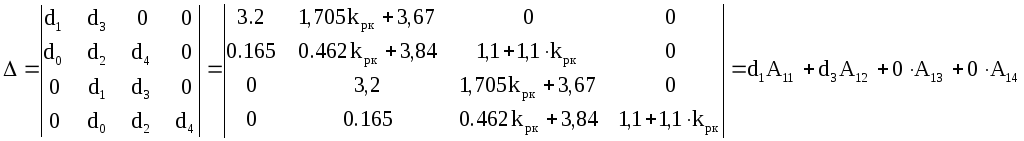
Определитель Δ_v составляем путем замены коэффициентов верхней строки матрицы Δ на коэффициентыv_i .

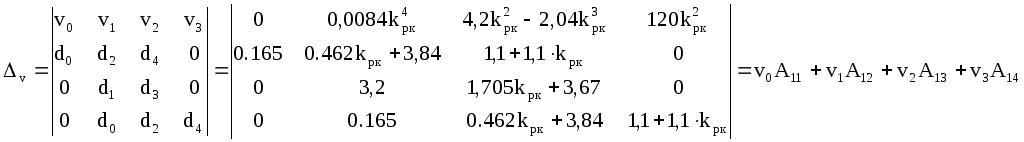где А_ij - алгебраические дополнения элементов определителя

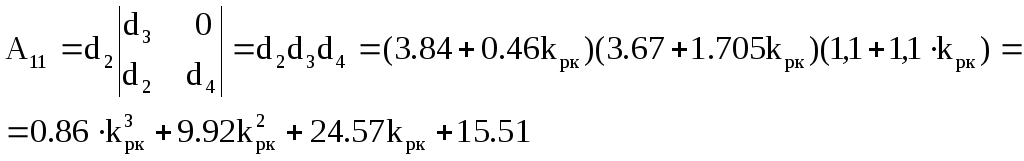
Подставим значения алгебраических дополнений в формулы определителей Δ и Δ₁ .

=

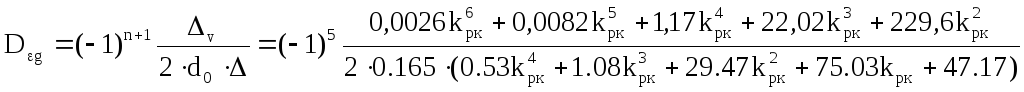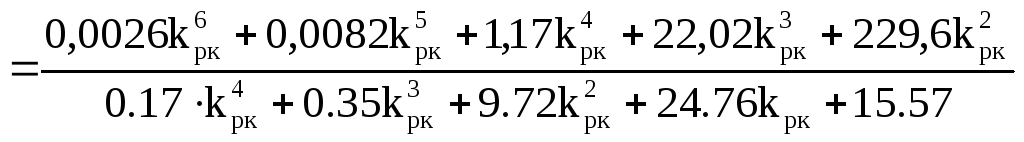
В соответствии с найденными аналитическими выражениями дисперсии неточного задающего воспроизведения и неполного подавления помехи составим таблицу для построения графиков D_εз =f(k_рк) иD_gε =f(k_рк), а также суммарного графикаD_ε =f(k_рк).

Таблица 4 - Расчетные данные для построения графиков зависимости дисперсии от передаточного коэффициента разомкнутого контура

kрк	Dεз	Dgε	Dε
0	41.17
0.5	23.52
1	16.36
1.92	9.89
2	9.48
3	6.45
4	4.81
5	3.81
8	2.3
10	1.81
12	1.5
12.92	1.39

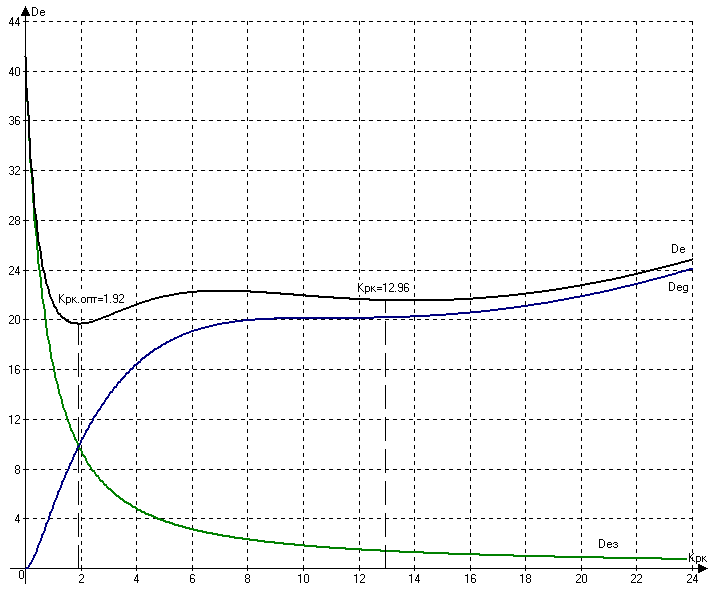
Рисунок 10 - Графики зависимости дисперсии сигнала ошибки скорректированной системы от передаточного коэффициента разомкнутого контура

Как видно из рисунка 10 оптимальным значением передаточного коэффициента разомкнутого контура является k_рк =1,92 , при котором дисперсия сигнала ошибки минимальна (D_=19,9.)

Перейдем от коэффициента k_ркк передаточному коэффициенту управляющего устройстваk_у. Для этого воспользуемся следующей формулой:

Вывод: Для оптимальной работы системы по суммарной дисперсии сигнала ошибки необходимо передаточный коэффициент разомкнутого контура принять равным 1,92 , из чего следует, что передаточный коэффициент управляющего устройства должен быть равен 8,31. Но при таком значении коэффициента управляющего устройства заданная точность управления системы не будет достигнута. В то же время как видно из рисунка 10 при коэффициенте k_рк =12,96 на графике суммарной дисперсии сигнала ошибки наблюдается прогиб, из чего следует что при данном коэффициенте разомкнутого контура при случайном входном воздействии, оказываемом на систему значение дисперсии будет достаточным для обеспечения заданной точности управления.