2.3 Построение фазового портрета

Передаточная функция есть 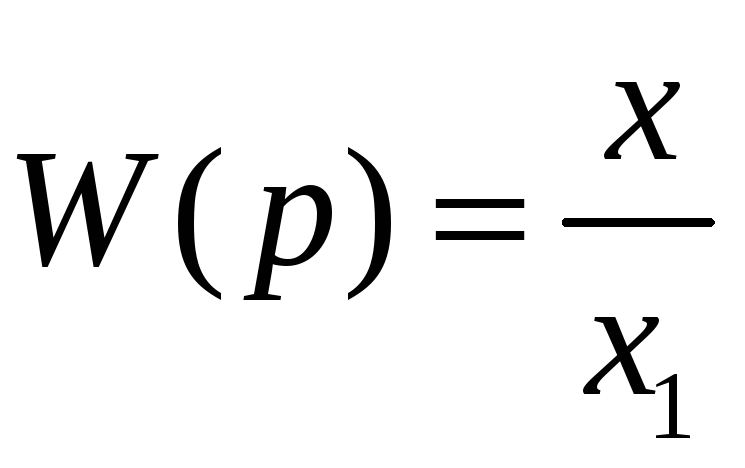или ,

где -передаточная функция линейной системы;

Подставляя в эту формулу значение передаточной функции получим:

Приведенную формулу можно записать в виде:

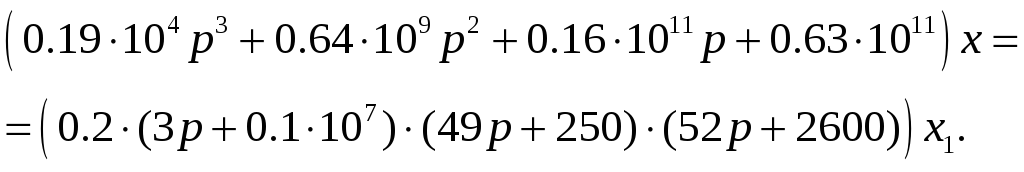
Воспользуемся пакетом MathCad для решения этого дифференциального уравнения.

Введем замену и исключим из правой части уравнения производную:

Для того чтобы построить фазовый портрет, необходимо, чтобы степень числителя и знаменателя не превышала вторую степень, поэтому элементы выше второй степени исключаем. Тогда получим:

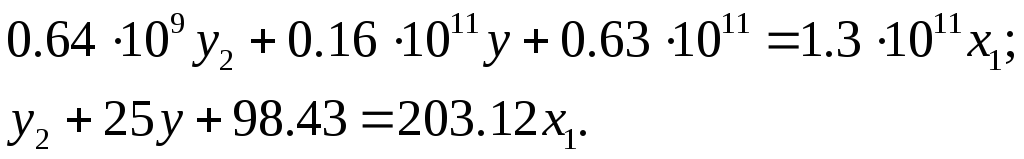
Так как в качестве нелинейного элемента используется реле с гистерезисом со статической характеристикой, представленной на рисунке 11, то подставляя значение для двух участков, получим систему:

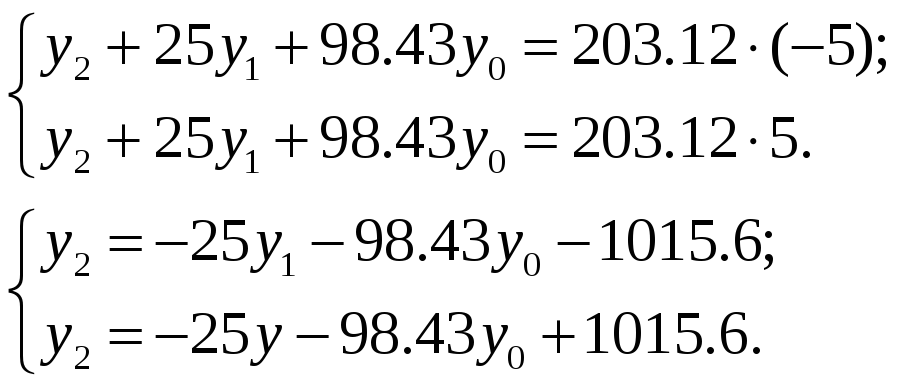
Создадим матрицу для решения дифференциального уравнения.

В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицы для трех начальных условий:

Возьмем количество точек равным 1000 и конечное время интегрирования 200, то матрица решений запишется как: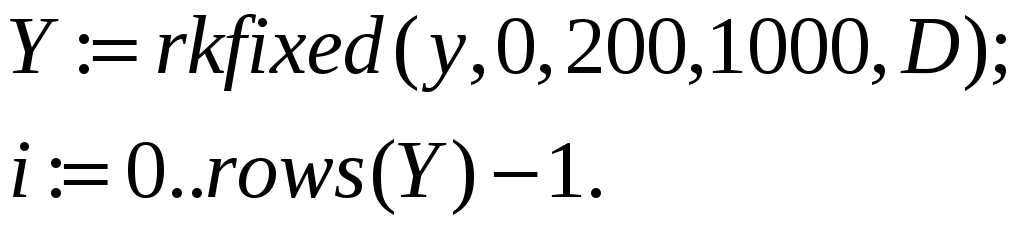

Построим фазовый портрет:

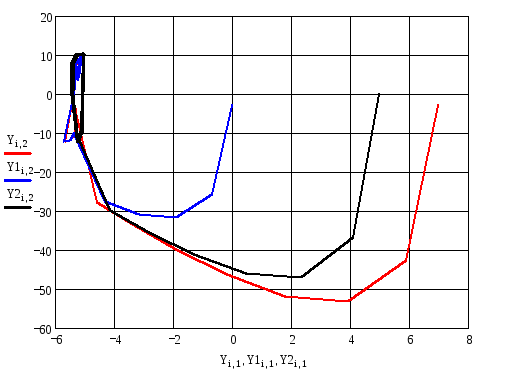
Рисунок 17 - Фазовый портрет нелинейной системы

Рисунок 18 – Переходный процесс

Вывод:

На рисунке 17 представлен фазовый портрет нелинейной системы. Это типовой вид кривой. Переключение с одного уравнения на другое происходит в точке = 5, при >0, и в точке = -5, при <0 . Характер фазовой линии такой, что она стремится к устойчивому состоянию, о чем свидетельствует автоколебательный процесс (рисунок 18), и впоследствии образует замкнутый цикл на фазовом портрете.

Система производит автоколебания в предельном цикле с амплитудой:

, и частотой

Заключение

В ходе данной курсовой работы, была рассмотрена система автоматического регулирования уровня жидкости в гидравлическом резервуаре. Были получены функциональная и структурная схемы системы. Исследована линейная, нелинейная и импульсная части системы.

В ходе исследования линейной части системы, была получена передаточная функция

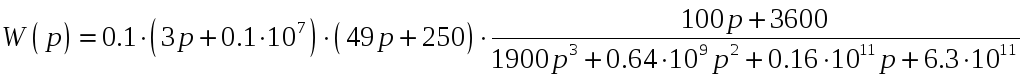, по которой был построен переходный процесс, который свидетельствовал об устойчивости линейной части системы ,и определены прямые оценки качества системы:

- установившееся состояние переходного процесса h_уст=1,4;

- 5% трубка;

- h_max=1.4;

- Время первого согласования t₁=0.25c;

- Время нарастания t_н=0.25c;

- Время регулирования t_р=0.125 c.

Бала построена амплитудо - частотная характеристика системы и определены косвенные оценки качества:

- Амплитуда при нулевой частоте A(0)=1.428;

- Максимальная амплитуда А_max=1.428;

- Резонансная частота w_p=0 Гц;

- Частота среза, при которой амплитуда, равна 1 w_cp=29 Гц;

- Полоса пропускания: w₂=28.16 Гц.

По критериям Гурвица и Найквиста определили, что линейная система устойчива.

В ходе исследования нелинейной части системы, с заданной статической характеристикой нелинейного элемента, был построен фазовый портрет - кривая с замкнутым циклом. Построен переходный процесс нелинейной системы, который свидетельствует об устойчивых автоколебаниях, амплитудой , и частотой . Включение нелинейного элемента в системы никак не отразилось на ее устойчивости.

В ходе исследования импульсной части системы, была получена общая передаточная функция:

.

Провели z –преобразование, и получили:

Построили переходный процесс, по которому можно сказать, что импульсная системы неустойчивая. Критерий Шур Кона показал, что импульсная система неустойчивая. Таким образом при введении импульсного элемента в систему, система становится неустойчивой.