4 Исследование дискретной системы

4.1 Z-преобразование

y(t)

U(t)

Рисунок 15 - Упрощенная схема дискретной системы

Введём вынужденную обратную связь:

y(t)

U(t)

Рисунок 16 - Итоговое преобразование дискретной САУ

Передаточная функция непрерывной части системы:

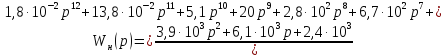
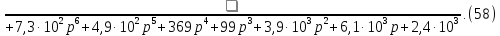
Передаточная функция дискретной части системы:

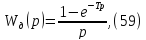
где Т = 0,06 – период дискретизации (шаг квантования)

Примем обозначение е^-Тр=z, получим:

Находим изображение переходной характеристики

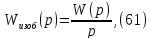
и разлагаем ее на простые дроби:

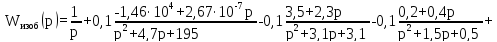
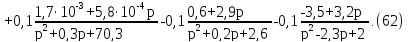
Находим обратное преобразование Лапласа:

Из временной функции получим импульсную и найдем Z-преобразование.

Введём замену t=n·T:

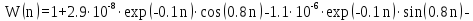
где Т = 0,06 – период дискретизации (шаг квантования).

Z-преобразованная передаточная функция непрерывной части будет иметь вид:

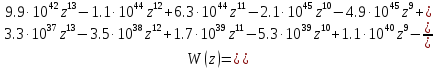
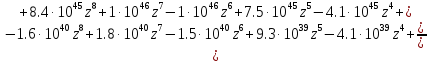
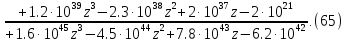
Заменим дискретную часть Z-преобразованной и получим передаточную функцию дискретной системы:

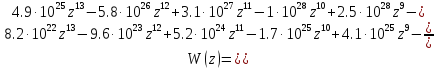
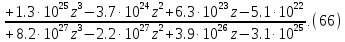
4.2 Устойчивость по критерию Шур-Кона

Определим устойчивость системы по критерию Шур-Кона с помощью Matchad.

В соответствии с критерием Шур-Кона система будет устойчивой, если определители 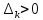для чётных k и определители 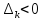для нечётных k.

Определители Шур-Кона составляются из коэффициентов характеристического уравнения.

Характеристическое уравнение системы имеет вид:

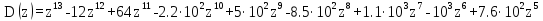
Выпишем коэффициенты характеристического уравнения:

a₁=-12, a₂=64, a₃=-2.2, a₄=5·10², a₅=-8.5·10², a₆=1.1·10³, a₇=-10³, a₈=7.6·10²,

a₉=-4.2·10², a₁₀=1.7·10², a₁₁=-46, a₁₂=7.9, a₁₃=-0.6.

Составим определители:

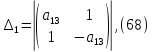
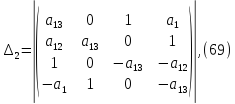
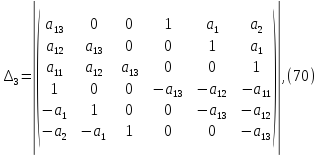
Посчитаем данные определители с помощью Matchad:

∆₁=-0.64,

∆₂=-0.08,

∆₃=0.064,

∆₄=1395.

Видно что при чётных k - 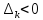, а при нечётных k - 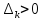, следовательно, система не устойчива.

4.3 Переходный процесс дискретной системы

Используя математический редактор MathCAD, построим переходный процесс системы:

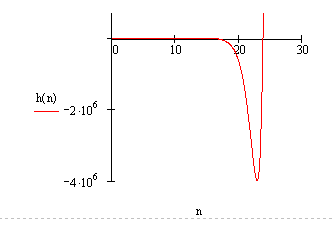
h(n)=8.73*10^-5j(2.87-0.631j)ⁿ+1.15*10^-4(1+1.43*10^-17j)ⁿ-1.64*10^-4(0.788-.394j)ⁿ (72)

h(n)

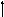
n

Рисунок 17- График переходного процесса дискретной системы

4.4 Билинейное преобразование

Билинейное преобразование отображает внутренность единичного круга на плоскости z в левую полуплоскость плоскости w. Для перехода к нему выполним подстановку:

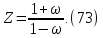
После подстановки передаточная функция имеет следующий вид:

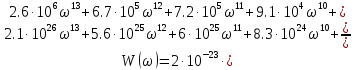
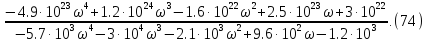
4.5 Построение ЛАЧХ

Произведём λ-преобразование полученной функции. Для этого произведём подстановку:

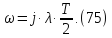
Передаточная функция будет иметь следующий вид:

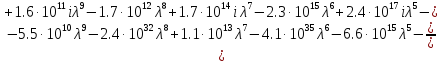
Запишем формулу для построения ЛАЧХ в Matchad:

D(λ)=20·log(A(λ)), (77)

где A(λ)=|W(λ)|. (78)

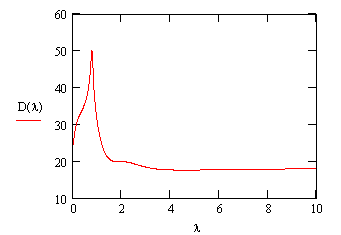
Рисунок 18 – ЛАЧХ непрерывно-дискретной системы.

Запишем формулу для построения ЛФЧХ в Matchad:

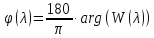. (79)

Рисунок 19 – ЛФЧХ непрерывно-дискретной системы.

4.6 Вывод по исследованию дискретной системы

Для исследования дискретной системы использовалась передаточная функция устойчивой линейной системы. В ходе расчетов выяснилось, что полученная дискретная система является неустойчивой. При помощи математического редактора MATHCAD построили ЛАЧХ и ЛФЧХ системы, по которым невозможно определить запасы устойчивости.

ЗАКЛЮЧЕНИЕ

В ходе данной курсовой работы, была рассмотрена механизированная поточная линия производства обыкновенной шоколадной массы большой производительности. По принципиальной схеме были получены функциональная и структурная схемы системы. Исследована линейная, нелинейная и дискретная части системы.

В ходе исследования линейной системы, была получена передаточная функция, которая проверялась на устойчивость по критерию Гурвица и Михайлова, выяснилось, что система неустойчива. В результате подбора коэффициентов передаточной функции по критерию Евсюкова, система была приведена к устойчивому состоянию. Но по графику переходного процесса видно, что система находится на границе устойчивости.

Далее исследовалось влияние нелинейного элемента на устойчивую линейную систему. В ходе исследования полученной нелинейной системы был построен фазовый портрет, по которому можно судить о том, что нелинейная система устойчива. Следовательно, введение нелинейного элемента в систему не оказало влияние на устойчивость.

В последней части курсовой работы исследовалась дискретная система. В ходе исследования система проверялась на устойчивость по критерию Шур – Кона. В результате проверки выяснилось, что система не устойчива. Следовательно, дискретный элемент оказал отрицательное влияние на устойчивость линейной системы из-за неверного выбора шага дискретизации.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Айзерман М.А. Теория автоматического регулирования. 2- е издание./ Айзерман М.А. – М.: Наука,1966. – 452 с.

2. Бесекерский В.А. Теория систем автоматического регулирования/ В.А. Бесекерский, Е.П. Попов. – М.: Профессия, 2003. – 380 с.

3. Климовицкий М.Д. Автоматический контроль и регулирование: Справочник. – Л.: Металлургия, 1987. – 345 с.

4. Кошарский Б.Д., Автоматические приборы и регуляторы./ Кошарский Б.Д.– М.: Машиностроение, 1964. – 704 с.

5. Летов А.М. Устойчивость нелинейных регулируемых систем./ Летов А.М. – М.: Физматгиз, 1962. – 315 с.

6. Поспелов Г.С. Импульсные системы автоматического регулирования. – М.: Машгиз, 1950. – 256 с.

7. Пугачев В.С.Основы автоматического регулирования. – М.: Наука, 1974. –720 с.

8. Топчеев Ю.И. Атлас для проектирования систем автоматического управления. – М.: Машиностроение, 1982. – 312 с.