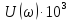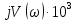- •4.5 Лачх системы и определение запасов устойчивости 26
- •1.2 Функциональная схема сау
- •1.3 Структурная схема сау
- •2 Исследование линейной сау
- •2.1 Расчет передаточной функции
- •2.2 Определение устойчивости сау по критерию Гурвица
- •2.3 Определение устойчивости сау по критерию Михайлова
- •2.4 Определение устойчивости сау по критерию Евсюкова
- •3 Исследование нелинейных систем
- •3.1 Преобразование системы
- •3.2 Построение фазового портрета
- •3.3 Вывод по исследованию нелинейной системы
- •4 Исследование дискретной системы
- •4.6 Вывод по исследованию дискретной системы
- •Битту уит – 42
- •Пояснительная записка
2 Исследование линейной сау
2.1 Расчет передаточной функции
Передаточная функция системы рассчитывается по формуле:

Для расчетов используем программу Mathcad.

2.2 Определение устойчивости сау по критерию Гурвица
Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительны. По коэффициентам характеристического уравнения составляется определитель Гурвица.
L(p)= (3)
(3)
Составим определитель Гурвица

Произведем вычисление миноров в определителе Гурвица
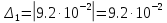 ,
(4)
,
(4)
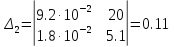 ,
(5)
,
(5)
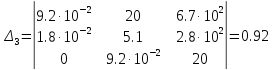 ,
(6)
,
(6)
 ,
(7)
,
(7)

 ,
(8)
,
(8)

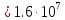 ,
(9)
,
(9)
 (10)
(10)
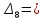

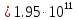 ,
(11)
,
(11)


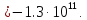 (12)
(12)
Система не устойчива, т.к. диагональный минор Δ9 отрицательный.
2.3 Определение устойчивости сау по критерию Михайлова
Для устойчивой системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности повернулся против часовой стрелки, начиная с вещественной оси, на число квадрантов равное порядку характеристического уравнения (3), последовательно проходя эти квадранты.
Заменим
в уравнении (3)
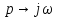 :
:
L(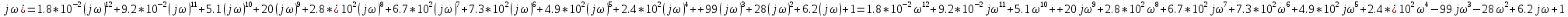 .
(13)
.
(13)
Выделим вещественную и мнимую части:

Таблица
2-Значения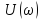 и
и
 при изменении
при изменении
 от 0 до 1.2
от 0 до 1.2
|
№ |
|
|
|
|
1 |
0 |
1 |
0 |
|
2 |
0.2 |
0.311 |
0.613 |
|
3 |
0.4 |
5.838 |
2.265 |
|
4 |
0.6 |
60.817 |
39.396 |
|
5 |
0.8 |
320.274 |
258.037 |
|
6 |
1 |
1.228*103 |
1.087*103 |
|
7 |
1.2 |
3.874*103 |
3.56*103 |
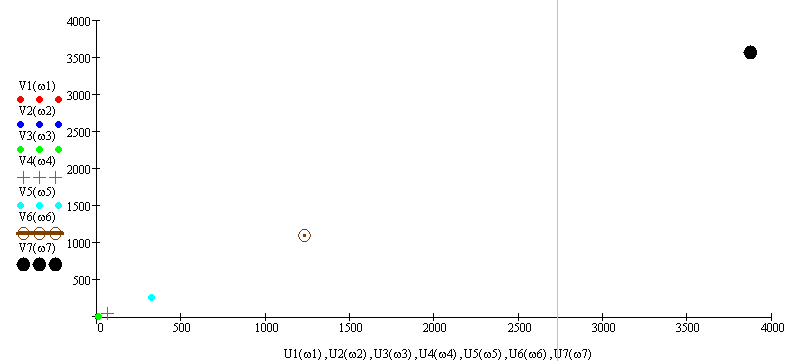
U(ω)
(W
V(ω)
(W



Рисунок 4 - Годограф Михайлова
Система не устойчива, так как вектор не обходит последовательно n-квадрантов.
2.4 Определение устойчивости сау по критерию Евсюкова
Определим величины k:
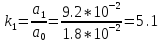 ,
(15)
,
(15)
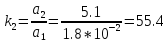 ,
(16)
,
(16)
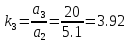 ,
(17)
,
(17)
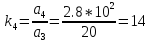 ,
(18)
,
(18)
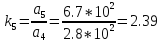 ,
(19)
,
(19)
 ,
(20)
,
(20)
 ,
(21)
,
(21)
 ,
(22)
,
(22)
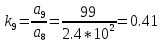 ,
(23)
,
(23)
 ,
(24)
,
(24)
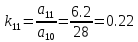 ,
(25)
,
(25)
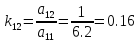 .
(26)
.
(26)
Определим величины n:
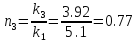 ,
(27)
,
(27)
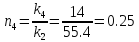 ,
(28)
,
(28)
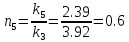 ,
(29)
,
(29)
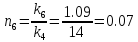 ,
(30)
,
(30)
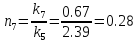 ,
(31)
,
(31)
 ,
(32)
,
(32)
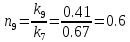 ,
(33)
,
(33)
 ,
(34)
,
(34)
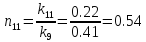 ,
(35)
,
(35)
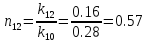 ,
(36)
,
(36)

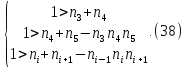
Условия (38) не выполняются, следовательно, система не устойчива. Приведем систему к устойчивому состоянию. Для этого уменьшим коэффициенты n3, n9, n10, n12 в 1,5 раза и получим значение n3 = 0.51, n9=0.4, n10 =0.38, n12 =0.38. Условие (38) выполняется, система устойчива.
Для получения устойчивой системы коэффициенты n3, n9, n10, n12 были уменьшены в 1,5 раза, значит необходимо увеличить коэффициент k1 , k9 , k10 , k12 в 1,5 раза, согласно формулам (27),(33)-(34),(36). Тогда k1=7.68, k9=0.268, k10 =0.186, k12=0.07. Для того, чтобы система стала устойчивой необходимо в характеристическом уравнении изменить значение коэффициентов а1, а8, а10, а11, которые согласно формулам (15), (23)-(24), (26) примут следующие значения:
а1=13,82*10-2, а8=369, а10=18.4, а11=14,3.
Передаточная функция САУ примет вид:

2.5 Переходный процесс системы и определение показателей качества
Используя математический редактор MathCAD, построим переходный процесс системы.
h(t)=2.37*103+2.94*10-8exp(-2.36t)cos(13.8t)-1.18*106exp(-2.36t)*
*sin(13.8t) (40)
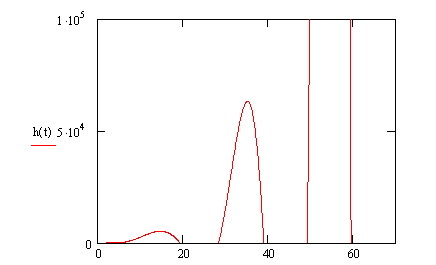

Рисунок 5 - Переходный процесс системы
2.6 АЧХ системы и определение показателей качества
Используя математический редактор MathCAD, построим амплитудно-частотную характеристику системы.
Заменим
в уравнении (39)
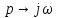 :
:
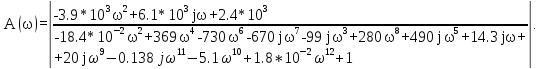 (41)
(41)
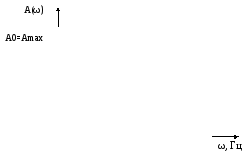

Рисунок 6 - Амплитудно–частотная характеристика системы
Определение показателей качества:
А0 = 2400;
Аmax = 2400;
показатель
колебательности
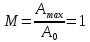 ;
;
полоса
пропускания
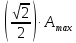 =
1697
=
1697
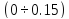 .
.
2.7 ЛАЧХ системы и определение запасов устойчивости
Используя математический редактор MATLAB, построим ЛАЧХ и ЛФЧХ системы.
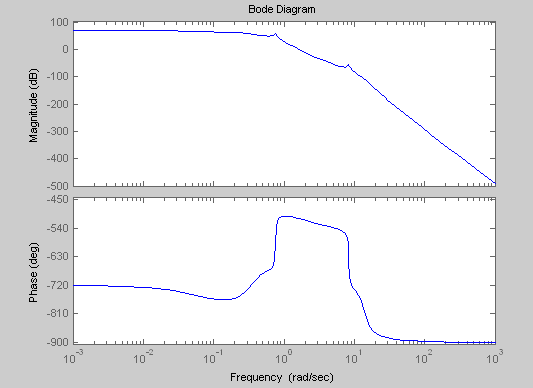
φ(ω)
L(ω)
(W
ω, Гц

Рисунок 7 - ЛАЧХ системы
2.8 Аппроксимация ЛАЧХ и определение передаточной функции
L(ω)
(W

φ(ω)

ω, Гц

Рисунок 8-Аппроксимация ЛАЧХ системы
Передаточная функция аппроксимированной ЛАЧХ имеет вид:
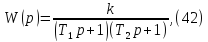
 ,
(43)
,
(43)
 .
(44)
.
(44)
С учетом коэффициентов выражение (42) примет вид:
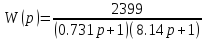 .
(45)
.
(45)
2.9 Вывод по исследованию линейной системы
В ходе исследования линейной системы была получена передаточная функция системы. Определили, что система является неустойчивой по критериям устойчивости Гурвица, Михайлова и Евсюкова. Благодаря критерию устойчивости Евсюкова система была приведена к устойчивому состоянию. Построили переходный процесс и АЧХ системы, определили показатели качества. При помощи математического редактора MATLAB построили ЛАЧХ системы и определили запасы устойчивости.