Получим передаточную функцию замкнутой системы по возмущающему воздействию:

В качестве канала возбуждения используем аппроксимирующую передаточную функцию первого порядка:

.

Преобразуем схему:

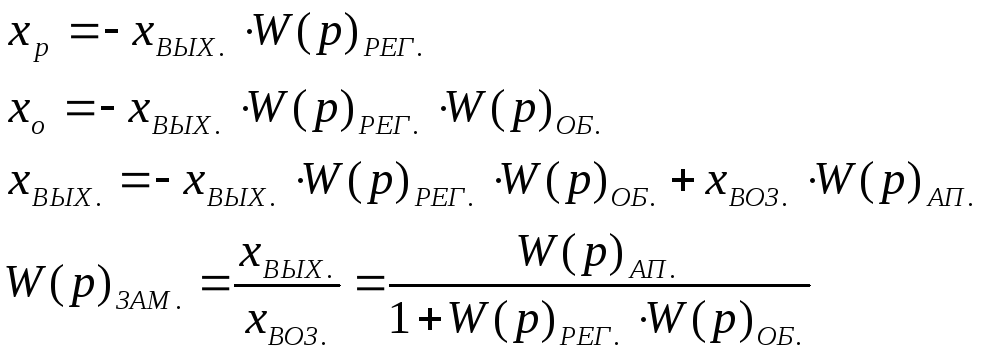
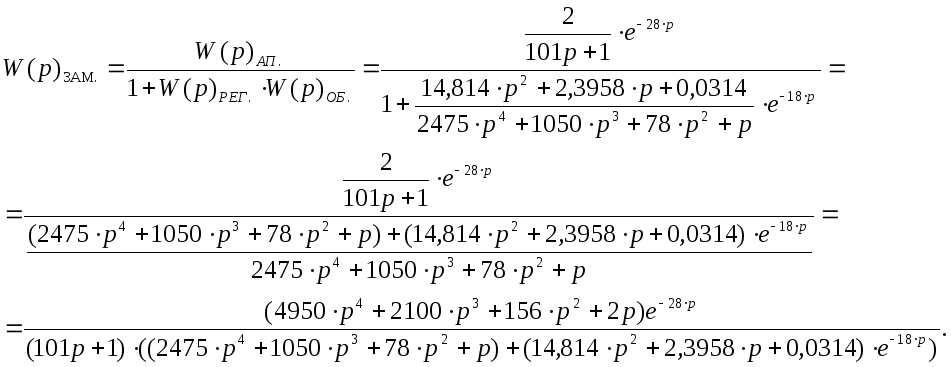
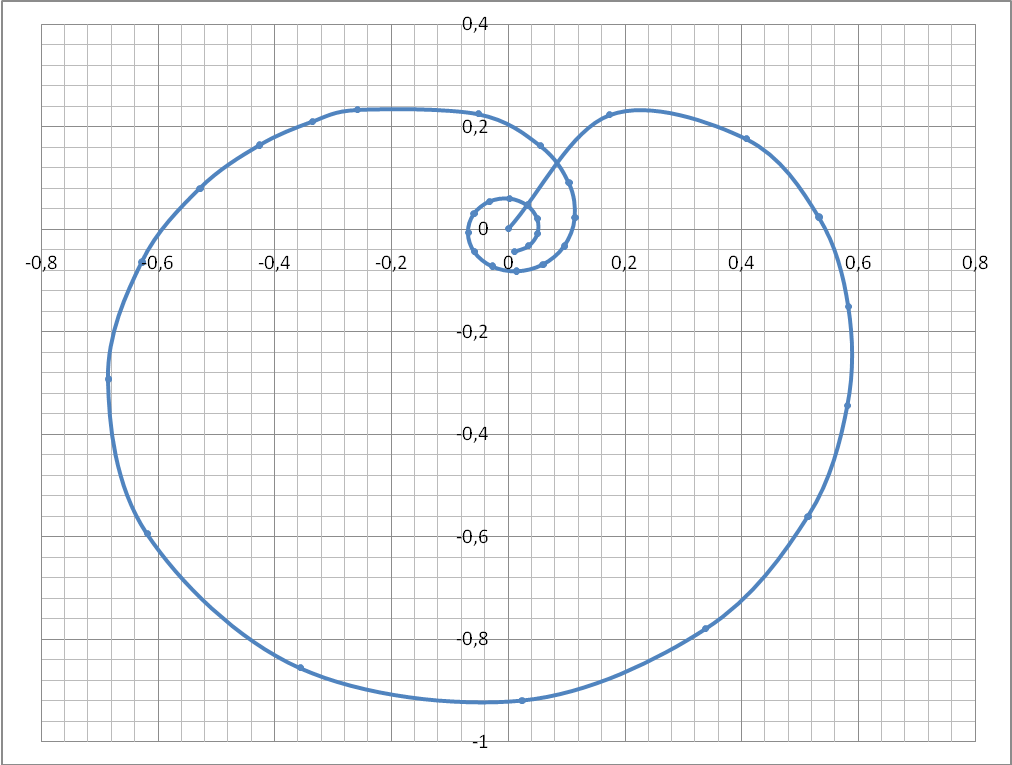
Рассчитаем и построим АФХ замкнутой системы по возмущению:

0	0	0
0,005	0,1739	0,2225
0,01	0,4077	0,1759
0,015	0,5323	0,0231
0,02	0,5828	-0,1516
0,025	0,5812	-0,3442
0,03	0,5134	-0,5604
0,035	0,3381	-0,78
0,04	0,0232	-0,9197
0,045	-0,3569	-0,8563
0,05	-0,6191	-0,5939
0,055	-0,6854	-0,2929
0,06	-0,6281	-0,0647
0,065	-0,5286	0,0793
0,07	-0,42689	0,1634
0,075	-0,3361	0,2096
0,08	-0,2585	0,2326
0,1	-0,0517	0,2244
0,12	0,0547	0,1628
0,14	0,104	0,0903
0,16	0,114	0,0219
0,18	0,0958	-0,0333
0,2	0,0592	-0,0691
0,22	0,0144	-0,0821
0,24	-0,0278	-0,0725
0,26	-0,0579	-0,0446
0,28	-0,069	-0,0068
0,3	-0,059	0,0296
0,32	-0,0321	0,0541
0,34	0,0023	0,0598
0,36	0,0327	0,0464
0,38	0,0499	0,02
0,4	0,05	-0,0096
0,42	0,0348	-0,0331
0,44	0,011	-0,0441
0,46	-0,0133	-0,0409
0,48	-0,0314	-0,0262
0,5	-0,0386	-0,0055
0,51	-0,0378	0,0051
0,52	-0,0342	0,015
0,53	-0,0283	0,0233
0,54	-0,0204	0,0296
0,55	-0,0113	0,0335
0,56	-0,0017	0,0347
0,57	0,0077	0,0333
0,58	0,0163	0,0294
0,59	0,0234	0,0234
0,6	0,0286	0,0159
0,61	0,0314	0,0072
0,62	0,0317	-0,0016
0,63	0,0296	-0,0102
0,64	0,0253	-0,0178
0,65	0,0191	-0,0238
0,66	0,0116	-0,0278
0,67	0,0033	-0,0295
0,68	-0,0049	-0,0289
0,69	-0,0126	-0,026
0,7	-0,0191	-0,0212

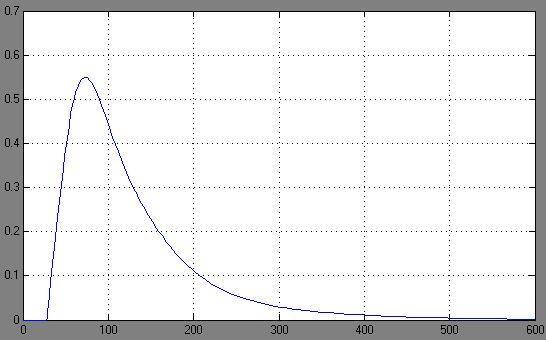
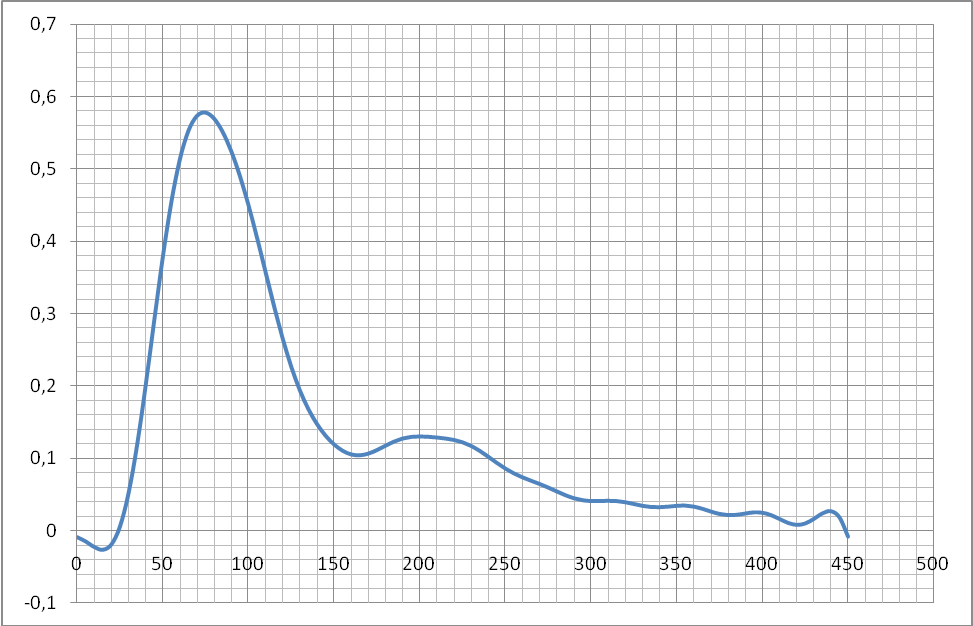
• Построим переходной процесс в системе регулирования при единичном скачкообразном возмущающем воздействии методом Акульшина:

Переходной процесс при единичном возмущающем воздействии: ,

Т- период скачкообразного возмущающего воздействия, амплитуда возмущения.

= выражение для расчета переходного процесса.

Преобразуем выражение под знаком суммы:

Перейдем к вещественной и мнимой частотным характеристикам:

=;, получим

=.Подставим в исходное выражение, получим:

; амплитуда возмущающего воздействия;; , -ВЧХ и МЧХ замкнутой системы по возмущающему воздействию; . Т.к. , то

0	-0,00926
5	-0,01527
10	-0,02298
15	-0,02672
20	-0,01943
25	0,00534
30	0,05133
35	0,11803
40	0,20051
45	0,29042
50	0,378
55	0,45446
60	0,51372
65	0,55329
70	0,57388
75	0,57825
80	0,56978
85	0,55129
90	0,52459
95	0,49069
100	0,45045
105	0,40529
110	0,35748
115	0,3099
120	0,26548
125	0,22645
130	0,19393
135	0,16782
140	0,14728
145	0,13123
150	0,11894
155	0,11021
160	0,10519
165	0,10401
170	0,10634
175	0,11125
180	0,11729
185	0,12298
190	0,12719
195	0,12947
200	0,13007
205	0,12959
210	0,12859
215	0,12724
220	0,12522
225	0,12194
230	0,11691
235	0,11007
240	0,10193
245	0,09344
250	0,08554
255	0,07886
260	0,07344
265	0,06879
270	0,06424
275	0,05929
280	0,05396
285	0,04879
290	0,04453
295	0,04182
300	0,04073
305	0,04075
310	0,04098
315	0,04053
320	0,03897
325	0,03657
330	0,0341
335	0,03245
340	0,03213
345	0,03294
350	0,03404
355	0,03431
360	0,03294
365	0,02992
370	0,02609
375	0,0228
380	0,02121
385	0,02169
390	0,02346
395	0,02494
400	0,02445
405	0,02118
410	0,01579
415	0,01039
420	0,0077
425	0,00964
430	0,01599
435	0,02359
440	0,02661
445	0,01796
450	-0,00866

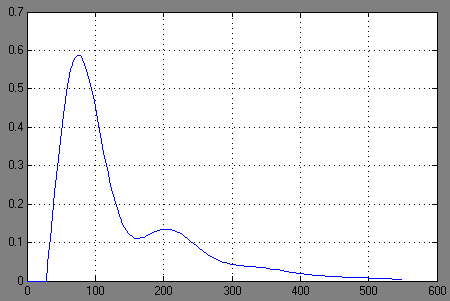
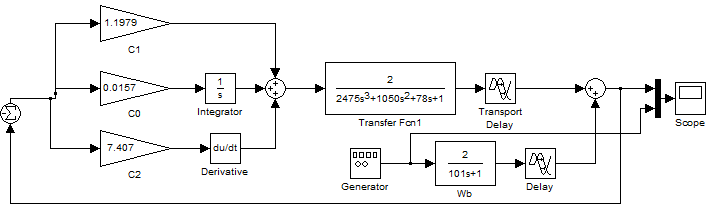
• Построим переходной процесс в системе регулирования при единичном скачкообразном возмущающем воздействии c использованием АЧХ замкнутой системы:

Построим АЧХ замкнутой системы по возмущению:

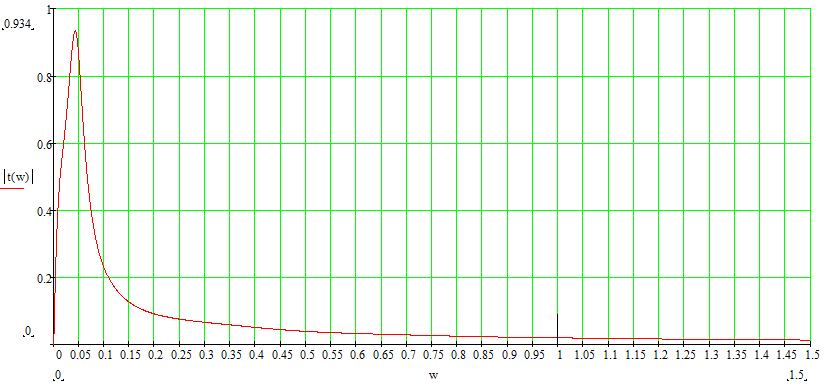
Определим приближенное значение частоты среза .

Используем обратное преобразование Фурье для получения выражения для расчета переходного процесса: 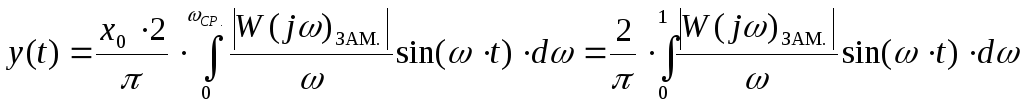,где амплитуда возмущающего воздействия; АФХ замкнутой системы по возмущению.

0	0
10	0,3966
20	0,5949
30	0,6771
35	0,6845
40	0,6746
50	0,6184
60	0,5373
70	0,4521
80	0,3776
90	0,3212
100	0,2843
110	0,2647
120	0,2577
130	0,2579
140	0,2607
150	0,2624
160	0,261
170	0,2559
180	0,2471
190	0,2359
200	0,2234
210	0,2109
220	0,1992
230	0,1889
240	0,1801
250	0,1729
260	0,1669
270	0,1617
280	0,1572
290	0,1529
300	0,1485
340	0,1309
380	0,1154
420	0,1036
460	0,0939
500	0,0858
550	0,0772

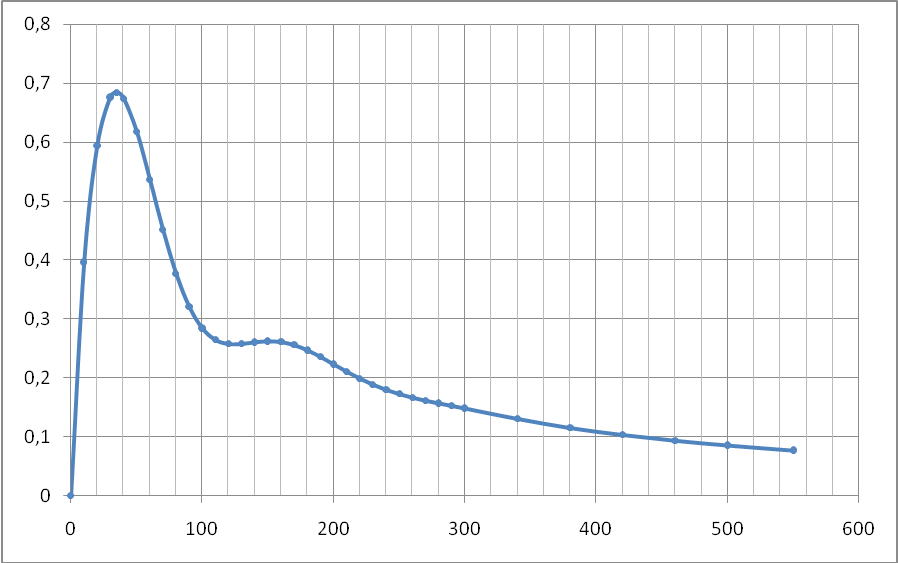
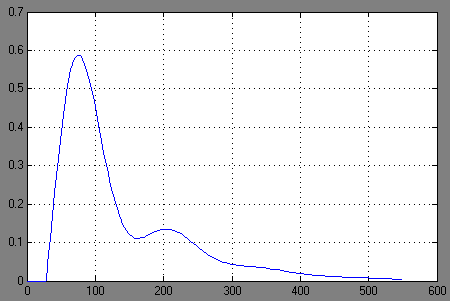
Из расчетных переходных процессов наиболее близким к экспериментальному является процесс построенный методом Акульшина. Процесс полученный через обратное преобразование Фурье отличается от экспериментального отсутствием запаздывания и большей амплитудой первого максимума.

• Оценим качество переходного процесса:

1. Определим время переходного процесса: .

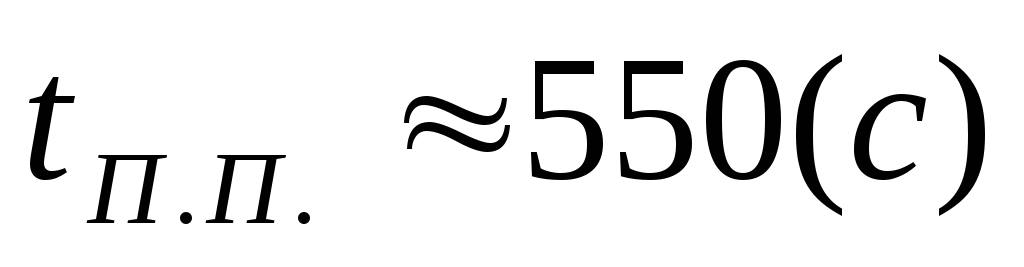2. Определим декремент затухания: .

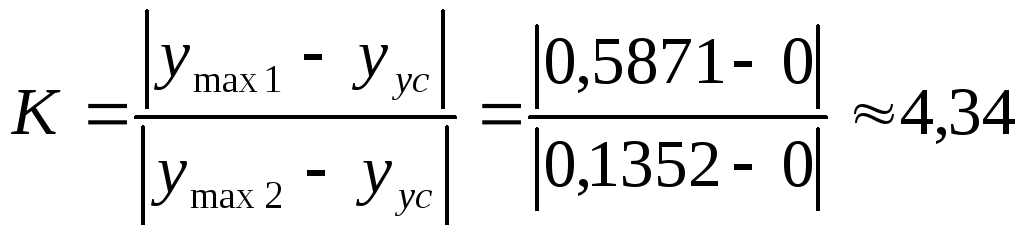3. Определим время установления (достижение первого max):

4. Определим время длительности фронта (время нарастания переходного процесса): .

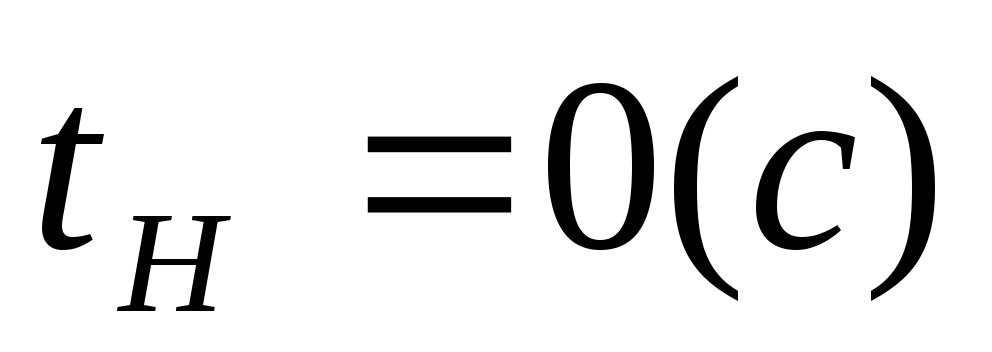5. Определим число колебаний за время переходного процесса: .

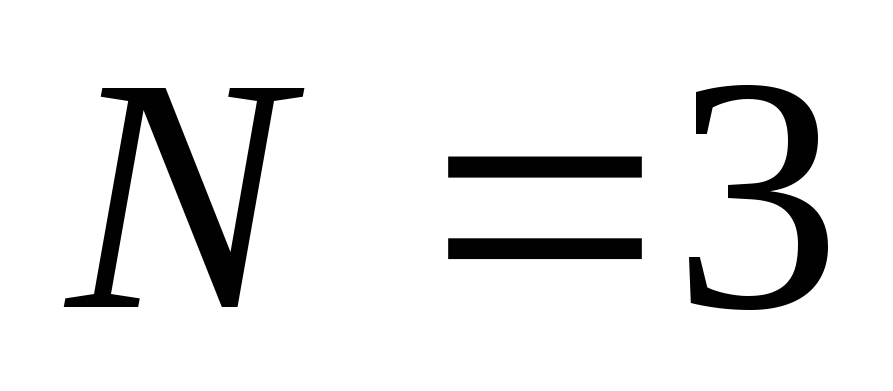6. Определим собственную частоту колебаний системы: 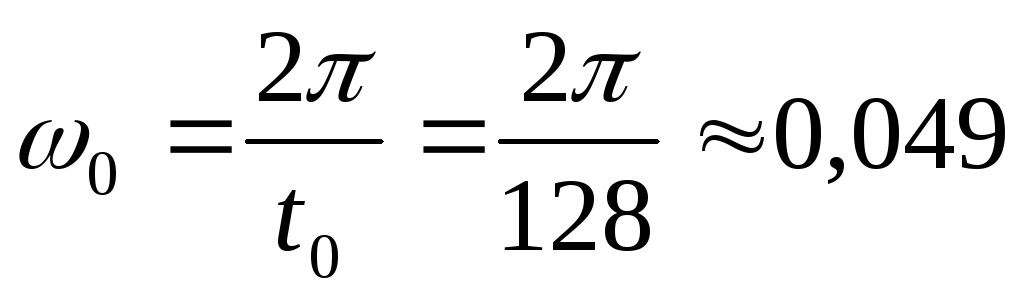(рад/с).

7. Статическая ошибка: .

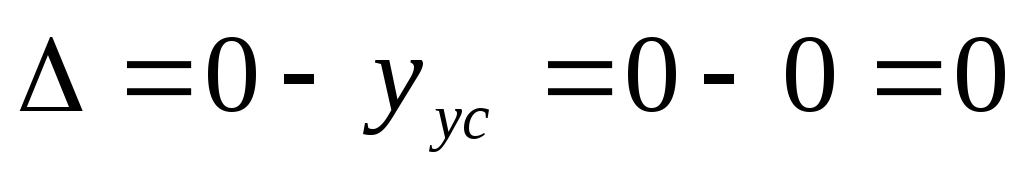8. Определим степень затухания: .

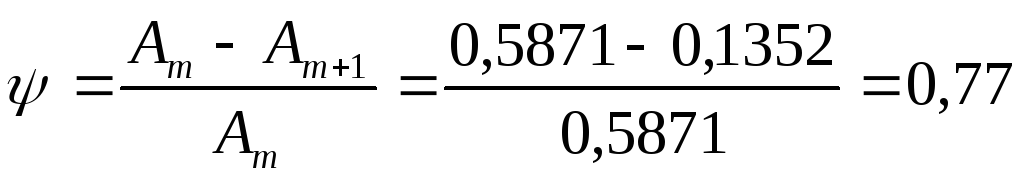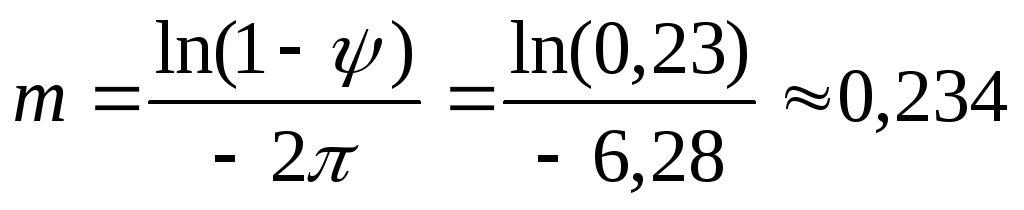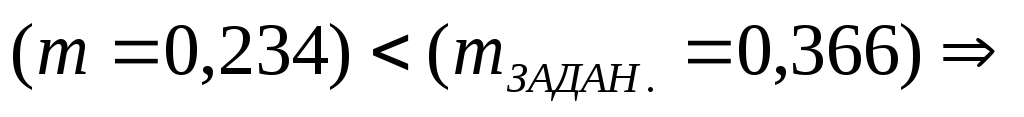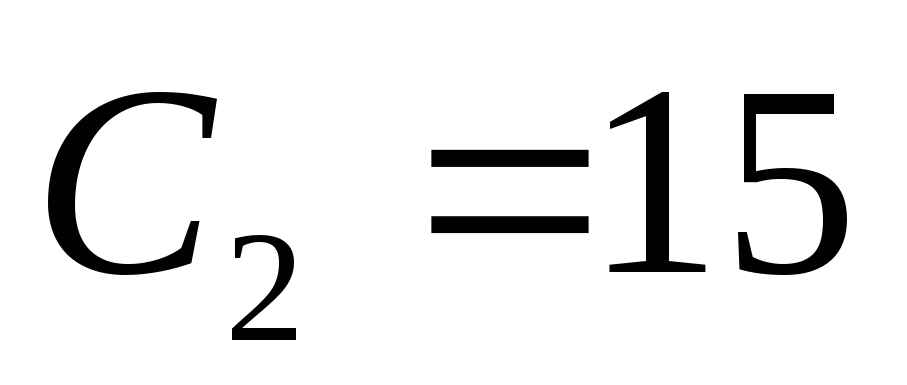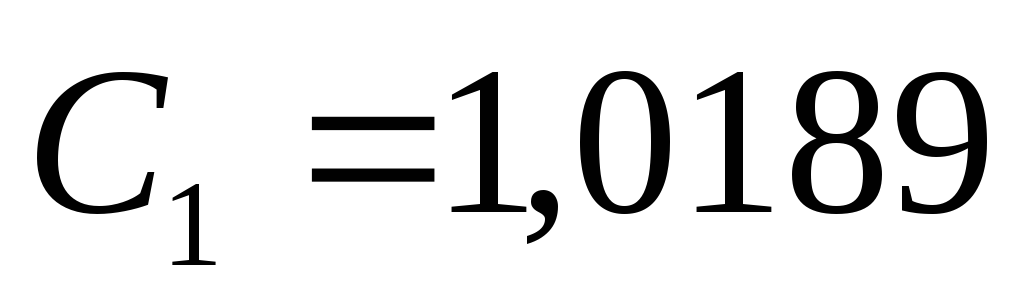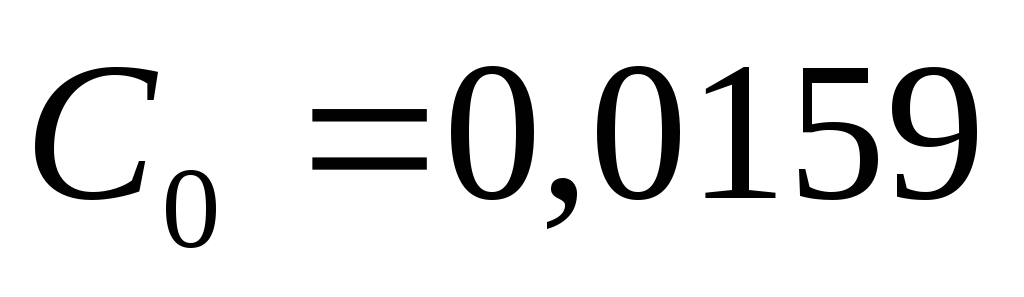9. Определим степень колебательности: . Т.к. необходимо уточнить настройки регулятора с целью достижения заданной степени колебательности. После уточнения получим: ; ; . Интегральный квадратичный критерий качества: .
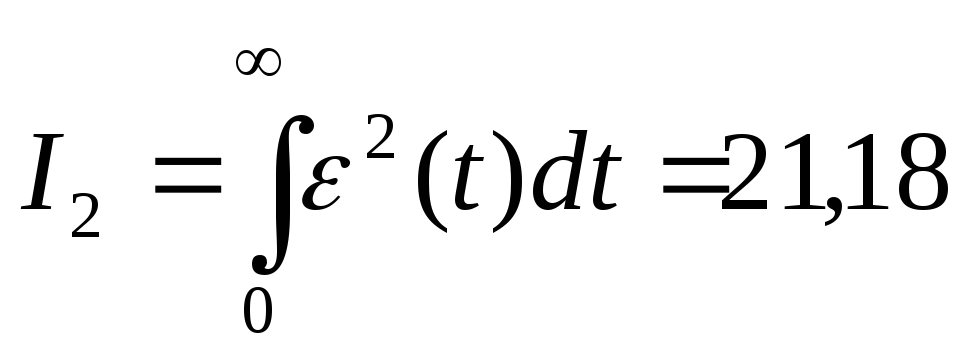