10.1.3. Построение зависимостей ,,при ступенчатом приложении нагрузки

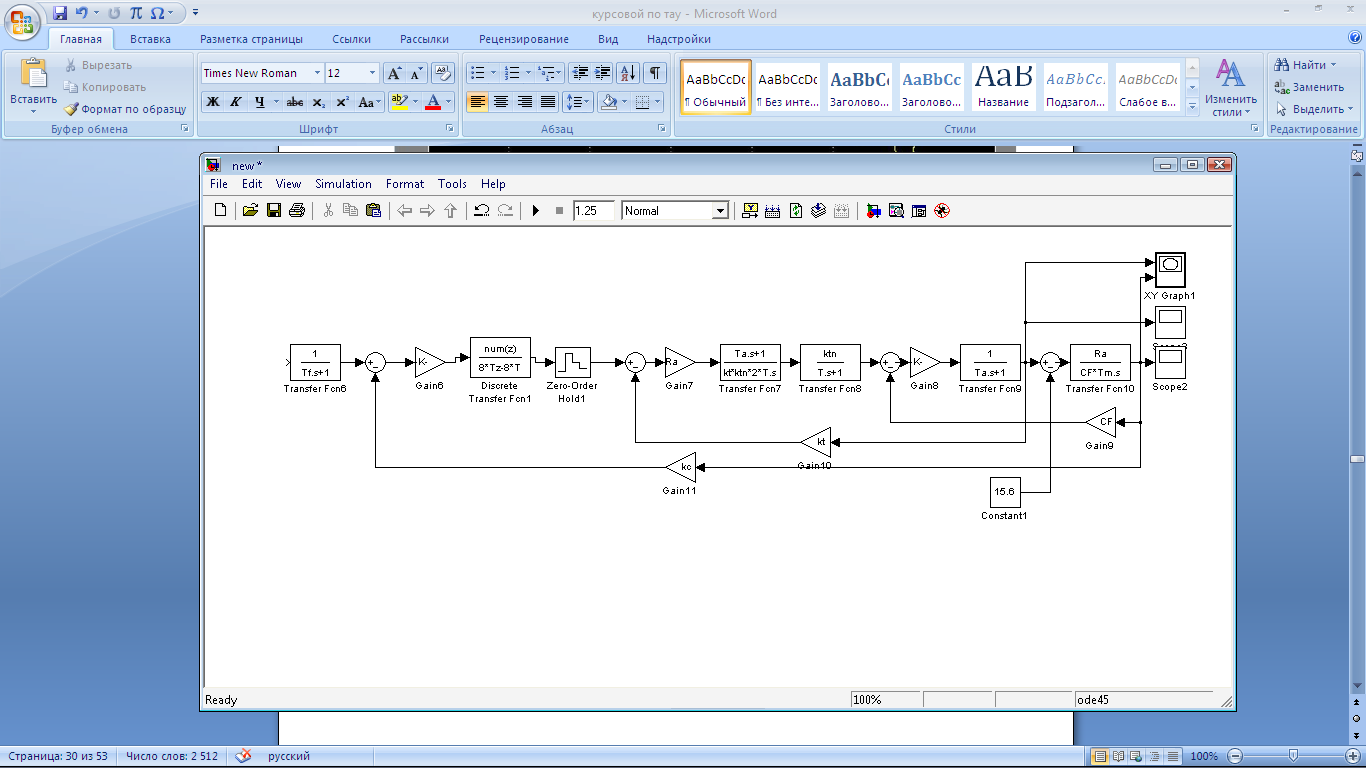
Рис. 33 Структурная схема для построения зависимостей , ,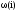с фильтром

T = 0.5*Ta

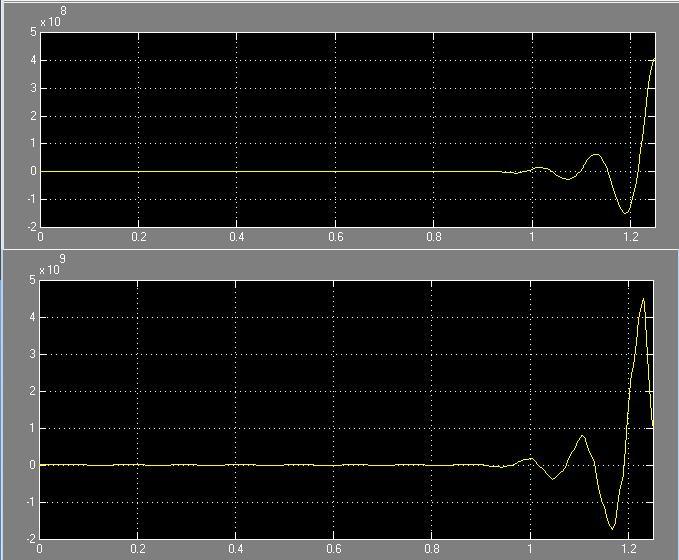
Рис. 34. Зависимость системы w(t) и i(t) с цифровым регулятором с фильтром при ступенчатом приложении нагрузки

T = 0.05*Ta

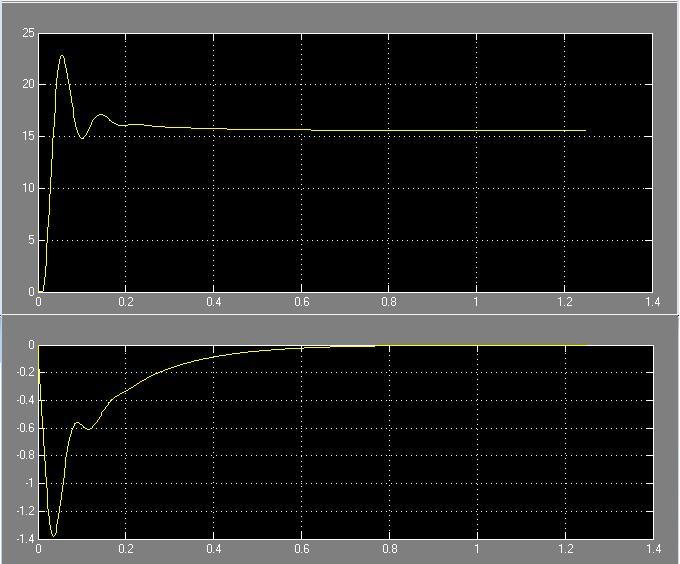
Рис. 35. Зависимость системы i(t) и w(t) с цифровым регулятором с фильтром

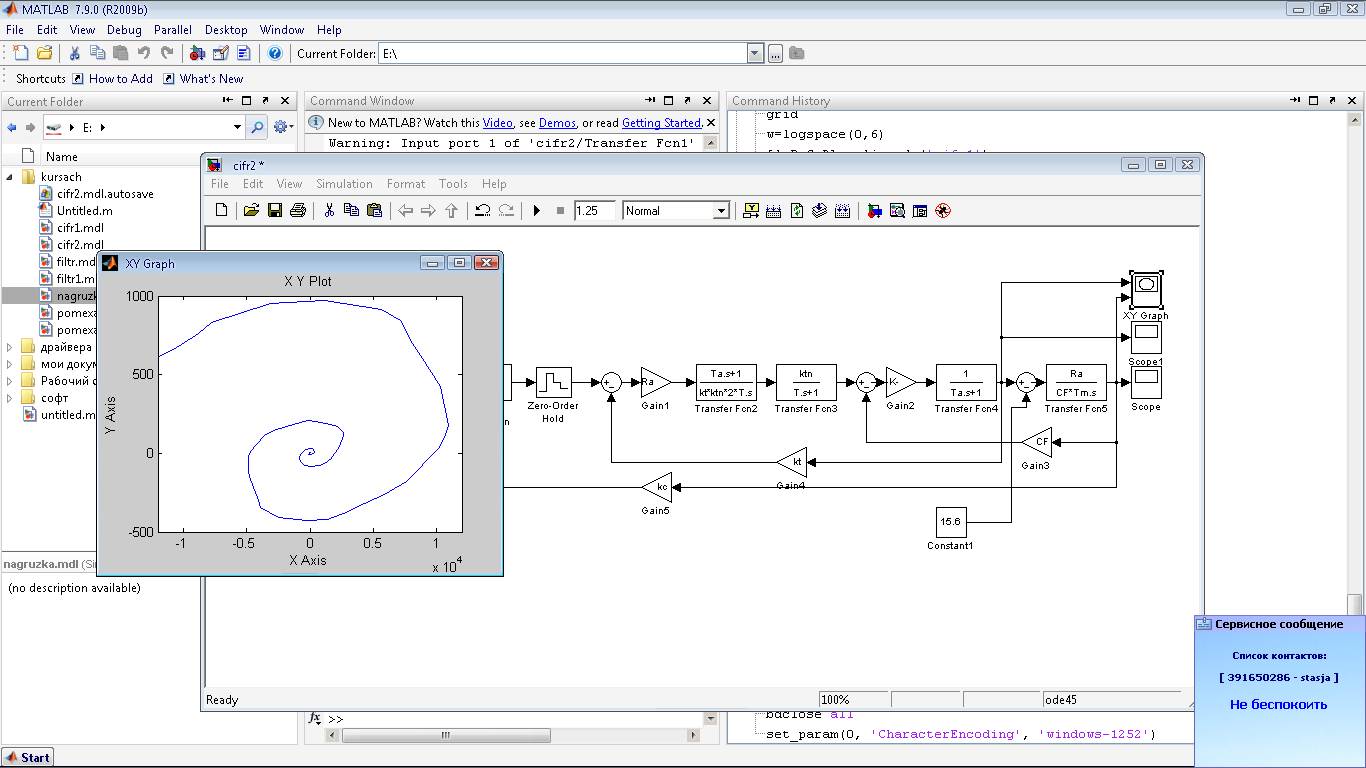
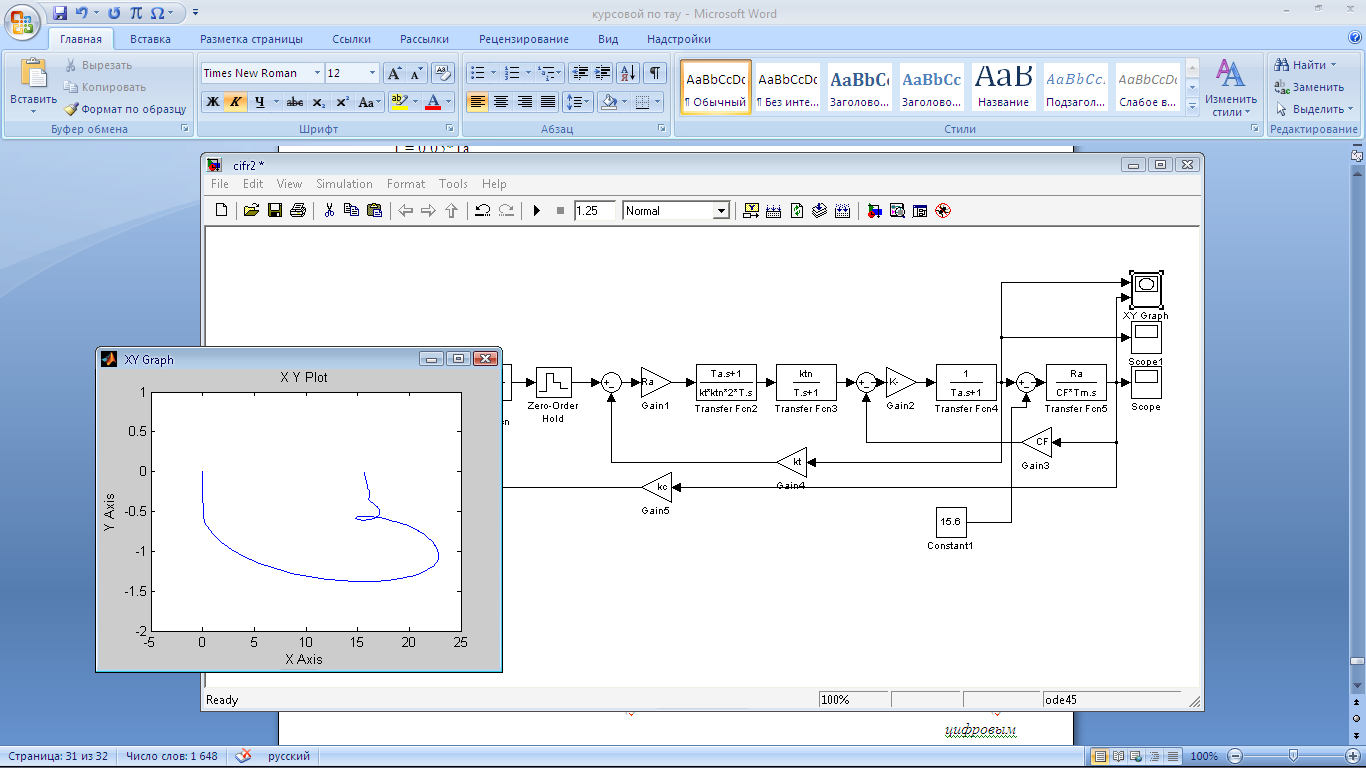
Рис. 36 Зависимость системы с Рис. 37 Зависимость системы с

цифровым регулятором скорости цифровым регулятором скорости

при T = 0.5*Ta с фильтром при T = 0.05*Ta с фильтром

Определение установившейся ошибки

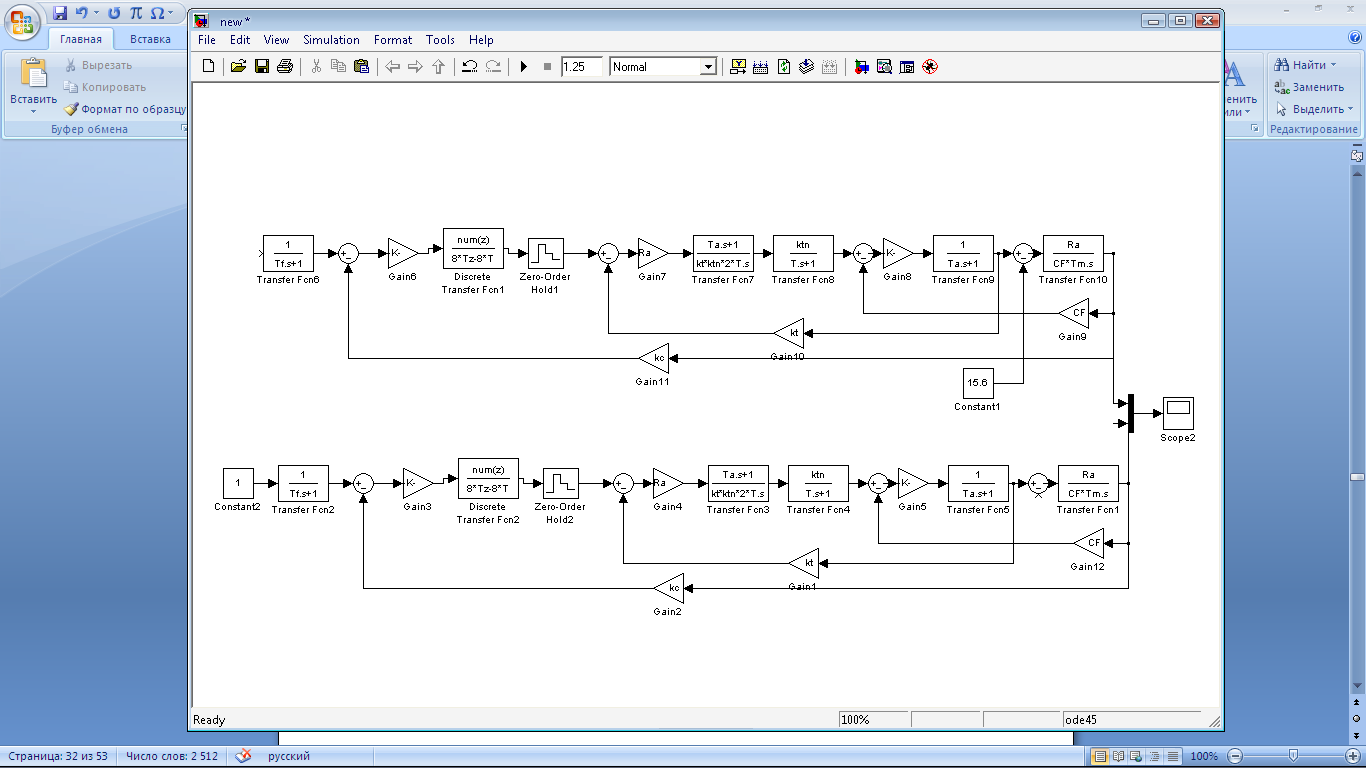
Рис. 37.1 Зависимость системы i(t) и w(t) с цифровым регулятором с фильтром

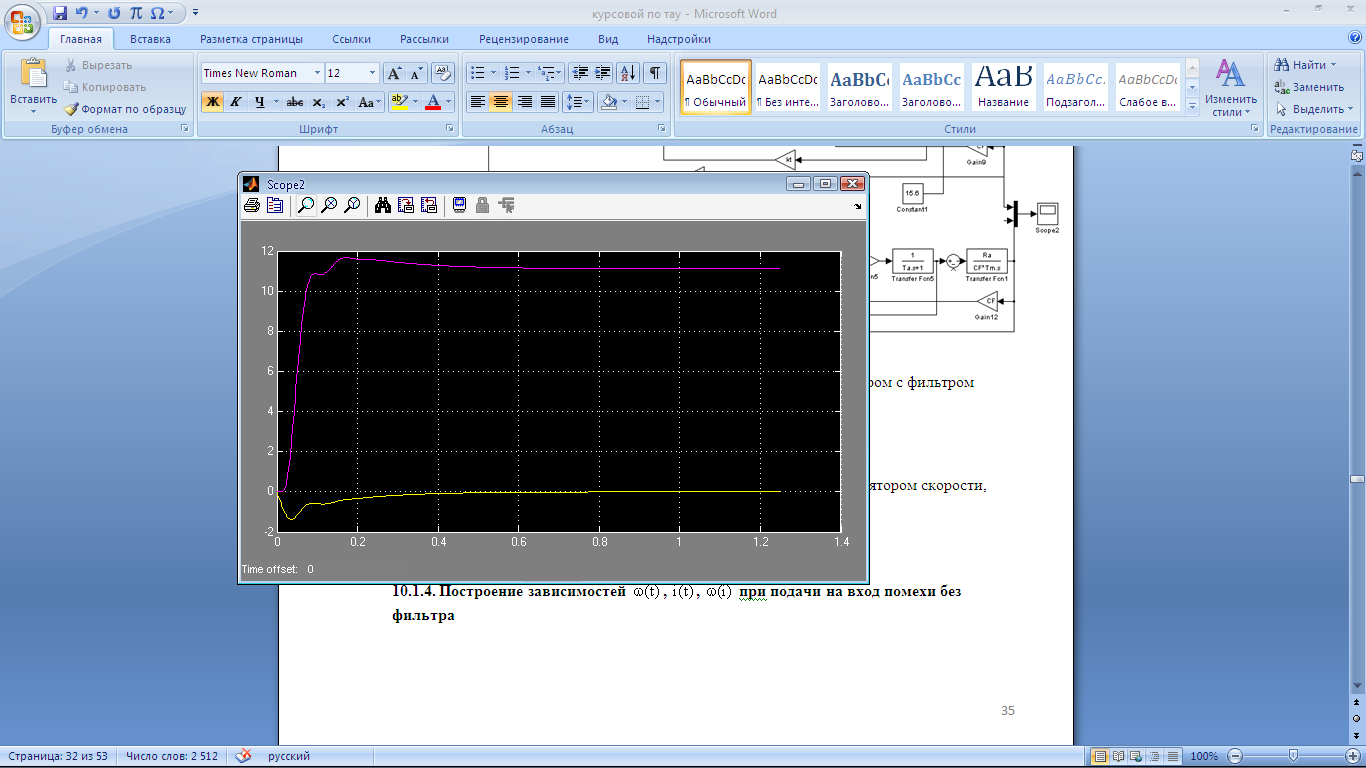
Рис. 37.2 Получившийся процесс

По отношению к сигналу нагрузки, так же как и с не цифровым регулятором скорости, система астатична, следовательно, е_уст = 0.

10.1.4. Построение зависимостей ,,при подачи на вход помехи без фильтра

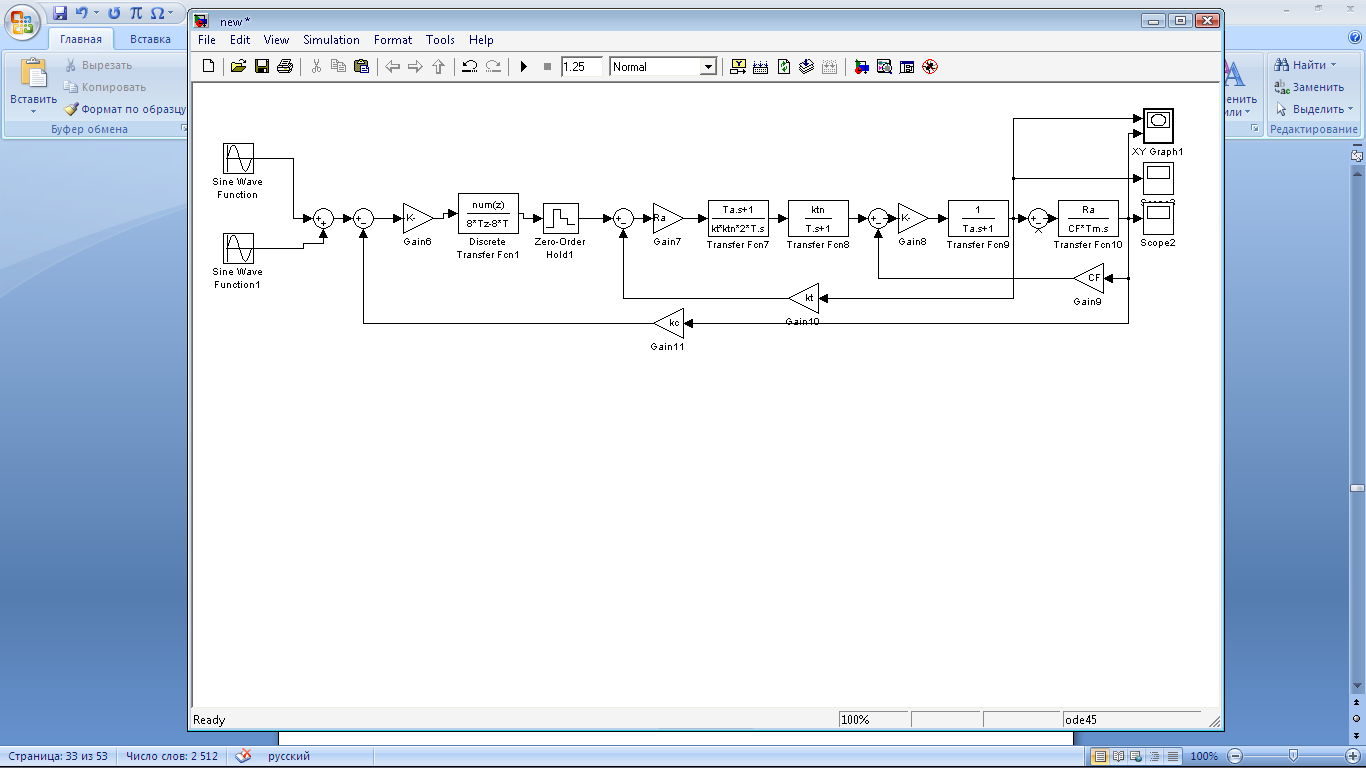
Рис. 38. Структурная схема для построения зависимостей,,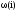без фильтра

T = 0.05*Ta

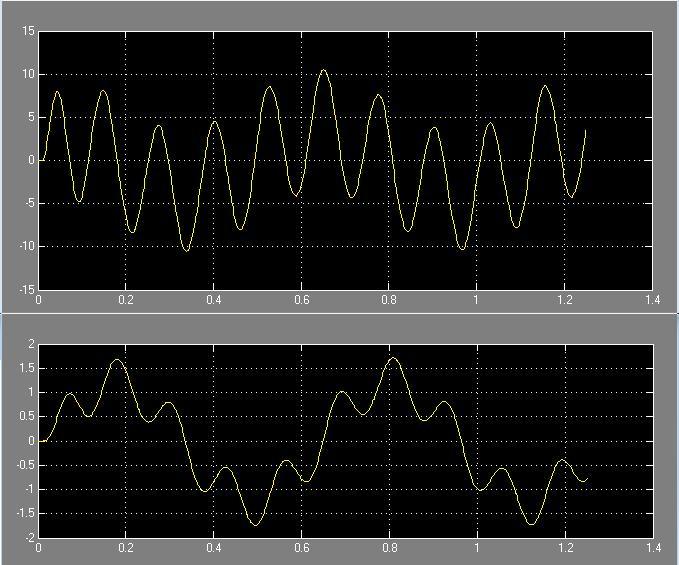
Рис. 39 Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

T = 0.5*Ta

Рис. 40 Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

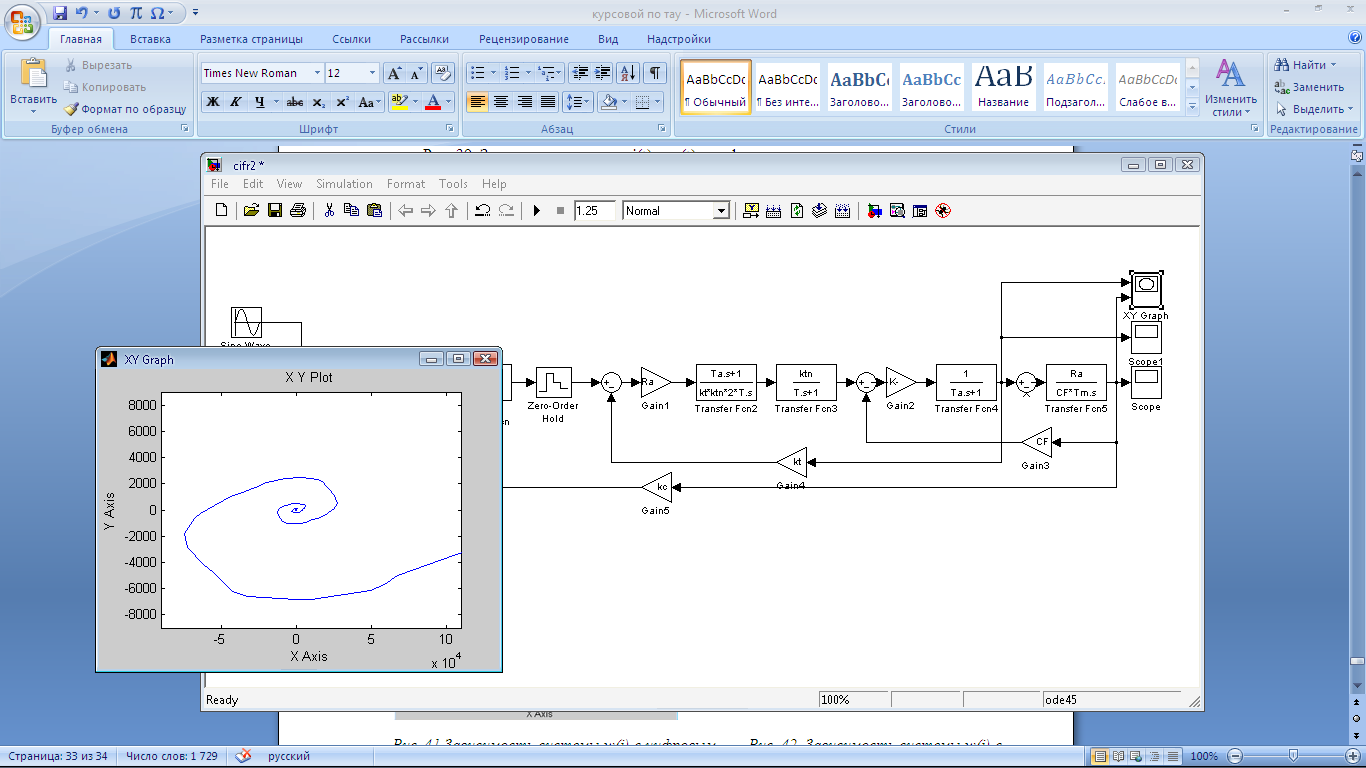
Рис. 41 Зависимость 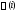системы с Рис.42 Зависимость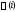системы с

цифровым регулятором скорости цифровым регулятором скорости

при T = 0.05*Ta с фильтром при T = 0.5*Ta с фильтром

10.1.5. Построение зависимостей ,,при подачи на вход помехи с фильтром

Рис. 43 Структурная схема для построения зависимостей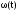,,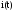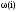с фильтром

T = 0.05*Ta

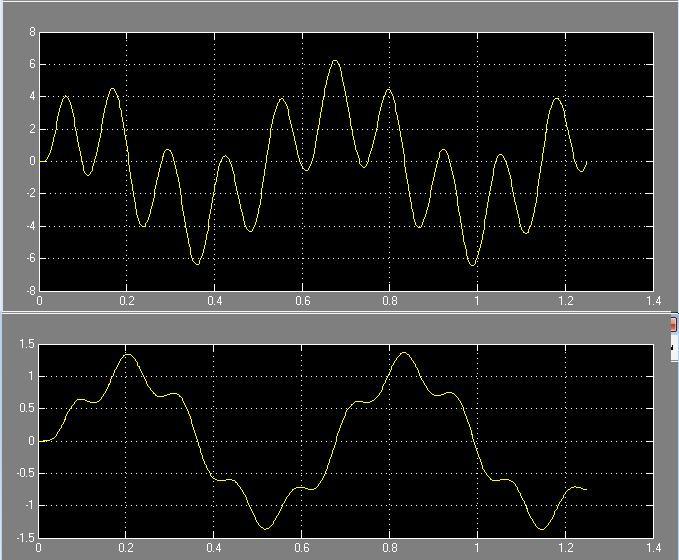
Рис. 44 Зависимость системы i(t) и w(t) с цифровым регулятором с фильтром

T = 0.5*Ta

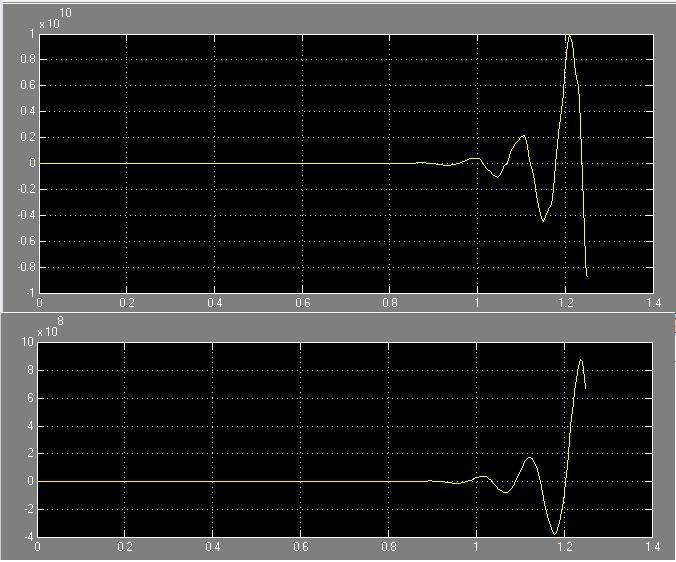
Рис. 45 Зависимость системы i(t) и w(t) с цифровым регулятором с фильтром

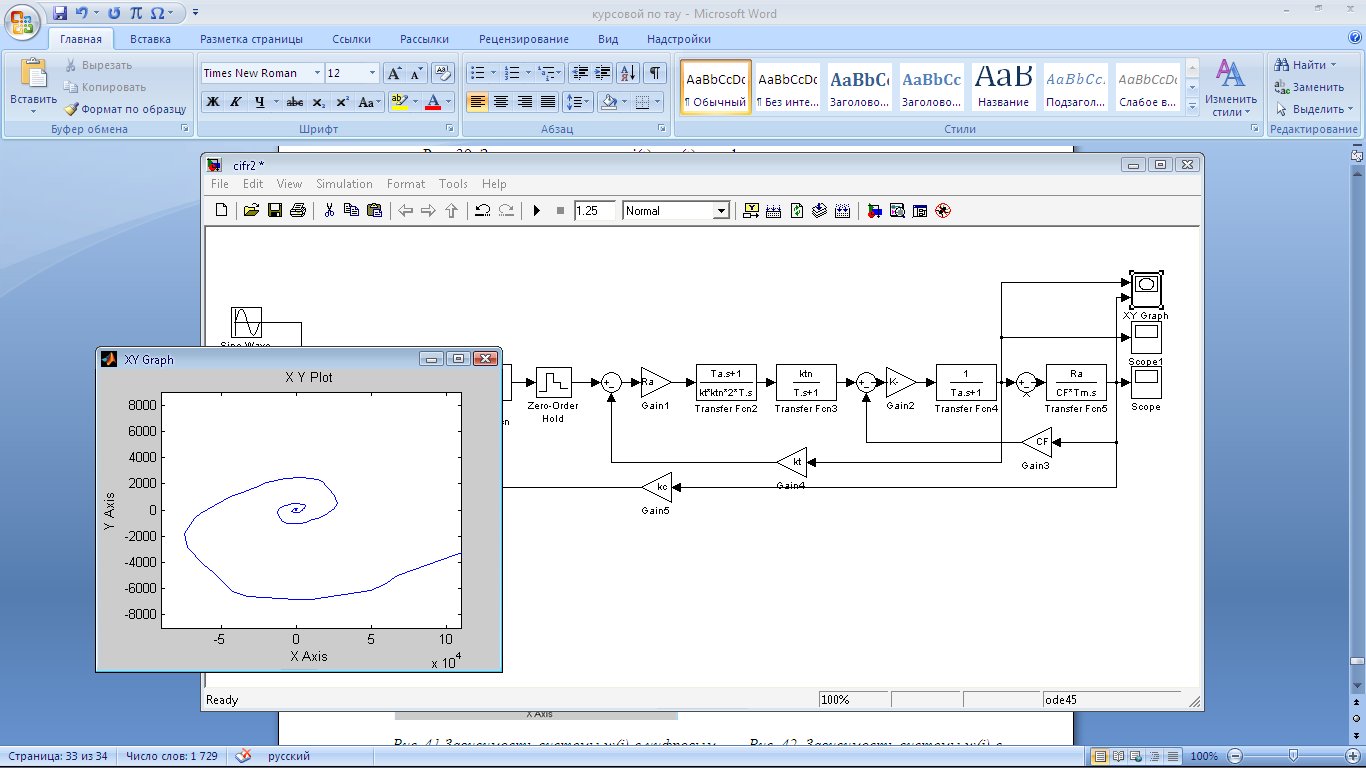
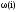Рис. 46 Зависимость системы с Рис.47 Зависимостьсистемы с

цифровым регулятором скорости цифровым регулятором скорости

при T = 0.05*Ta при T = 0.5*Ta

10.1.6. Определение коэффициента передачи

• Численным методом

- амплитуда основной гармоники:

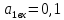
- амплитуда сигнала на выходе системы:

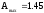
Т.о. коэффициент передачи

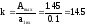
• По ЛАЧХ

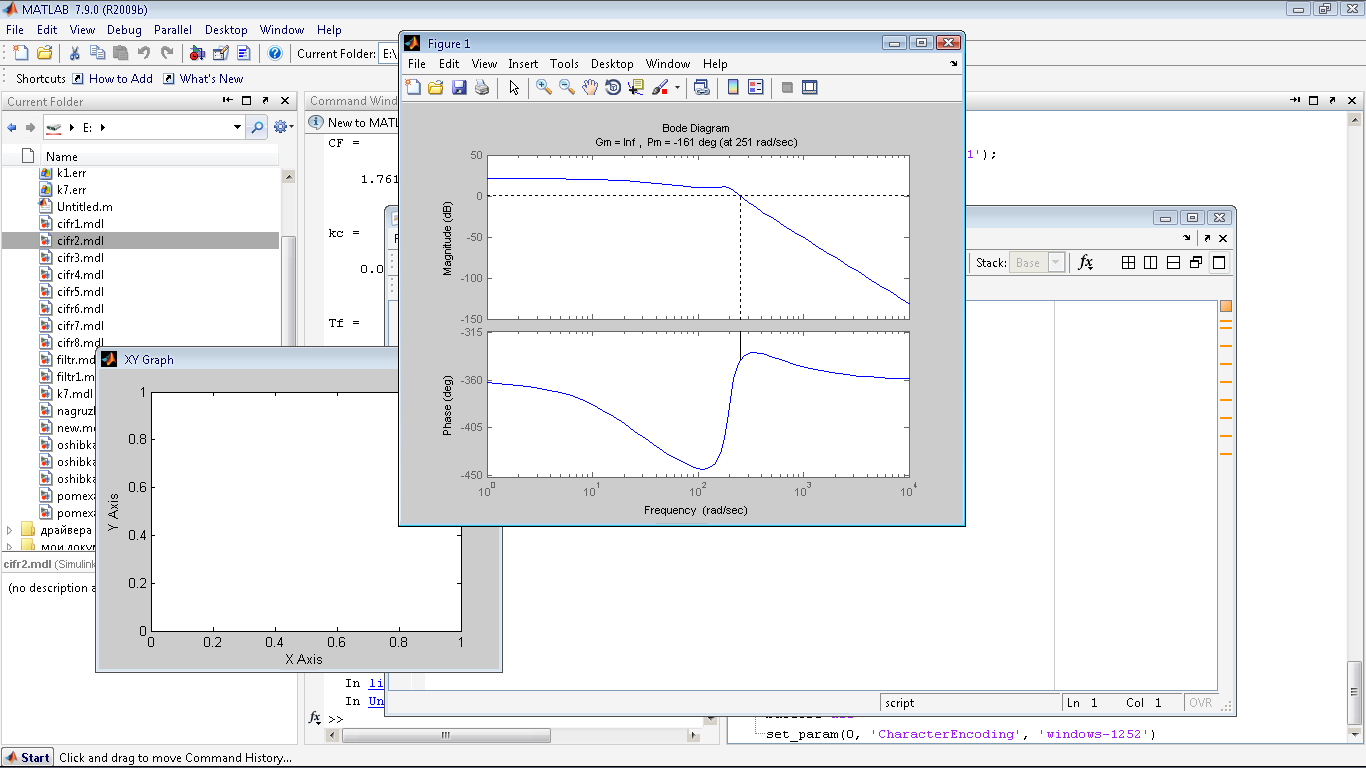
Рис. 21 ЛАЧХ

По графику найдем L(w): 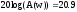, тогда коэффициент передачи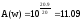

10.2. Билинейные преобразования

10.2.1. Найдем запасы устойчивости по амплитуде и по фазе

Рис. 50 Структурная схема для определения запасов

T = 0.05*Ta

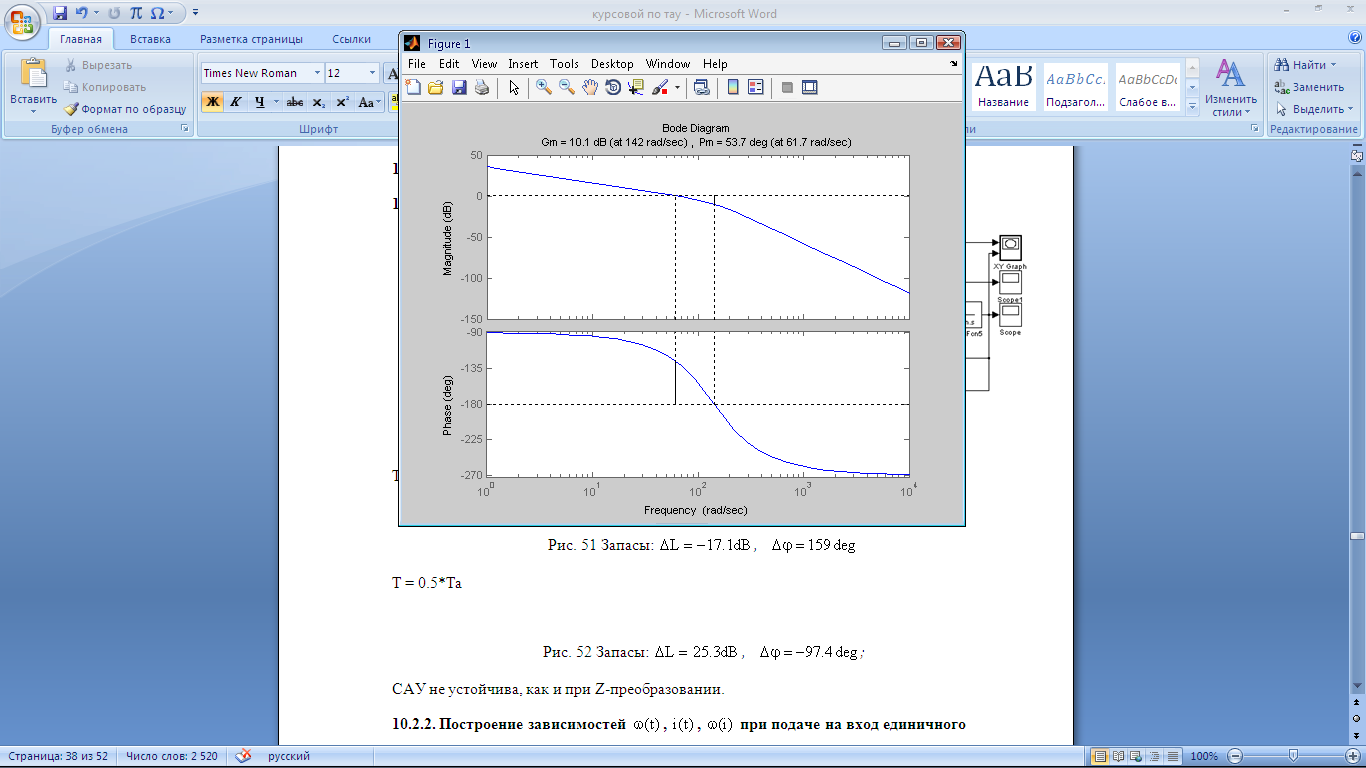
Рис. 51 Запасы: ,

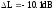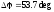
T = 0.5*Ta

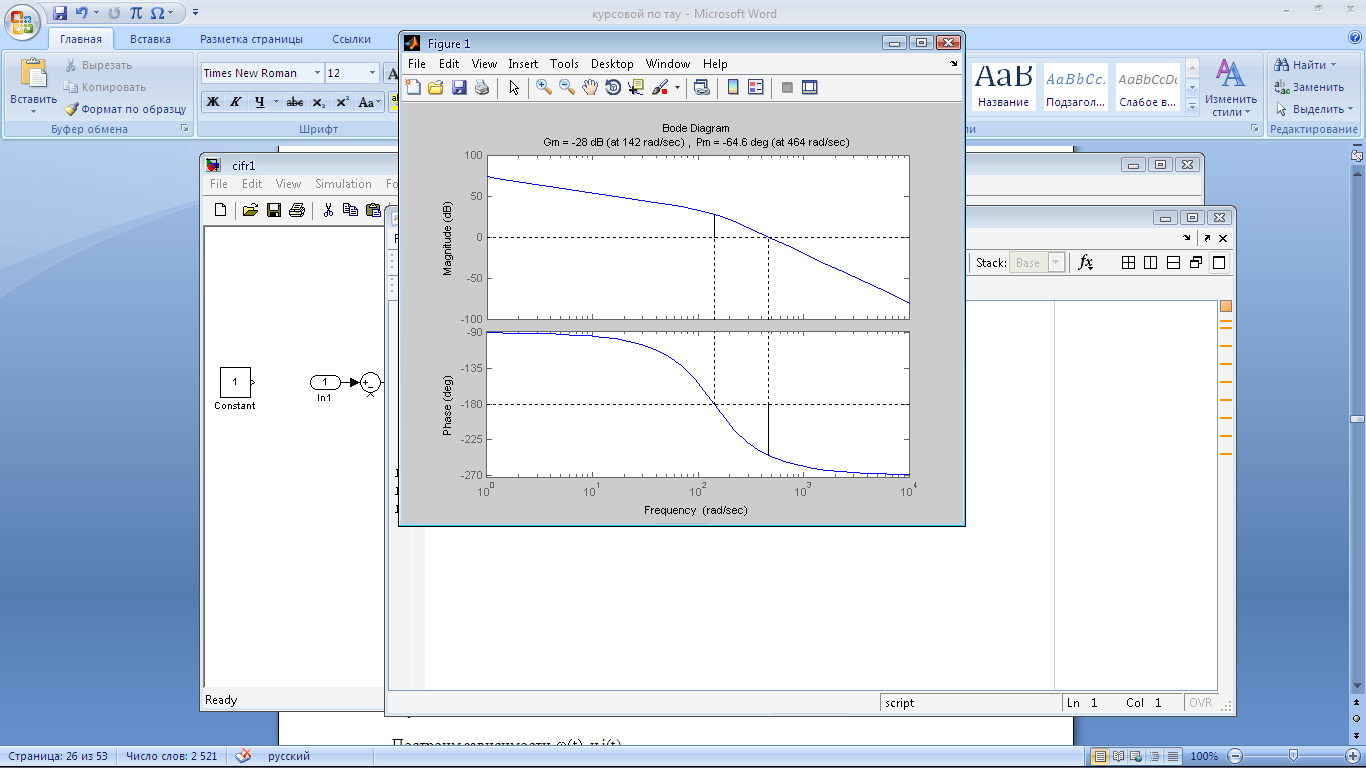
_{Рис. 25 Запасы:}

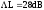
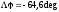
система неустойчива

САУ не устойчива, как и при Z-преобразовании.

10.2.2. Построение зависимостей ,,при подаче на вход единичного ступенчатого сигнала

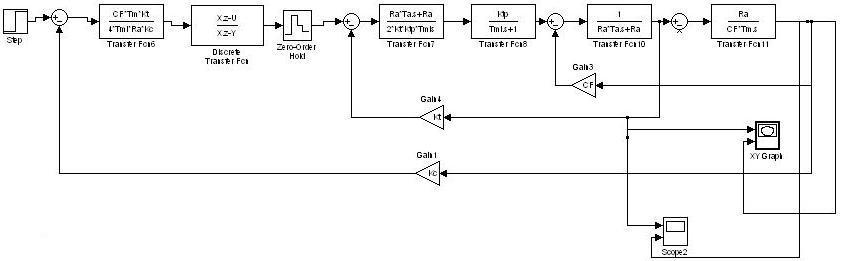
Рис. 53 Структурная схема

T = 0.05*Ta

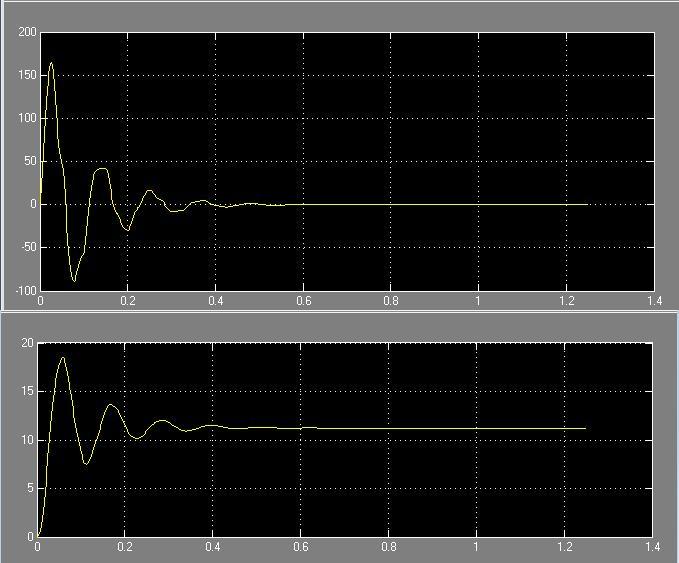
Рис. 54 Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

Из графика можно определить получившиеся показатели качества:

- перерегулирование:

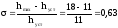
- время регулирования:

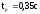
T = 0.5*Ta

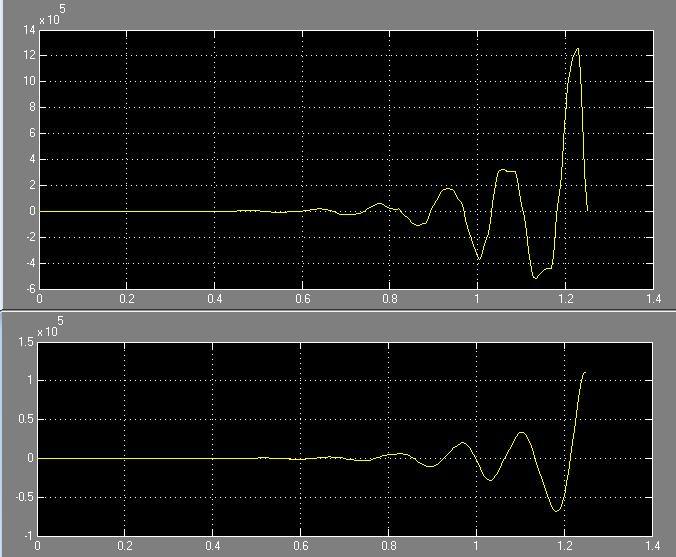
Рис. 55 Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

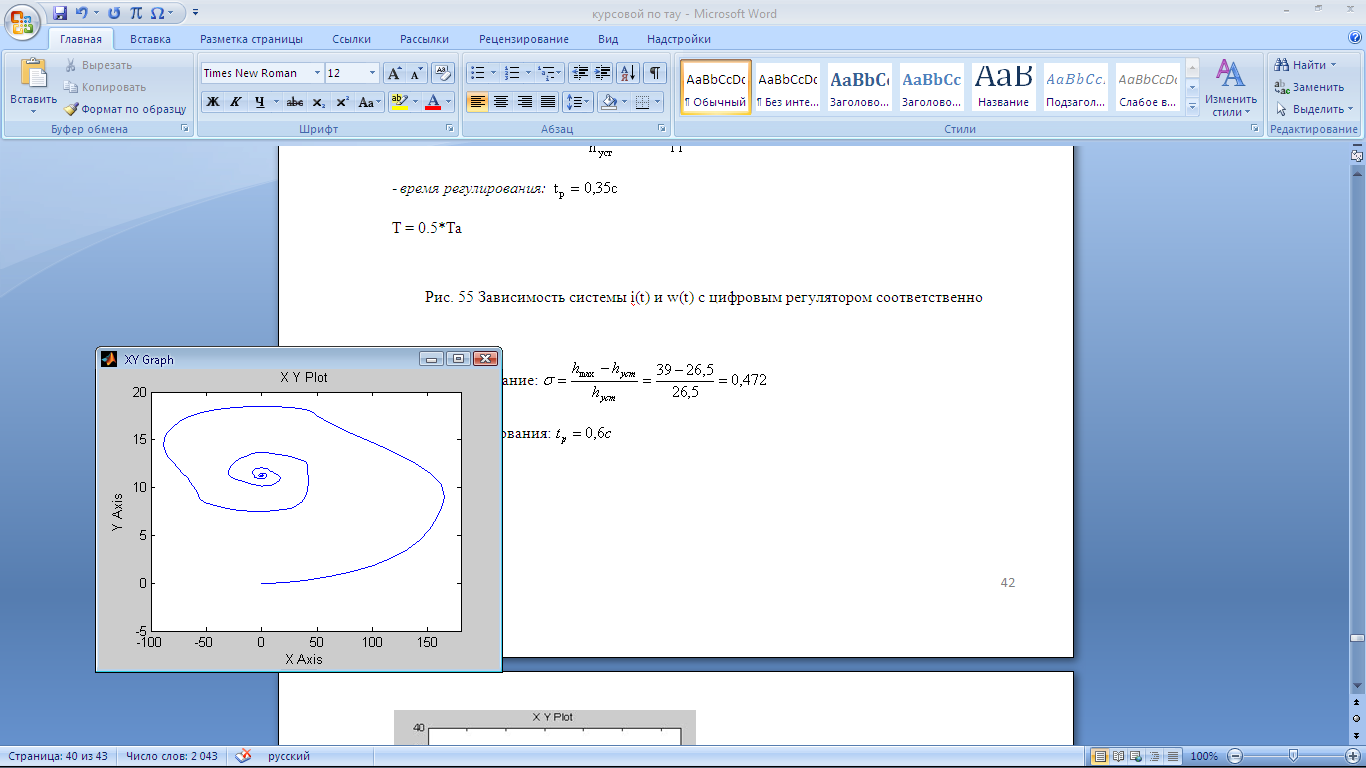
Рис. 56 Зависимость 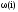системы с Рис.57 Зависимостьсистемы с

цифровым регулятором скорости цифровым регулятором скорости

при T = 0.05*Ta при T = 0.5*Ta

Подтверждаем данными билинейными преобразованиями, что при Т=0.5Та система также неустойчива, как и при Z-преобразованиях.

Перерегулирование больше требуемого, следовательно, нужно поставить фильтр

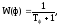
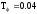
T =0.05*Ta

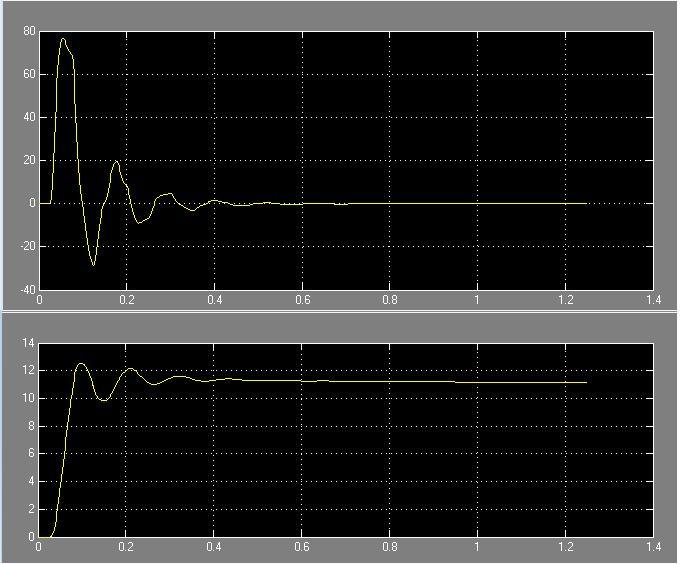
Рис. 58 Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

- перерегулирование:

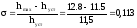
- время регулирования:

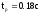
T =0.5*Ta

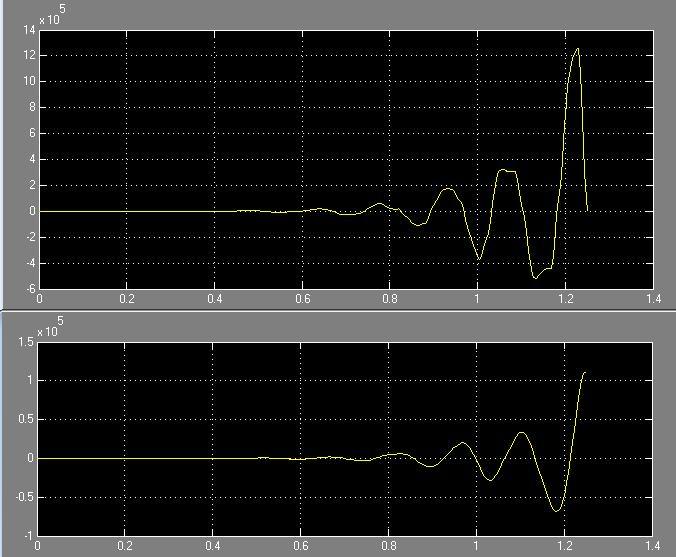
Рис. 59 Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

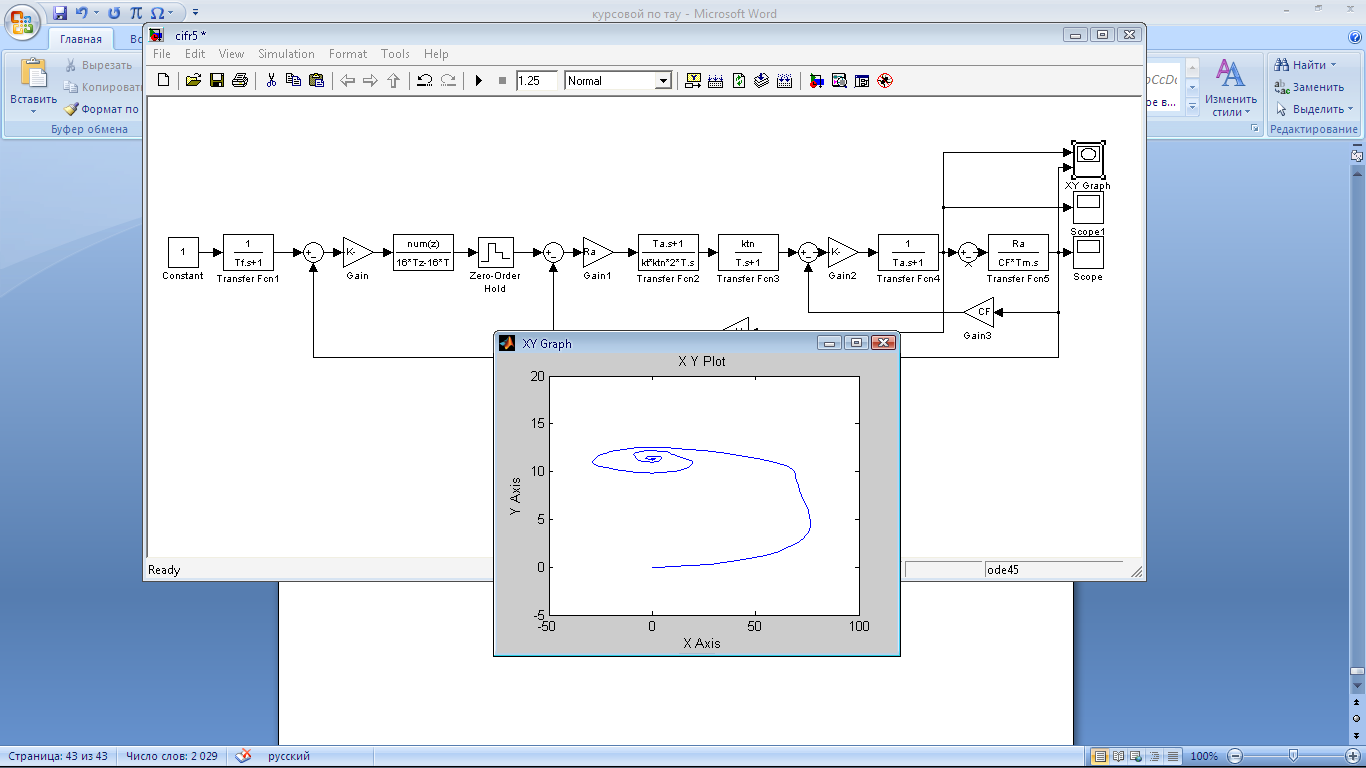
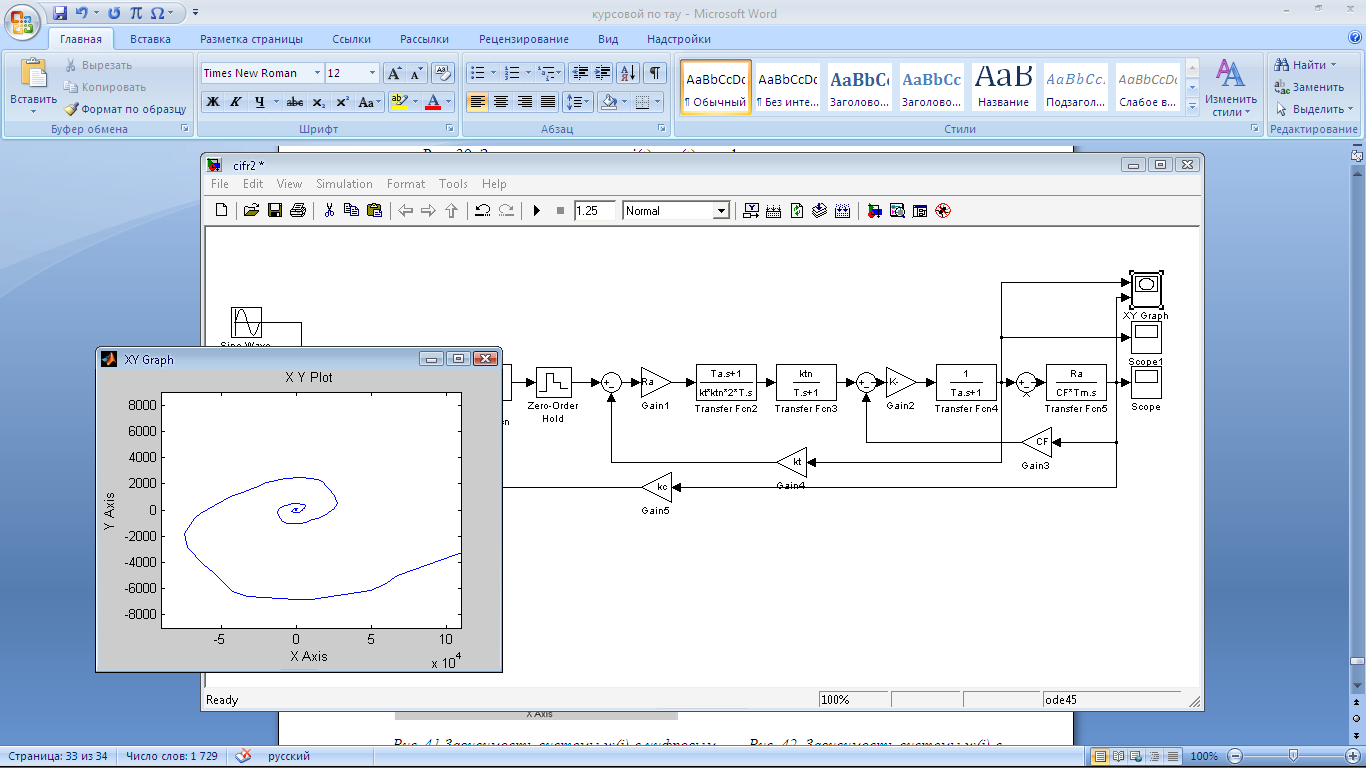
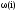Рис. 60 Зависимость системы с Рис.61 Зависимостьсистемы с

цифровым регулятором скорости цифровым регулятором скорости

при T = 0.05*Ta при T = 0.5*Ta