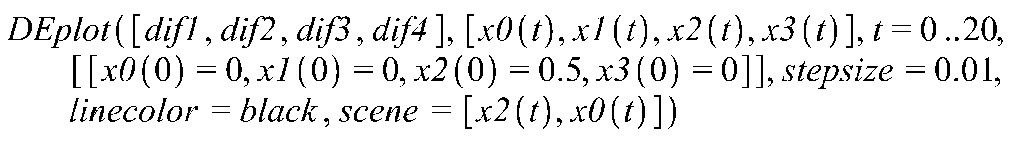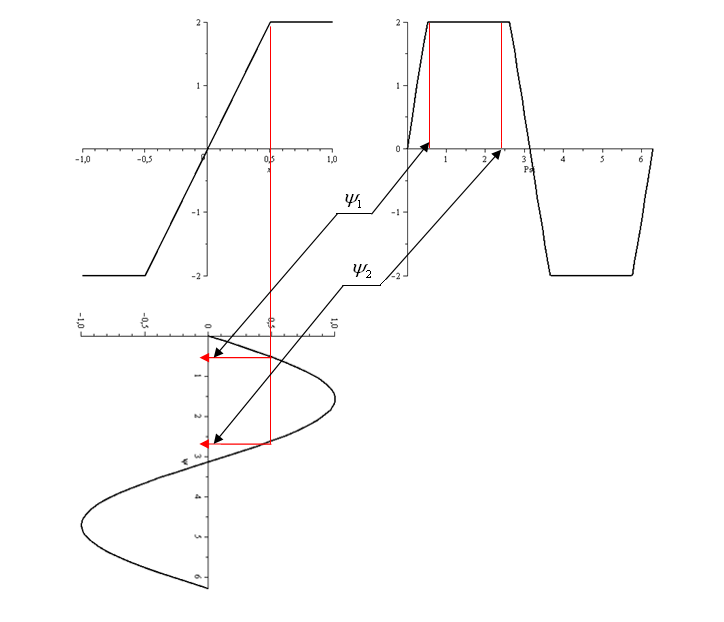
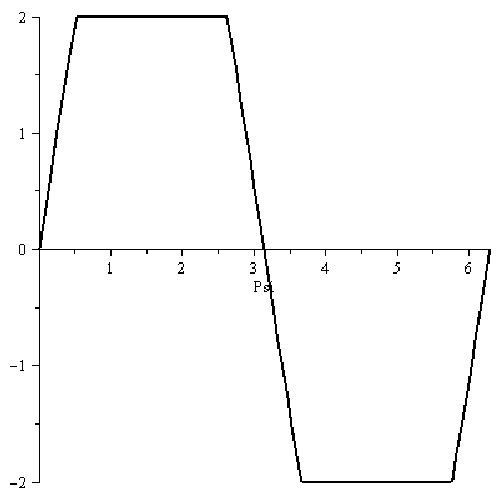
1. Построить график сигнала на выходе нелинейного звена системы, если на его вход поступает гармонический сигнал .

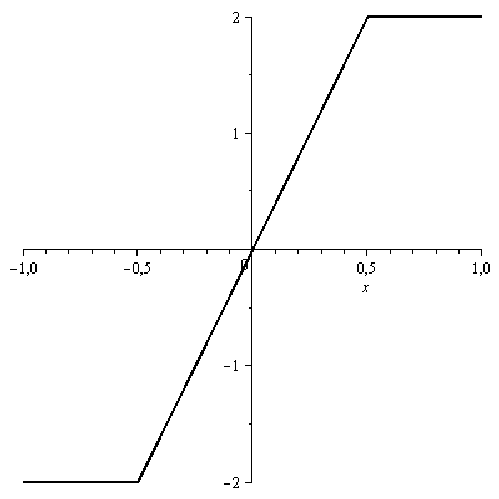
Задано нелинейное звено с характеристикой типа «ограничение».

Воспользуемся Maple:

>

>

>

>

>

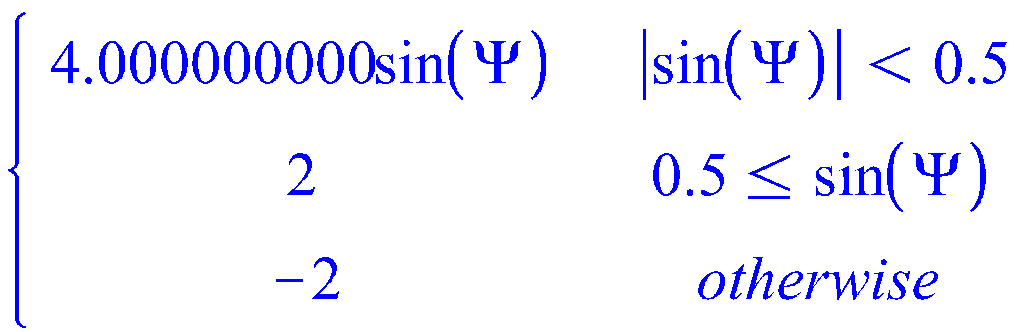
2. Вычислить коэффициенты гармонической линеаризации и для заданного нелинейного звена системы.

Вычисляем первый интеграл:

Вычисляем второй интеграл:

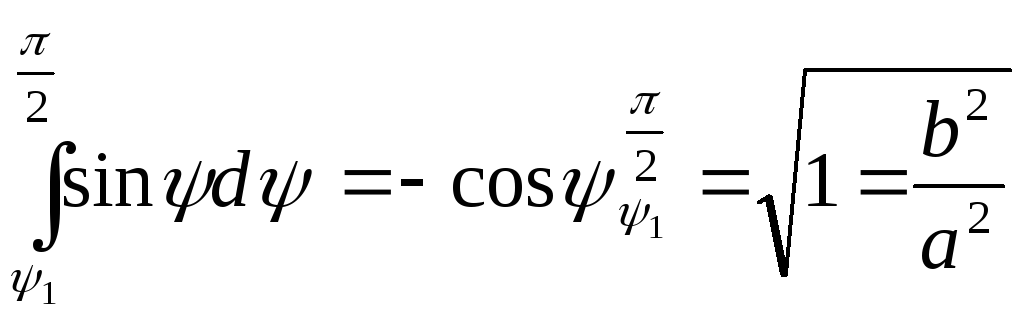
Окончательно получаем:

при

при

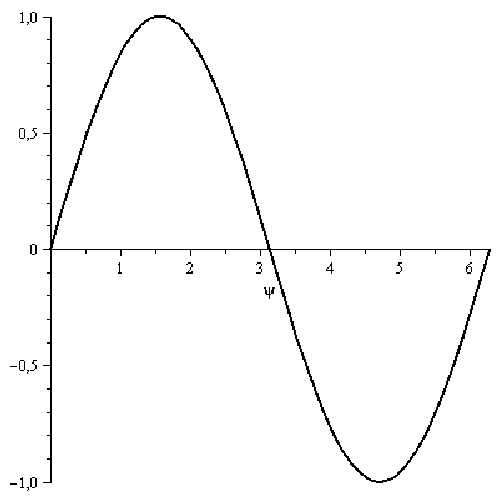
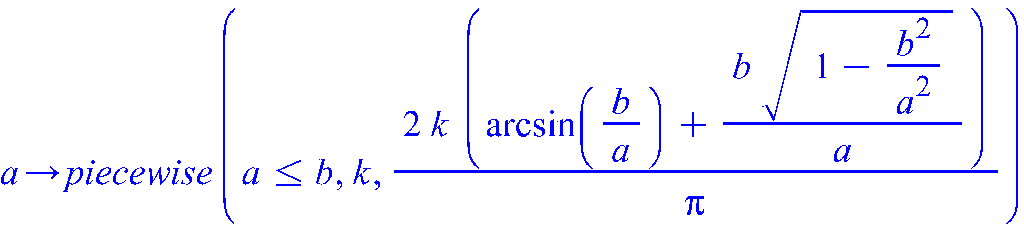
3. Построить графики функций и , используя пакет символьных вычислений Maple.

>

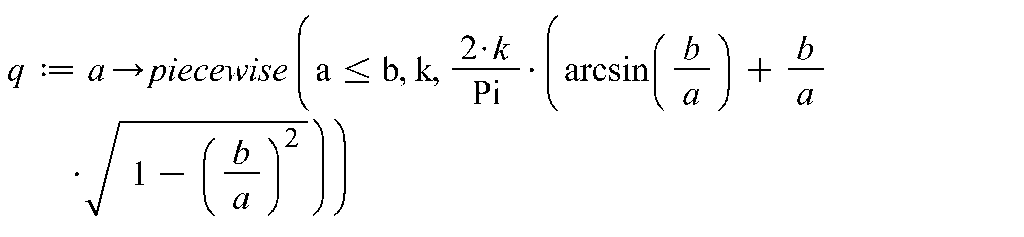
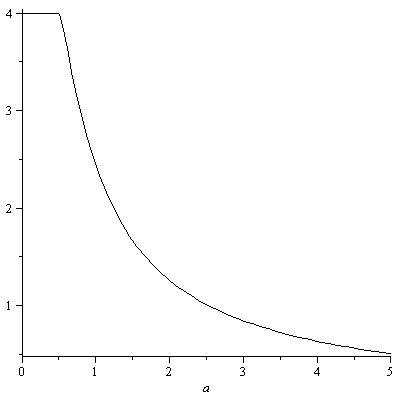
4. Получить уравнение динамики гармонически линеаризованной замкнутой системы.

Преобразуем заданную структурную схему.

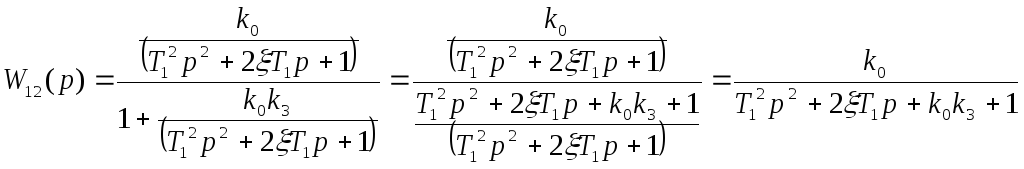
Таким образом, мы преобразовали заданную структурную схему к виду:

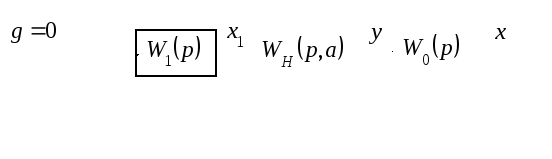
где

Пусть:

Далее последовательно получаем:

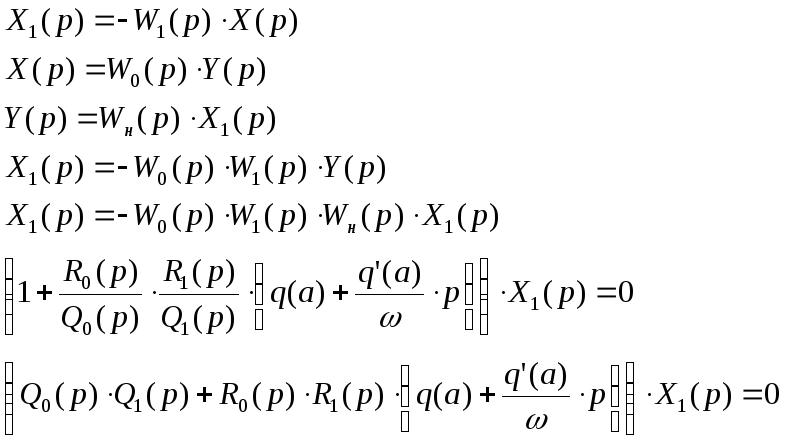
Так как , то получаем:

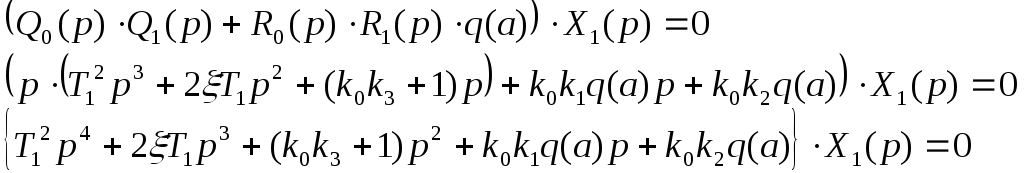
5. Определить приближенные и точные значения амплитуды и частоты периодических процессов в заданной автоматической системе, используя пакет символьных вычислений Maple.

Запишем характеристическое уравнение замкнутой гармонически линеаризованной системы:

Осуществим подстановку :

В полученном выражении выделим действительную и мнимую части:

П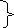риравниваем действительную и мнимую части к нулю:

Из второго уравнения выразим :

Подставляем в первое уравнение:

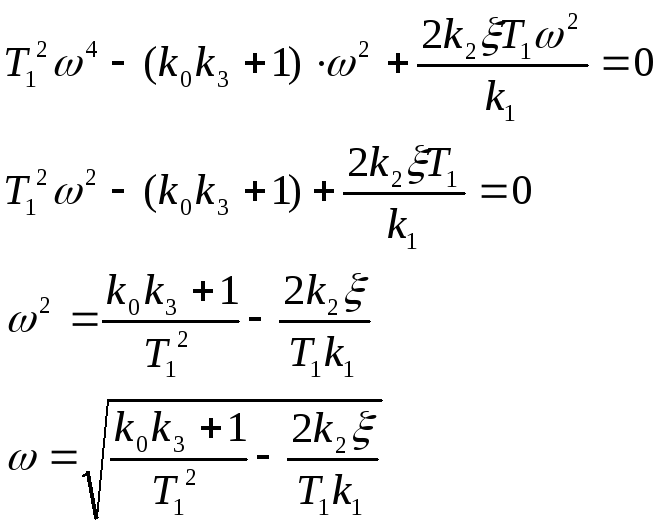
Теперь, с учетом выражения для частоты , выразим :

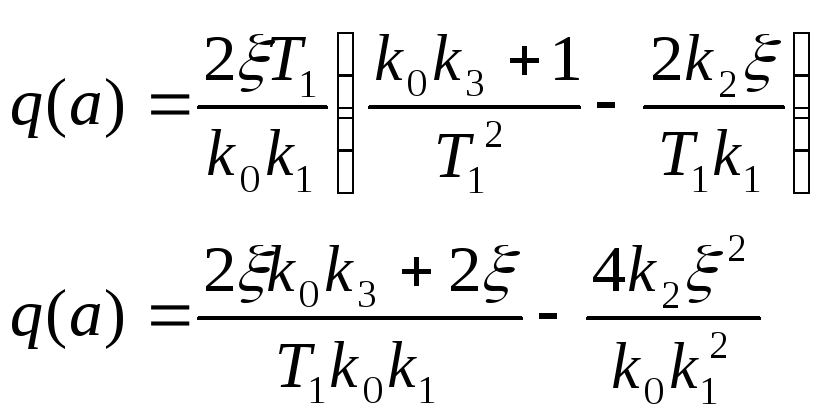
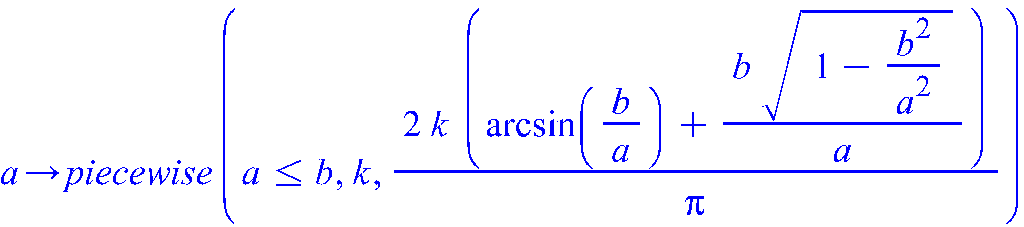
Теперь воспользуемся Maple:

>

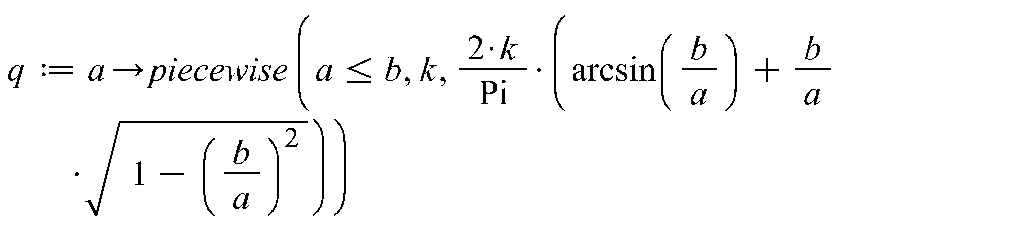
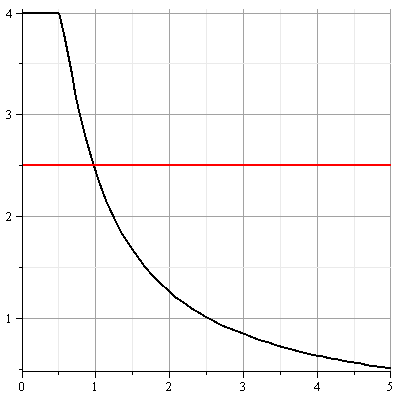
Исходя из графика, приближенное значение амплитуды будет:

Теперь найдем точные значения амплитуды и частоты:

Таким образом:

6. Исследовать периодические процессы в автоматической системе на устойчивость

с помощью критерия устойчивости Гурвица

Задано характеристическое уравнение:

Введем обозначения:

, , , ,

Составляем матрицу Гурвица:

Выписываем определитель матрицы:

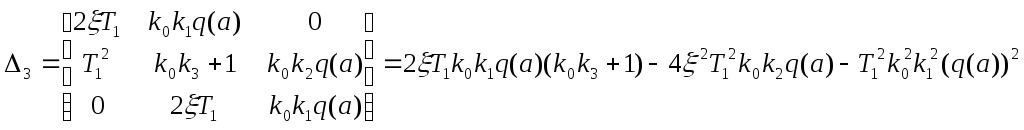
Находим знак частной производной определителя. Для этого воспользуемся Maple:

>

>

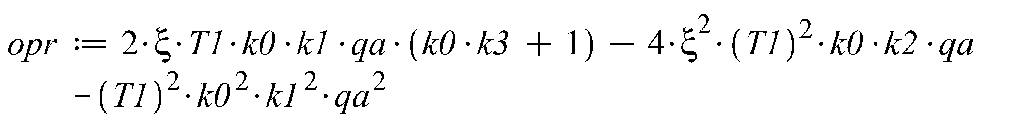
Так как , то следовательно:

Для периодического процесса имеем:

То есть для периодического процесса выполняется первое условие устойчивости по критерию Гурвица.

Находим частное деление на +.

0

Таким образом

_{Находим корни с помощью Maple:}

>

Таким образом выполняется второе условия критерия Гурвица и, следовательно, колебательному процессу с частотой и амплитудой соответствуют автоколебания в системе.

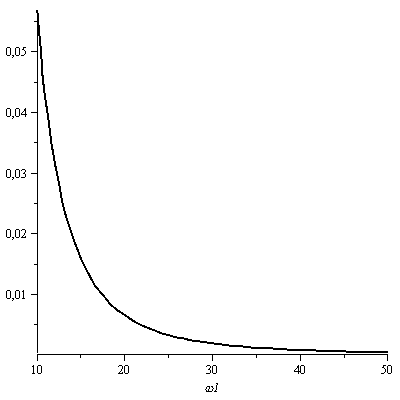
7. Проверить условие фильтра линейной части системы.

Для проверки выполнения условия фильтра линейной части системы, прежде всего нужно выписать операторную передаточную функцию линейной части исследуемой системы:

В последнем равенстве выполняем подстановку :

Воспользуемся Maple:

>

8. Записать математическую модель автоматической системы в виде системы дифференциальных уравнений в нормальной форме Коши.

Для того чтобы записать математическую модель исследуемой системы в нормальной форме Коши обратимся к исходной структурной схеме.

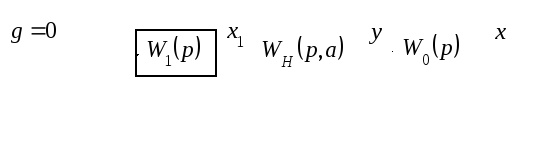
Где

Для удобства расчета разобьем первое звено на два:

Из структурной схемы следует, что .

Введем обозначение: . Тогда математическая модель исследуемой автоматической системы в нормальной форме Коши имеет вид:

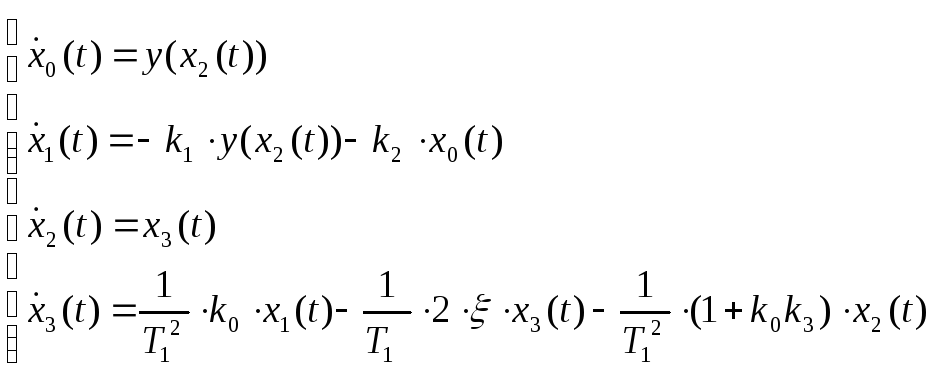
где

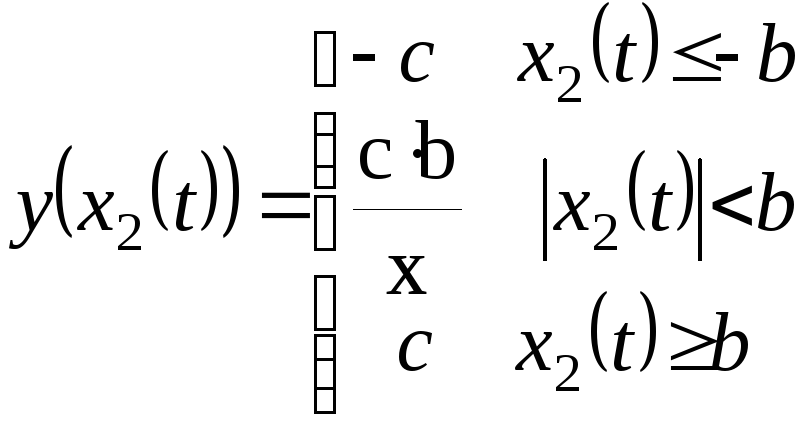
9. Выполнить моделирование процессов в исследуемой системе управления, используя пакет символьных вычислений Maple.

>

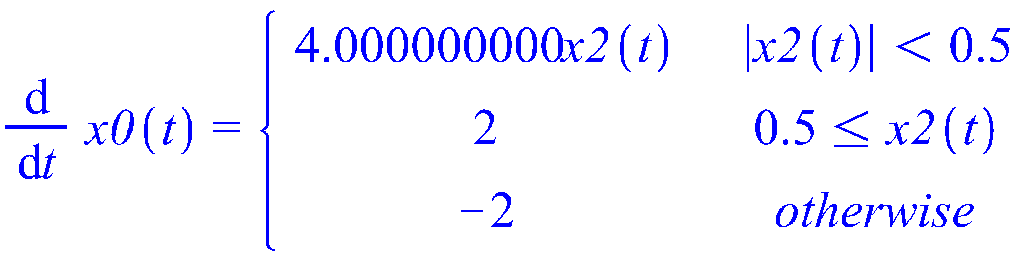
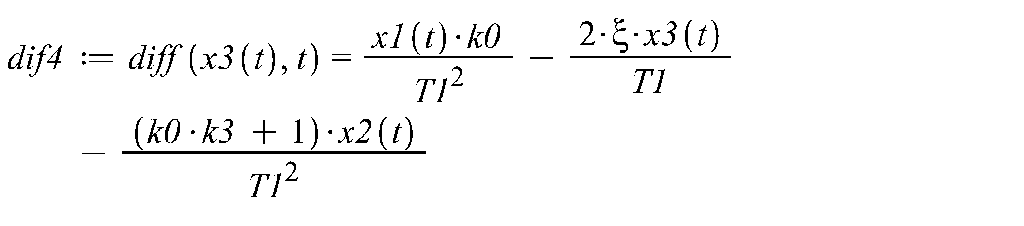
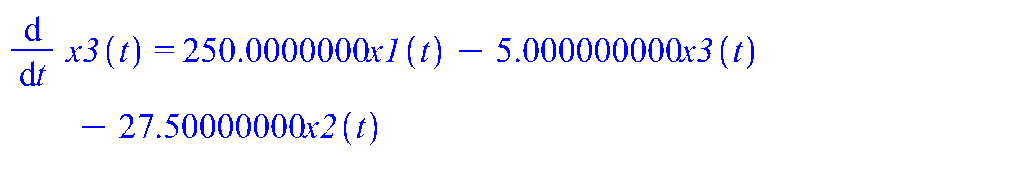
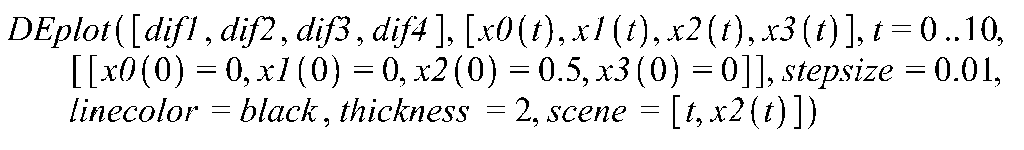
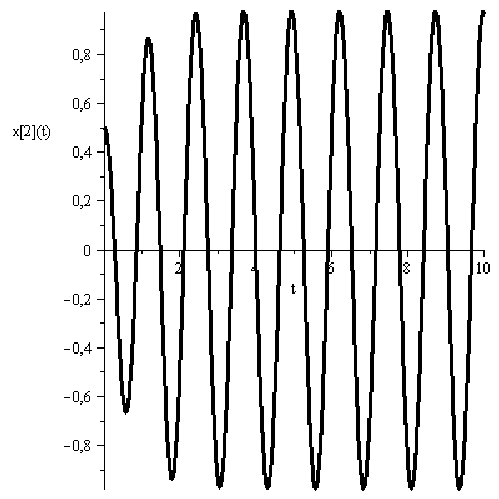
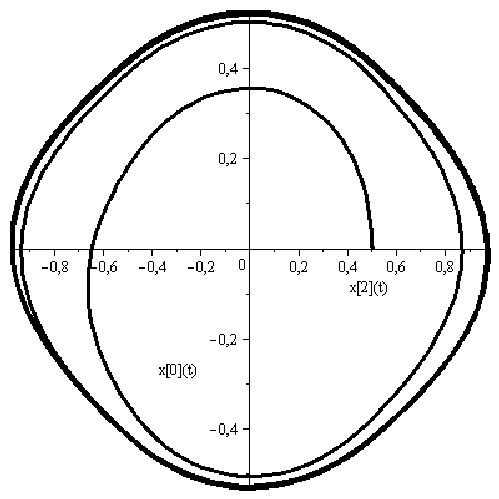
10. Выполнить построение фазовой траектории исследуемой системы управления, используя пакет символьных вычислений Maple.

14