курсовая работа / opredelenie_ustoychivosti_sistemy_po_kriteriyu_gurvica

Министерство общего и профессионального

образования Российской Федерации.

Пермский Государственный Технический Университет

Чайковский филиал

Кафедра Микропроцессорных средств автоматизации

КУРСОВОЙ ПРОЕКТ

по дисциплине «теория автоматического управления»

Таблица № 2, Вариант № 5

Выполнил: студент группы БА-04

Михеев Г.В.

Проверил: доцент кафедры МСА

Андриевская Н. В.

г. Чайковский 2007 г.

Содержание.

1. Анализ исходной непрерывной системы;

2. Синтез непрерывной системы методом ЛАЧХ;

3. Синтез непрерывной системы с модальным регулятором;

4. Синтез цифровой системы по критерию быстродействия.

Задание по курсовому проектированию:

Астатическая система:

Параметры и требуемые показатели качества:

Минимальный запас устойчивости

1. Анализ исходной непрерывной системы.

Объект управления задан структурной схемой:

В соответствии со структурной схемой передаточная функция статической системы в разомкнутом состоянии имеет вид:

Передаточная функция замкнутой системы имеет вид:

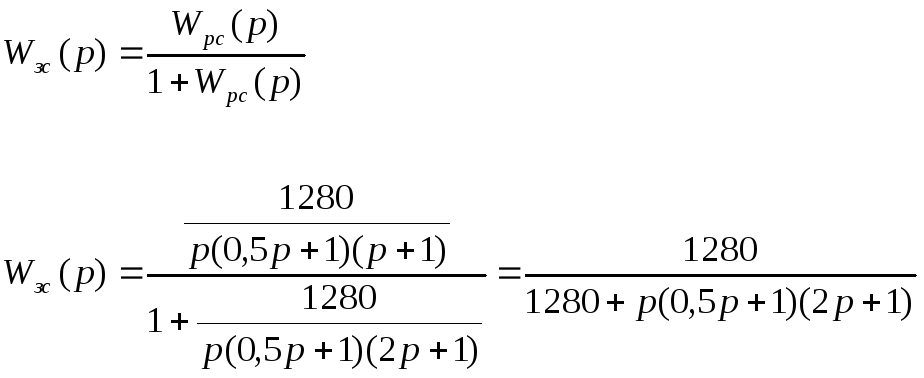
Определим устойчивость системы по критерию Гурвица:

Система автоматического управления будет устойчивой тогда и только тогда, когда при положительном старшем коэффициенте характеристического уравнения все определители матрицы Гурвица будут положительными.

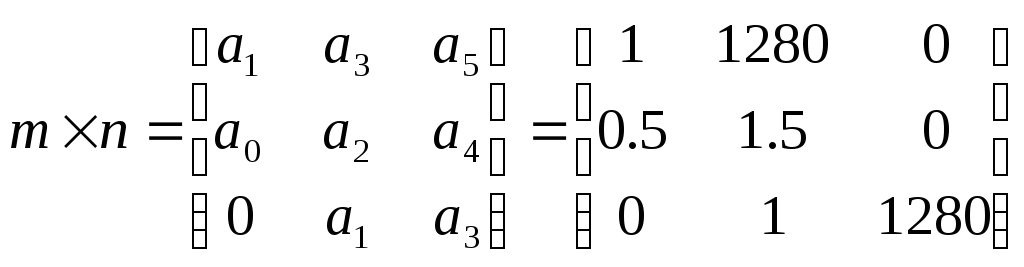
Условия:

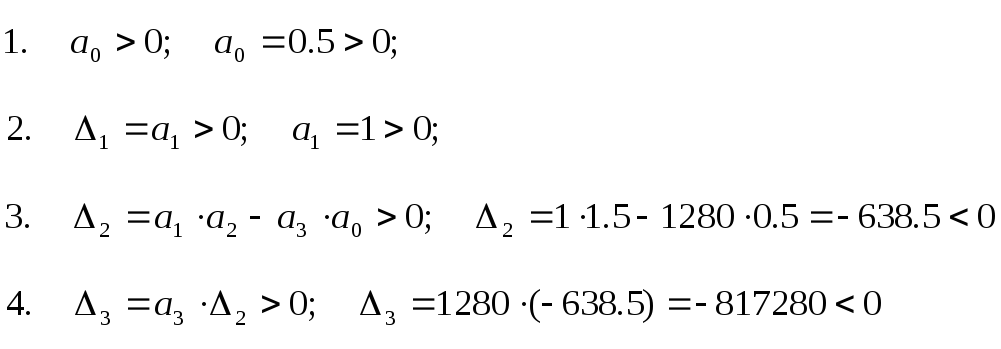
Система не устойчива.

График переходного процесса, исходной непрерывной системы (объекта) Приложение 1

2. Синтез непрерывной системы методом ЛАЧХ.

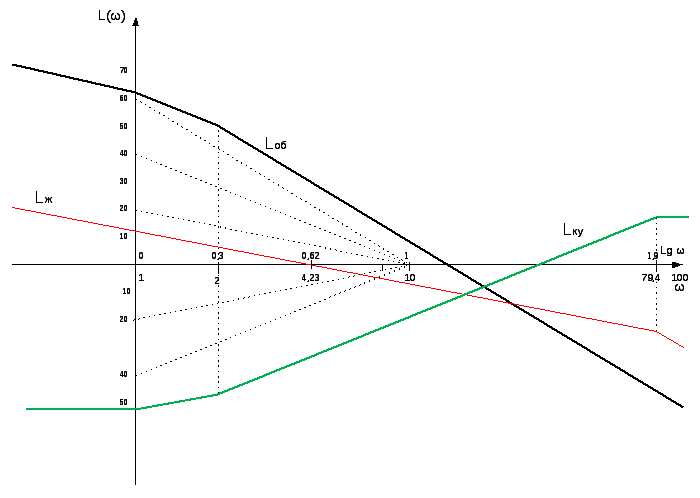
1. Определим координаты ЛАЧХ объекта:

Так как система астатическая, то начальный участок ЛАЧХ имеет наклон

-20 дБ/дек., проходящий через точку

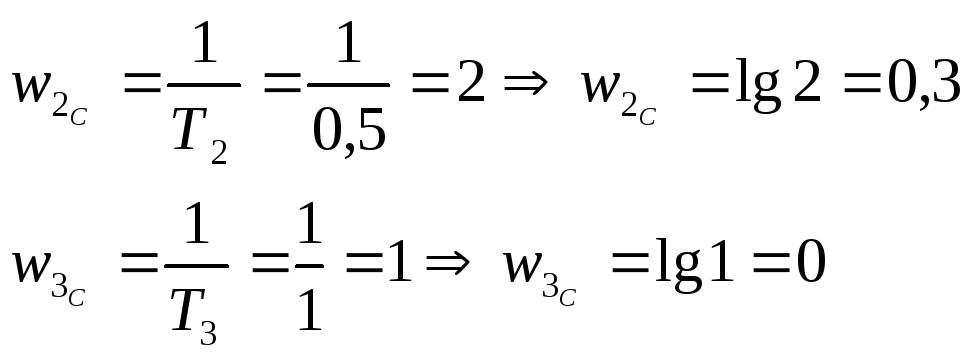
2. Определим координаты желаемой ЛАЧХ (из графика зависимости рис):

Теперь требуется найти рациональную протяженность этого участка ЛАЧХ. Для этого найдем на номограмме (приложение 3) кривую с индексом 1.06 Впишем эту кривую в соответствующий прямоугольник. (В нижней части это будет кривая с индексом 1,06 - 1,0 = 0,06.)

Крайние значения участка ЛАЧХ с наклоном -20 дБ/дек. составляют: L₁ =24 дБ и L₂ =-24 дБ (Это крайние значения L₁ и L₂). При этом гарантируется запас устойчивости по фазе Δφ°=244°-116°=128°.

2. Определим наклон ЛАЧХ регулятора:

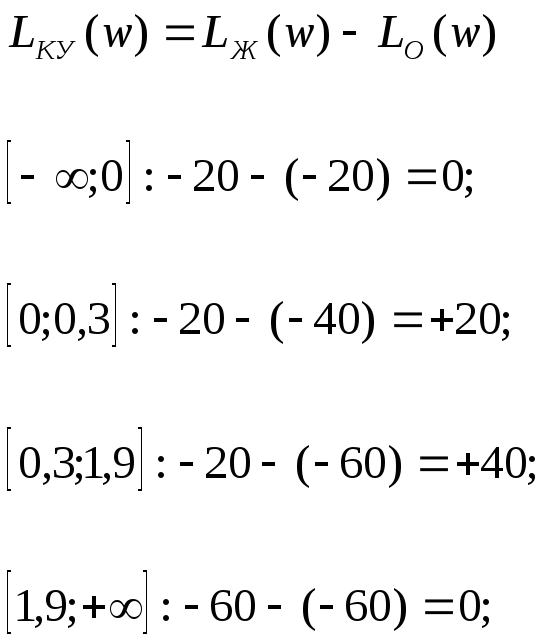
Лачх

2. По ЛАЧХ определим передаточную функцию регулятора:

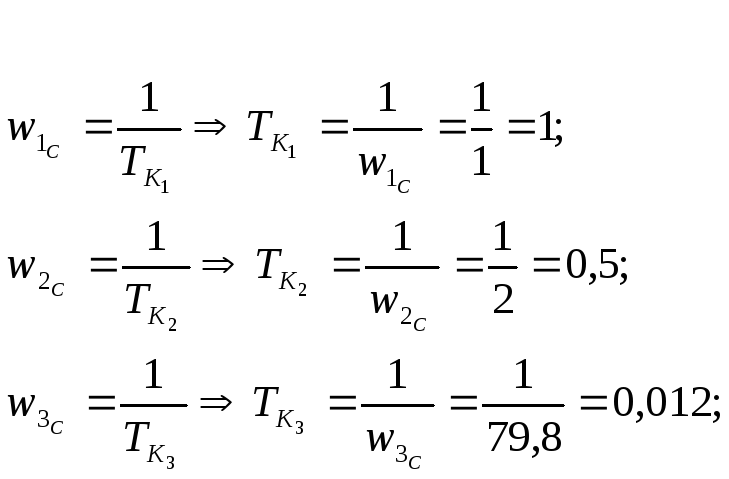
График переходного процесса с регулятором представлен в рис приложение 2

Показатели качества: ; t_пп=0,8с

3. Синтез непрерывной системы с модальным регулятором.

Схема переменных состояний:

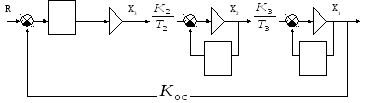
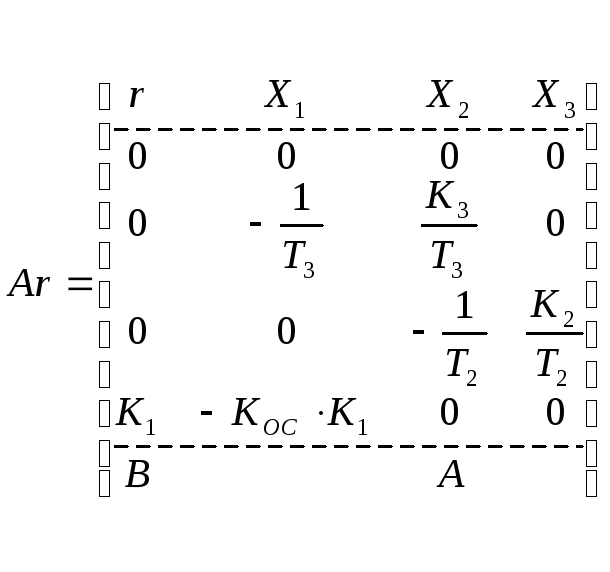
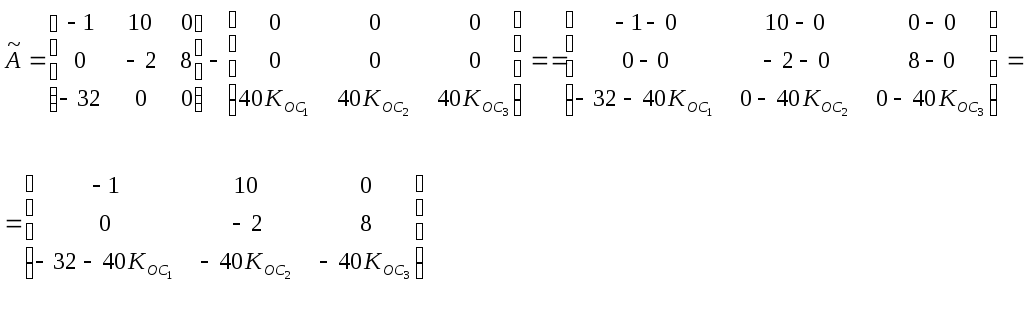
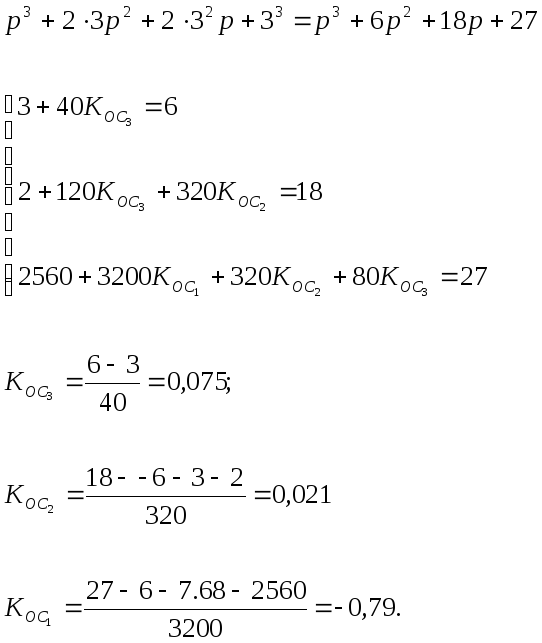
схема с модальным регулятором.

График переходного процесса с модальным регулятором приложение 3

Показатели качества: ; t_пп=4,3с

Расчет цифрового регулятора

Расчет приведенной дискретной передаточной функции разомкнутой системы подстановкой Тастина:

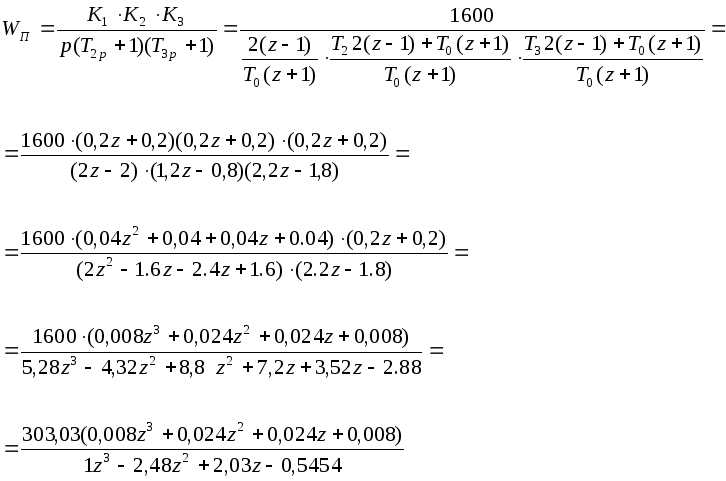
Расчет передаточной функции регулятора для оптимального быстродействия:

,

где

График переходного процесса с цифровым регулятором приложение 4

Показатели качества: ; t_пп= 7с

Приложение 1

График переходного процесса, исходной непрерывной системы (объекта) .

Приложение 2

График переходного процесса с регулятором представлен в рис.

Приложение 3

График переходного процесса с модальным регулятором

Приложение 4

График переходного процесса с цифровым регулятором