
- •Раздел 2. Элементы векторной алгебры
- •10. Проекции вектора
- •11. Скалярное произведение Основные понятия и определения
- •Свойства скалярного произведения векторов:
- •12. Скалярное произведение векторов, заданных координатами в ортонормированном базисе
- •Вычисление длины вектора и угла между векторами
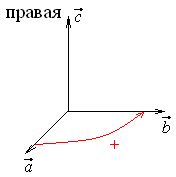
- •14. Ориентация пространства. Правая и левая тройки веторов
- •15. Векторное произведение: определение, свойства
- •Свойства векторного произведения
- •16. Векторное произведение в ортонормированном репере
- •17. Геометрический смысл векторного произведения:
- •18. Двойное векторное произведение
- •19. Смешанное произведение векторов
- •Свойства смешанного произведения
- •20. Геометрический смысл смешанного произведения
- •21. Смешанное произведение в ортонормированном базисе
- •Приложения произведений векторов
16. Векторное произведение в ортонормированном репере
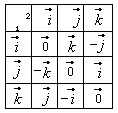
Даны
векторы
![]() ,
,
![]() ,
,
т.е.
![]() ,
,
![]()
Векторное произведение ортов (см. табл.)
Тогда
![]() =(
=(![]() )(
)(![]() )=
)=
![]() =
=
=![]() .
.
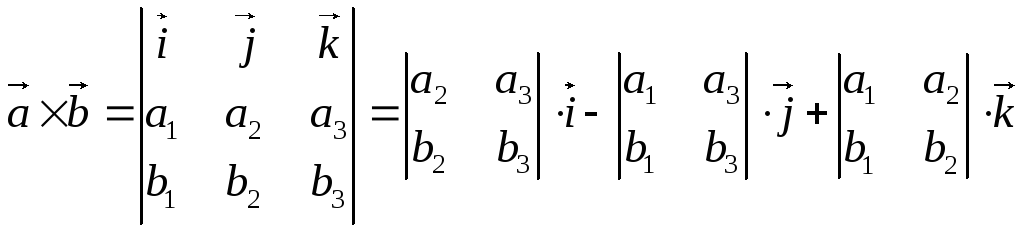 . (8.10)
. (8.10)
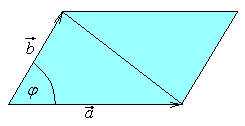
17. Геометрический смысл векторного произведения:
1) Площадь
параллелограмма.
![]() – формула площади параллелограмма.
– формула площади параллелограмма.
![]() – модуль векторного
произведения по определению.
– модуль векторного
произведения по определению.
Тогда
![]() .
.
Площадь
параллелограмма, построенного на
векторах
![]() и
и
![]() как на сторонах, равна модулю векторного
произведения этих векторов.
как на сторонах, равна модулю векторного
произведения этих векторов.
![]() ,
,
2) Площадь
треугольника:
![]() .
.
Площадь
треугольника, построенного на векторах
![]() и
и
![]() как на сторонах, равна половине модуля
векторного произведения этих векторов.
как на сторонах, равна половине модуля
векторного произведения этих векторов.
Пример 2. Вычислим площадь грани АВС тетраэдра DАВС, если А(1;2;1), В(4;1;2), С(1;5;3), D(2;3;1).
Решение.
![]() .
.
Найдем координаты
![]() и
и
![]() ,
на которых построен треугольник АВС,
как на сторонах:
,
на которых построен треугольник АВС,
как на сторонах:
![]() (4–1;1–2;2–1),
(4–1;1–2;2–1),
![]() (1–1;5–2;3–1), тогда
(1–1;5–2;3–1), тогда
![]() (3;–1;1),
(3;–1;1),
![]() (0;3;2).
(0;3;2).
Вычислим векторное
произведение
![]()
![]() и его длину:
и его длину:

![]()
![]() (–5;–6;9),
(–5;–6;9),
|![]()
![]() |=
|=![]() ,
,
![]() (кв.ед.).
(кв.ед.).
Механический
смысл
векторного произведения: Моментом силы
![]() относительно точки О
называется вектор
относительно точки О
называется вектор
![]() ,
имеющий начало в точке О,
направленный перпендикулярно к плоскости,
определяемой точкой О
и вектором
,
имеющий начало в точке О,
направленный перпендикулярно к плоскости,
определяемой точкой О
и вектором
![]() .
Длина вектора равна произведению длины
вектора
.
Длина вектора равна произведению длины
вектора
![]() на плечо h
– перпендикуляра, опущенного из точки
о на направление вектора
на плечо h
– перпендикуляра, опущенного из точки
о на направление вектора
![]() )
или
)
или
![]() ,
где
,
где
![]() – радиус-вектор точки приложения силы
– радиус-вектор точки приложения силы
![]() .
.
18. Двойное векторное произведение
Определение 30.
Двойным
векторным произведением
называется вектор
![]() .
.
Пример 3..
Вычислить двойное
векторное произведение
![]() (1;3;5),
(1;3;5),
![]() (–1;–2;0),
(–1;–2;0),
![]() (0;4;3).
(0;4;3).
 ,
,
 .
.
Свойства двойного векторного произведения (со скалярным):
1.
![]() =
=![]() (8.11)
(8.11)
2.
![]()
![]()
3.
![]() тождество Якоби.
тождество Якоби.
19. Смешанное произведение векторов
Рассмотрим
векторно-скалярное произведение векторов
![]() ,
,
![]() и
и
![]() ,
составленное следующим образом:
,
составленное следующим образом:
![]() .
Первые два вектора умножаются векторно,
а их результат на третий вектор скалярно.
Такое произведение называется
векторно-скалярным, или смешанным,
произведением трех векторов.
.
Первые два вектора умножаются векторно,
а их результат на третий вектор скалярно.
Такое произведение называется
векторно-скалярным, или смешанным,
произведением трех векторов.
Определение 31.
Смешанным
(векторно-скалярным) произведением трех
векторов
![]() ,
,
![]() и
и
![]() называется
число
называется
число
![]() ,
полученное в результате векторного
произведения векторов
,
полученное в результате векторного
произведения векторов
![]() и
и
![]() ,
умноженного скалярно на вектор
,
умноженного скалярно на вектор
![]() .
.
Обозначение: ![]() =
=![]() (8.12)
(8.12)
Из определения
следует:
![]() ,
или
,
или
![]() ,
или
,
или
![]() ,
то
,
то
![]() (самостоятельно)
(самостоятельно)
Пример 4. Вычислим смешанное произведение ортов (по определению).
![]() .
.
Свойства смешанного произведения
1. Смешанное произведение не зависит от порядка векторного и скалярного умножения, т.е. не изменится при перестановке знаков умножения.
![]() =
=![]() (8.13)
(8.13)
Доказательство.
![]() =
=![]() ,
,
![]() =
=![]() ,
причем одного знака, так как тройки
,
причем одного знака, так как тройки
![]() ,
,![]() ,
,![]() и
и
![]() ,
,![]() ,
,![]() – обе правые. Значит,
– обе правые. Значит,
![]() =
=![]() .
Отсюда,
.
Отсюда,
![]() =
=![]() .
.
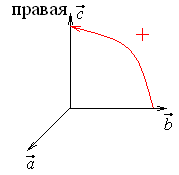
Это свойство позволяет записывать смешанное произведение векторов без знаков векторного и скалярного умножения.
2. Смешанное произведение не изменяется при циклической перестановке множителей:
![]() (8.14)
(8.14)
Доказательство.
1)
![]() ;
2) если тройка векторов
;
2) если тройка векторов
![]() ,
,![]() ,
,![]() – правая, то тройки
– правая, то тройки
![]() ,
,![]() ,
,![]() и
и
![]() ,
,![]() ,
,![]() – тоже правые.
– тоже правые.
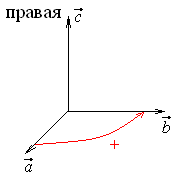

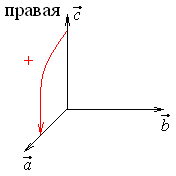
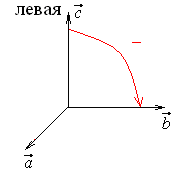
3. Смешанное произведение меняет знак на противоположный при перестановке двух множителей:
![]() ,
,
![]() ,
,
![]() (8.15)
(8.15)
Доказательство. самостоятельно
1)
![]() ;
2) если тройка векторов
;
2) если тройка векторов
![]() ,
,![]() ,
,![]() – правая, то тройки
– правая, то тройки
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]() – левые.
– левые.


4.
Если (![]()
![]()
![]() )0,
то тройка векторов
)0,
то тройка векторов
![]() ,
,![]() ,
,![]() – правая; если (
– правая; если (![]()
![]()
![]() )0,
то тройка векторов
)0,
то тройка векторов
![]() ,
,![]() ,
,![]() – левая.
– левая.
5. Теорема.
Смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны
![]() (8.16)
(8.16)
Доказательство.
1) Дано:![]() .
Докажем, что векторы
.
Докажем, что векторы
![]() ,
,![]() ,
,![]() компланарны.
компланарны.
![]()
![]() =SH=0
а)S=0
или б)Н=0.
=SH=0
а)S=0
или б)Н=0.
а)S=0
![]()
![]() ,
,![]() коллинеарны
коллинеарны
![]() ,
,![]() ,
,![]() компланарны;
компланарны;
б)Н=0
![]() ,
где
,
где
![]()
![]()
![]() ,
,![]() ,
,![]() компланарны.
компланарны.
2) Дано: векторы
![]() ,
,![]() ,
,![]() компланарны. Докажем, что
компланарны. Докажем, что![]() .
.
![]() =0
=0
![]() .
.
Теорема доказана.
6.
Условие
компланарности трех векторов: (![]()
![]()
![]() )=0.
)=0.
