Вычисление длины вектора и угла между векторами
Из
свойства 1
,
в координатах по формуле (8.3):
(8.4)
Пусть
длины векторов:
,
,
Из
определения и формул (8.3)-(8.4) следует,
что
угол между векторами вычисляется по
формуле:
=
. (8.5)
Пример 1. Вычислим косинус угла между ребрами АВ и СD тетраэдра DАВС, если А(1;2;1), В(4;1;2), С(1;5;3), D(2;3;1).
.
Найдем координаты векторов
и
:
(4–1;1–2;2–1),
(2–1;3–5;1–3),
тогда
(3;–1;1),
(1;–2;–2).
Подставим в формулу и вычислим:
,
0,3015
(т.е. 72о).
Определение 26.
Ортом
вектора
называется вектор
,
который имеет единичную длину и то же
направление, что и вектор
.
(8.6)
Процесс получения орта вектора называется нормированием.
Если координаты
,
то координаты соответствующего вектору
орта, т.е. нормированного вектора,
. (8.7)
Направление вектора определяется углами α, β, γ, образованными вектором с осями координат Ox, Oy, Oz.
Определение 27.
Косинусы углов α, β, γ, образованных векторов с осями координат Ox, Oy, Oz, называются направляющими косинусами вектора и вычисляются по формулам:
,
,
. (8.8)
Тогда координаты нормированного вектора по (8.8) в V3 будут:
.
Направляющие
косинусы вектора связаны соотношением
.
Для V2:
с соотношением:
.
14. Ориентация пространства. Правая и левая тройки веторов
Рассмотрим двумерное векторное пространство V2. Выделим в нем два подпространства: положительно ориентированное (против часовой стрелки) и отрицательно ориентированное (по часовой стрелке). Подпространство, в котором выбрана положительная ориентация, назовем просто ориентированным.
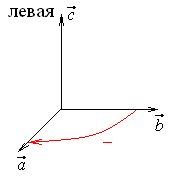
Рассмотрим трехмерное векторное пространство V3. По аналогии с ориентацией плоскости выделим в нем два подпространства: положительно ориентированное и отрицательно ориентированное. Положительно ориентированный в нем базис назовем правым, отрицательно ориентированный соответственно – левым.
Рассмотрим три
некомпланарных вектора
,
,
(порядок определен строго).
Определение 28.
Три
вектора
,
,
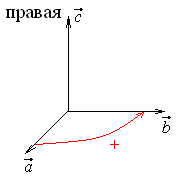
образуют правую
тройку,
если с конца третьего вектора кратчайший
поворот от первого вектора ко второму
совершается против часовой стрелки.
Примеры.
1)
,
,
2)
,
,
3)
,
,
15. Векторное произведение: определение, свойства
Определение 29.
Векторным
произведением
векторов
и
называется вектор
,
удовлетворяющий условиям:
1
)
;
(8.9)
2)
и
;
3)
,
,
– правая тройка.
Обозначается
или
.
Из определения
следует:
.
Вычислим векторные произведения ортов.
Покажем, что
.
1)
;
2)
и
;
3)
,
,
– правая тройка.
Покажите
самостоятельно, что
,
,
и т.д. Заполните таблицу:
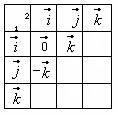
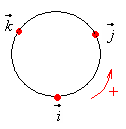
Эти произведения легко заполнить с помощью схемы Гамильтона (рис. справа).
Свойства векторного произведения
1.
Антикоммутативность:
=–
.
2. Ассоциативность относительно умножения на число:
.
3.
Два ненулевых вектора
и
коллинеарны тогда и только тогда, когда
их векторное произведение равно нулевому
вектору:
.
Следствие.
(см. также таблицу произведения ортов
).
4. Условие
коллинеарности двух векторов:
=
.
5. Дистрибутивность:
(справа),
(слева).