
Лекция № 8 МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ УПРАВЛЕНИЯ В БИОЛОГИИ
Теория управления имеет дело не с реальными объектами, а с их описаниями, называемыми моделями. Предполагается, что описание объекта (иногда говорят – системы) дается в виде некоторого количества стандартных элементов, связанных между собой. Заданную таким образом систему будем называть моделью реального объекта. При этом сама теория управления вовсе не занимается проблемой построения моделей; считается, что эта проблема лежит вне компетенции теории управления, хотя некоторые оценки степени соответствия модели объекту могут быть даны и в рамках теории управления. Действующие на объект внешние факторы принято называть входными воздействиями или входными сигналами (входами), а ее реакции − выходными сигналами (выходами).
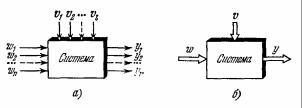
В биологических системах будем различать два типа входных сигналов – возмущающие и задающие. Задающие сигналы определяют некоторые требования, которые биологическая система должна выполнить. Остальные входные сигналы, в том числе определяющие условия, в которых функционирует система, относятся к возмущающим. На рис. 1 задающие входные сигналы обозначены через ω1 , ω2 , …, ωn , возмущающие – через
υ1 , υ2 , …, υl . Символами y1 , y2 , …, yr обозначены выходные переменные.
Одна и та же реально существующая величина в зависимости от желания исследователя и выбранного им способа описания системы может выступать в качестве различных сигналов в модели. Так, при исследовании системы кровообращения в организме часто в качестве выходной переменной выбирают артериальное давление. Величины, характеризующие другие системы организма и меняющиеся в процессе решения (например, величина легочной вентиляции), играют в этом случае роль возмущающих сигналов. Задающим входом в модели системы кровообращения, построенной в соответствии со схемой классического типа, является специальный опорный сигнал − уставка. При описании же реакций системы дыхания (на вдыхание углекислоты) легочная вентиляция играет уже роль выходного сигнала, входным сигналом является концентрация углекислоты во вдыхаемом воздухе. Если в ходе исследования меняются переменные в других системах (то же артериальное давление), то они будут выступать в качестве внешнего возмущающего сигнала.
Рисунок 1. Входные и выходные сигналы системы. а) ω1 , ω2 , …, ωn − задающие входы, υ1 , υ2 , …,
υl – возмущающие входы; y1 , y2 , …, yr − выходы; б) сигналы показаны обобщенно; ω, υ и y – векторы размерности n, l и r соответственно.
При описании биосистем с помощью математических моделей переменные и параметры биосистемы являются переменными и параметрами описывающих ее уравнений.
Современные способы изображения биологических систем в виде графических схем ведут свое происхождение, с одной стороны, от традиционных изобразительных методов, используемых в биохимии, физиологии и других биологических дисциплинах, и, с другой, от структурных схем, получивших в свое время широкое распространение для программирования аналоговых вычислительных машин.
1
Применяемые в настоящее время схемы во многом сохраняют точность и строгость, присущие схемам аналогового моделирования, но при этом не предназначены для узких целей исследования систем с помощью тех или иных вычислительных средств, а имеют общий смысл наглядного представления структурных свойств и особенностей исследуемых моделей.
Для получения схемы моделирования какого-либо процесса или системы требуется их математическое описание. Такое описание объектов часто дается в форме дифференциальных уравнений k-го порядка, разрешенных относительно старших производных, т. е.
|
|
d k x |
|
|
|
(1) |
|
|
|
i |
= fi (x1 |
, x1' , x1'' ,...,x1(k −1) ; xm , x'm , x''m ,..., xm(k −1) ; z), |
|
|
|
|
|
dzk |
|
|
|
||
|
i =1,2,...,m, |
|
|
|
|
||
где |
x – переменная системы (зависимая переменная), z – независимая переменная, |
x' |
, |
x'' , |
|||
|
i |
|
i |
|
i |
||
…, xi(k −1) − производные xi по z от первого до (k – 1)-го порядка.
Систему уравнений (1) всегда можно представить в виде системы уравнений первого порядка.
Для этого достаточно ввести новые переменные
yi0 |
= xi , |
|
|
|
|||
y |
i1 |
= |
dyi0 |
= x' |
, |
||
|
|
||||||
|
|
dz |
i |
(2) |
|||
|
|
|
|
|
|||
|
|
|
dyi1 |
'' |
|
||
y |
i2 |
= |
|
|
= x |
, |
|
|
|
||||||
|
|
dz |
i |
|
|||
|
|
|
|
|
|
||
.................................. |
|||||||
y |
|
|
= dyi,k −2 |
= x(k −1) . |
|||
|
i,k −1 |
|
|
dz |
|
i |
|
|
|
|
|
|
|
||
Тогда уравнения (1) принимают вид
dyi,k −1 |
= f |
i |
(y |
, y |
20 |
,..., y |
1,k −1 |
; y |
m0 |
, y |
m0 |
,..., y |
m,k −1 |
; z). |
(3) |
|
|
||||||||||||||
dz |
10 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вместе с системой уравнений (2) уравнение (3) и представляет собой систему, составленную из km уравнений первого порядка.
Поэтому всегда можно считать, что исследуемая система описывается уравнениями
вида
dxi |
= f (x , x |
|
,..., x |
|
; z), |
(4) |
dz |
|
|
||||
i 1 |
2 |
|
m |
|
||
|
|
|
|
i =1,2,...,m.
Если независимой переменной z является время t, то система дифференциальных уравнений (4), переписанная в виде
2
x = fi (x1 , x2 ,...,xm ;t ), |
(5) |
i =1,2,...,m, |
|
называется динамической системой.
Динамические системы описывают протекание физических, химических, биологических явлений и процессов во времени. Если уравнения приведены к виду (4) или (5), то говорят, что они представлены в так называемой нормальной форме Коши. Решение системы (5) при некоторых ограничениях на вид функций fi полностью определяется
значениями функций x1 , x2 , …, xm в некоторый момент времени t0 , которые называются
начальными условиями системы (5). Начальные условия обычно записываются следующим образом:
x1(t0 ) = x10 ,
x2 (t0 ) = x20 , |
(6) |
.....................
xm (t0 ) = xm0 .
Переменные x1 , x2 , …, xm в (5) называются иногда фазовыми координатами
системы. Задание совокупности фазовых координат определяет состояние системы в текущий момент времени.
Графические схемы, используемые для описания структуры системы, должны с той или иной степенью полноты отражать связи между ее фазовыми координатами.
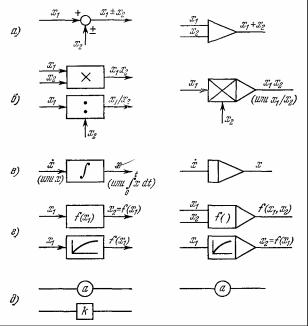
Рисунок 1. Символы, используемые в схемах моделирования. В левом столбце – обозначения наиболее часто используемые в схемах моделирования, в правой − обозначения, применяемые для программирования аналоговых вычислительных машин. а) суммирование (или вычитание); б) умножение (или деление), во втором случае на схеме желательно указывать делимое и делитель; в) интегрирующее звено; г) нелинейное преобразование; д) постоянные коэффициенты.
3
Схема моделирования является строгим графическим отражением уравнений системы. Символы, используемые для отдельных элементов, должны быть стандартизированы, а все элементы структуры должны иметь один и тот же уровень детализации. Обычно при построении схем моделирования исходят из описания систем в нормальной форме Коши и используют набор стандартных обозначений элементов, показанный на рис. 1. Схема моделирования строится следующим образом: каждой фазовой координате ставится в соответствие один интегрирующий элемент (интегратор), а затем с помощью стандартных символов графически изображаются связи между интеграторами согласно правым частям уравнений (5). В различных областях, где применяются схемы моделирования, формулируется ряд специфических требований, более жестко регламентирующих способы изображения систем. Мы этих требований придерживаться не будем. В наших схемах мы будем использовать, в основном, элементы, приведенные в первом столбце рис. 1, хотя будем применять обозначение интегратора в любой из двух возможных форм – в виде прямоугольника или в виде треугольника.
Пример. Изобразим блок-схему и схему моделирования для простой динамической системы. Возьмем описание элемента кровеносного сосуда в форме так называемого эластичного резервуара. Пусть переменная х описывает количество крови, находящееся в данном отрезке сосуда – резервуаре. Тогда
x =ω – y, |
(7) |
где ω и y – темп притока и темп оттока крови для данного резервуара, соответственно. Будем считать приток крови независимым внешним сигналом. Темп оттока прежде всего зависит от давления в резервуаре, которое определяется соотношением
Р = |
1 |
(х−а), |
(8) |
С |
|
||
|
|
|
где Р – давление в резервуаре, С – коэффициент, определяющий эластичность кровеносного сосуда (емкость), а – константа, так называемый ненапряженный объем резервуара, т. е. такой объем крови, который может содержаться в резервуаре без повышения давления Р. Тогда темп оттока равен
у = |
1 |
(P −b), |
(9) |
R |
|
||
|
|
|
где R – сопротивление сосуда току крови, b – константа, равная давлению в следующем резервуаре, куда оттекает кровь.
Система описывается тремя уравнениями (7) – (9). Чтобы привести описание системы к форме Коши, в нашем случае достаточно подставить выражения (8) и (9) в (7). Тогда получаем
x = ω− |
1 |
(x −a) + |
b |
. |
(10) |
RC |
|
|
|||
|
|
R |
|
||
Один из возможных вариантов блок-схемы и два варианта схем моделирования эластичного резервуара приведены на рис. 2.
4
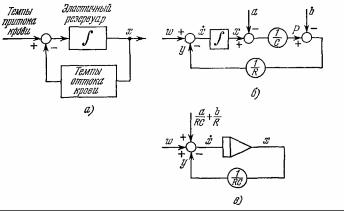
Рисунок 2. Примеры блок-схемы системы и схем моделирования. Изображение системы в виде блоксхемы позволяет использовать произвольные символы с разной степенью детализации (а). В схемах моделирования применяется изображение элементов только с помощью стандартных символов; на рис. б) и в) показаны два возможных варианта схем моделирования эластичного резервуара для системы кровообращения.
5
