5. Экспериментальное наблюдение петли гистерезиса

П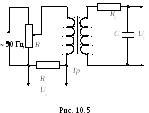ринципиальная схема установки представлена на рис. 10.5. На первичную обмотку трансформатора (Тр) подается переменное напряжение. В цепь первичной обмотки включен резистор с сопротивлением R₁. В сердечнике трансформатора из исследуемого ферромагнитного материала создается переменное магнитное поле, напряженность которого пропорциональна силе тока, идущего через сопротивление R₁. Следовательно, если с резистора R₁ подать напряжение на вход X усилителя осциллографа, то отклонение электронного луча на экране будет пропорционально напряженности Η магнитного поля.

Переменное магнитное поле в сердечнике трансформатора возбуждает в его вторичной обмотке ЭДС индукции, пропорциональную скорости изменения индукции В магнитного поля. Если на вход Υ усилителя осциллографа подать напряжение с конденсатора С, то оно будет пропорционально заряду на этом конденсаторе, который, в свою очередь, пропорционален В (при некоторых условиях, о которых будет сказано ниже). Таким образом, на горизонтальный и вертикальный входы осциллографа одновременно подаются напряжения, пропорциональные соответственно напряженности Η и индукции В магнитного поля. На экране осциллографа будет наблюдаться петля гистерезиса.

Если исследуемый образец выполнен в виде тороида, а первичная и вторичная обмотки трансформатора содержат Ν₁ и N₂ витков соответственно, то при радиусе витка обмотки r_в<<r_т (если толщина тороида гораздо меньше его среднего радиуса r_т) напряженность магнитного поля в тороиде равна

(10.13)

где r_T = (r₁ + r₂)/2, r₁ и r₂ — внутренний и наружный радиусы тороида, I₁ — сила тока в первичной обмотке трансформатора. Падение напряжения на сопротивлении R₁ равно

(10.14)

и пропорционально отклонению электронного луча по горизонтальной оси:

U_x = b_lx. (10.15)

С учетом (10.14) и (10.15) выражение для напряженности магнитного поля может быть записано в виде

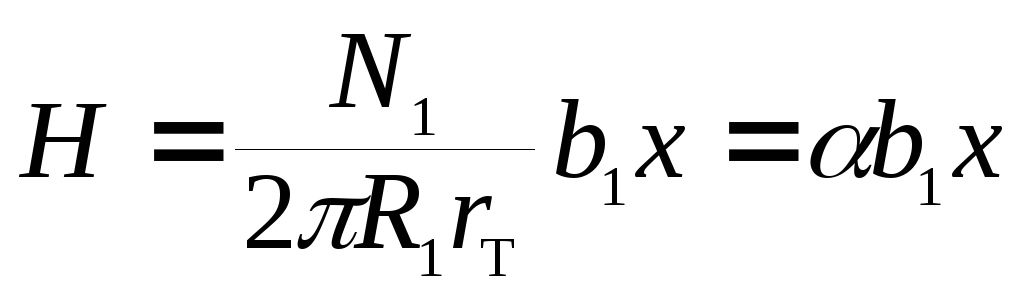, (10.16)

где

. (10.17)

По закону Фарадея ЭДС индукции во вторичной обмотке равна

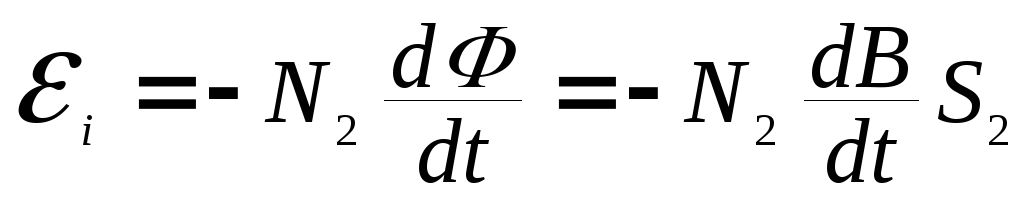, (10.18)

где Φ — поток вектора магнитной индукции В сквозь один виток вторичной обмотки,

, (10.19)

S - площадь поперечного сечения тороида (а — толщина тороида).

По закону Ома для вторичной обмотки трансформатора имеем

, (10.20)

где U_c - напряжение на конденсаторе, - сила тока во вторичной обмотке, - ее индуктивность. Если электроемкость С и сопротивление R₂ достаточно велики, то

, (10.21)

где q — заряд на обкладках конденсатора.

С учетом (10.21) выражение (10.20) можно переписать:

. (10.22)

Напряжение на конденсаторе U_c равно напряжению U_y, подаваемому на вертикальный усилитель осциллографа:

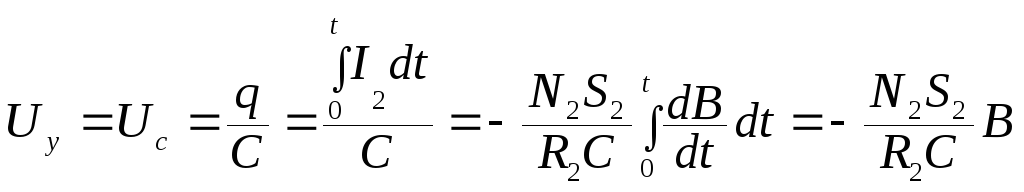. (10.23)

Это напряжение пропорционально отклонению электронного луча по вертикальной оси:

. (10.24)

Из выражений (10.23) и (10.22) получаем (опуская знак минус) индукцию магнитного поля:

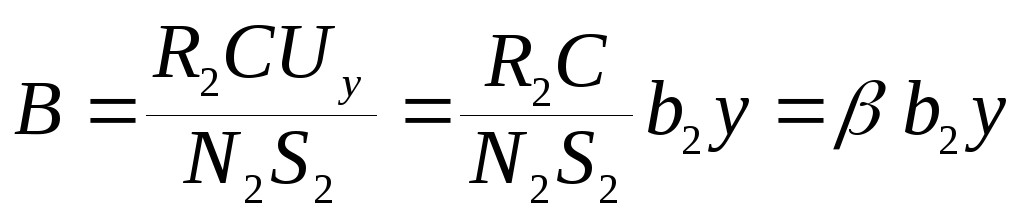, (10.25)

где 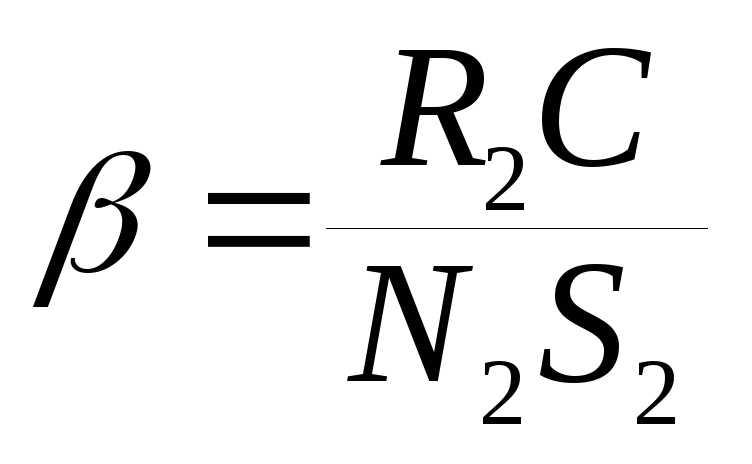. (10.26)

Изменяя силу тока I₁ в первичной обмотке трансформатора, можно наблюдать изменение петли гистерезиса на экране осциллографа.

По площади петли гистерезиса можно найти работу перемагничивания ферромагнетика, отнесенную к единице объема ферромагнитного образца. Объемная плотность энергии магнитного поля равна

. (10.27)

Элементарная работа, совершаемая в цикле перемагничивания, равна

A_п = dw_B = HdB. (10.28)

Работа за полный цикл перемагничивания

. (10.29)

С учетом (10.24) и (10.29) получаем

, (10.30)

где — площадь петли гистерезиса на экране осциллографа. Следует иметь в виду, что эта площадь измерена в делениях шкалы осциллографа.