2.2. Простейшие движения твердого тела

К простейшим движениям твердого тела относятся поступательное и вращательное.

Поступательным называется движение твердого тела, при котором любая прямая, взятая в теле, остается параллельной своему начальному положению.

Теорема. При поступательном движении все точки твердого тела описывают одинаковые траектории и имеют в каждый момент времени равные скорости и ускорения.

Вращательным называется движение твердого тела, при котором все точки некоторой прямой, связанной с телом, остаются неподвижными во время движения. Эта прямая называется осью вращения.

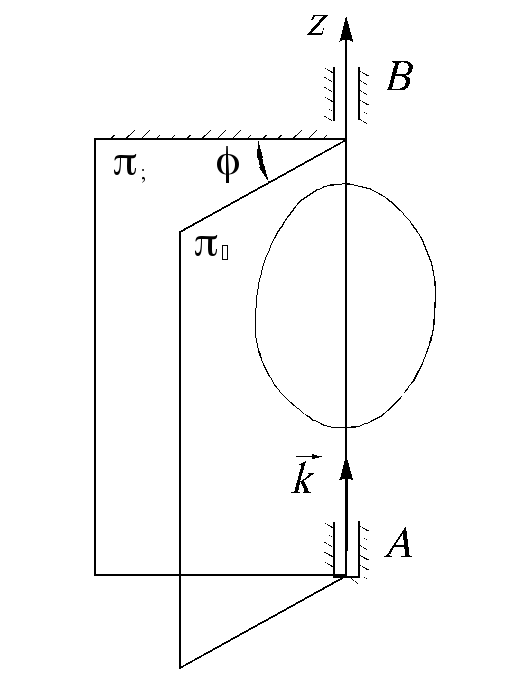
Рис. 2.2.1

Положение тела определено, если задан угол между плоскостями и , проходящими через ось вращения ( с единичным направляющим вектором ). (рис. 2.2.1). Плоскость неподвижна, а плоскость жестко связана с телом. Угол измеряется в радианах и изменяется с течением времени, – уравнение вращательного движения твердого тела.

Угловая скорость характеризует изменение угла поворота с течением времени.

Угловое ускорение – характеризует быстроту изменения угловой скорости.

Если угловая скорость постоянна, то вращение называется равномерным и происходит по закону .

Если угловое ускорение постоянно, то вращение называется равнопеременным и происходит согласно уравнениям:

, .

Модули скорости, ускорения, касательного, нормального ускорений точки вращающегося тела, находящейся на расстоянии от оси вращения, определяются по формулам:

, , , ,

Ускорение точки составляет угол с направлением нормали, при этом

.

Пример 2.2.1. Маховое колесо радиуса начинает вращаться равноускоренно из состояния покоя. Через 10 мин после начала движения оно имеет угловую скорость, равную . Определить угловое ускорение колеса; скорость и ускорение точки на ободе колеса и число оборотов через 10 мин после начала вращения.

Решение:

1. Колесо вращается равноускоренно, т.е. его угловое ускорение ε постоянно. При этом угловая скорость и угол поворота колеса изменяются по законам:

где , т.к. движение начинается из состояния покоя.

Подставляя и , находим

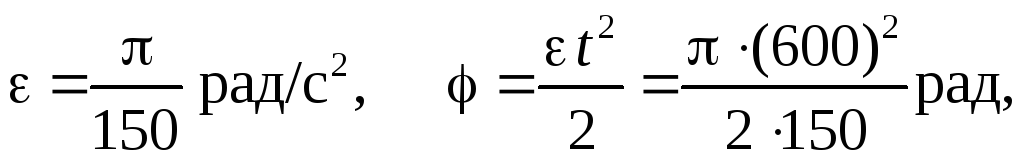
причем , где N – число оборотов колеса. Тогда оборотов.

2. Скорость точки на ободе колеса определяется по формуле и равна м/с. Скорость направлена по касательной к окружности радиуса R, т.е. перпендикулярно радиусу ОМ.

3. Ускорение точки на ободе колеса складывается из касательного и нормального ускорений: . Значения касательного и нормального ускорений соответственно равны: . Модуль ускорения точки равен Векторы скорости и ускорения точки показаны на рисунке 2.2.2.

Подставляя числовые значения, находим:

a_τ = 0,628 см/с², a_n = 47,37 м/с², a = 47,4 м/с².

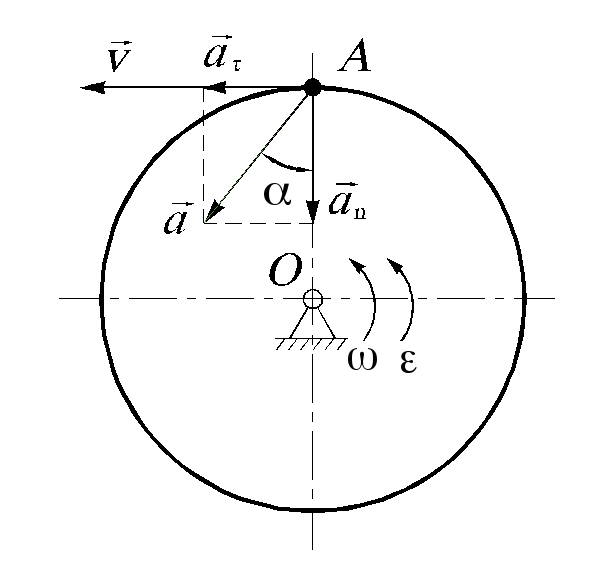
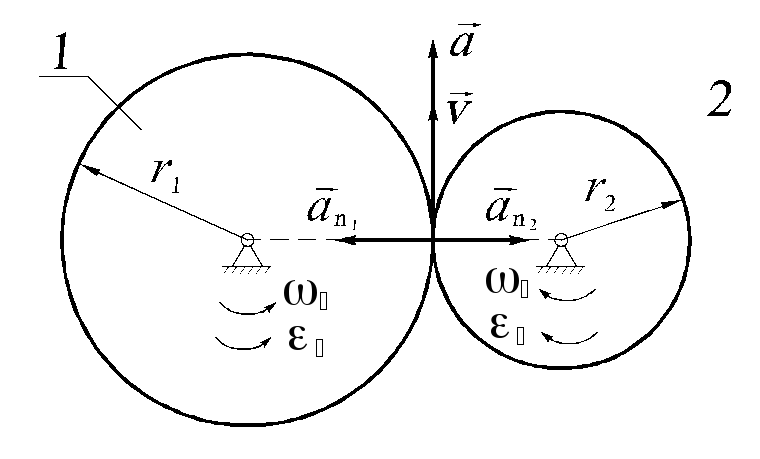
рис. 2.2.2 рис. 2.2.3 рис. 2.2.4

Пример 2.2.2. Зубчатые колеса 1 и 2 радиусов r₁ и r₂, соответственно, находятся во внешнем зацеплении (рис. 2.2.3). Колесо 1 имеет в данный момент угловую скорость ω₁ и угловое ускорение ε₁. Найти угловую скорость и угловое ускорение колеса 2, а также касательные и нормальные ускорения находящихся в соприкосновении точек колес.

Решение:

1. Скорости точек соприкосновения колес, находящихся в зацеплении, равны, т.е.

,

откуда

в любой момент времени.

2. Найдем угловое ускорение колеса 2:

Отсюда следует, что угловые ускорения колес связаны такой же зависимостью, как и угловые скорости, а касательные ускорения точек соприкосновения колес равны между собой:

Нормальные ускорения точек соприкосновения колес определяются формулами .

Направления векторов , , , показаны на рисунке 2.2.4.

Задача 2.2.1. Диск радиуса 2 м вращается равномерно вокруг неподвижной оси, проходящей перпендикулярно плоскости диска через его центр, с угловой скоростью, соответствующей 300 об/мин. Найти угловую скорость и угловое ускорение диска, а также скорость и ускорение точки, расположенной на ободе диска.

Ответ: ω = 31,4 рад/с, ε = 62,8 рад/с, v = 62,8 м/с, a = 1973 м/с².

Задача 2.2.2. Тело, вращающееся равноускоренно из состояния покоя, сделало за секунд N оборотов. Найти угловое ускорение тела.

Ответ: .

Задача 2.2.3. Колесо, сделав N оборотов, остановилось через t секунд после начала движения. Предполагая, что вращение равнозамедленное, найти начальную угловую скорость колеса.

Ответ: .

Задача 2.2.4. В момент выключения двигателя ротор вращался с угловой скоростью 20 рад/c. Через сколько секунд двигатель остановится, если ротор вращается равнозамедленно с угловым ускорением 20 рад/c². Сколько оборотов сделает ротор до остановки?

Ответ: t = 10 с, N = 500 об.

Задача 2.2.5. В ременной передаче шкив диаметра  мм начинает вращаться из состояния покоя с постоянный угловым ускорением 0,1 рад/c², приводя во вращение шкив диаметра  мм. Через какое время после пуска шкив диаметра будет обладать угловой скоростью, соответствующей 200 об/мин?

Ответ: 40 с.

Задача 2.2.6. Тело вращается вокруг неподвижной оси. В некоторый момент времени ускорение точки, расположенной на расстоянии 0,5 м от оси вращения, равно 4 м/c² и составляет с радиусом угол 60°. Найти в этот момент времени угловую скорость и угловое ускорение тела, а также скорость, касательное и нормальное ускорения точки, расположенной на расстоянии 1,5 м от оси вращения.

Ответ: ω = 2 рад/с, ε = 6,93 рад/с, v = 3 м/с, a = 10,4 м/с².

Задача 2.2.7. Грузы 1 и 2 (рис. 2.2.5) прикреплены к тросам, намотанным на ступенчатый барабан с радиусами ступеней  м,  м. Груз 1 опускается с постоянным ускорением  м/с² и имеет в данный момент времени скорость  м/с. Определить в этот же момент времени угловые скорость и ускорение барабана, скорость и ускорение груза 2 и точки А барабана.

Ответ: , v₂ = v_A = 2 м/с, a₂ = 1 м/с², a_A = 20,02 м/с².

Задача 2.2.8. Диск вращается равноускоренно из состояния покоя. В тот момент, когда угловая скорость диска равна 4 рад/с, ускорение точки, находящейся от оси вращения на расстоянии 1 м, равно 20 м/с². Найти ускорение точки, находящейся на расстоянии 1,5 м от оси вращения, в момент времени 0,5 с.

Ответ: а = 56,92 м/с².

рис. 2.2.5 рис. 2.2.6 рис. 2.2.7

Задача 2.2.8. Зубчатое колесо 1 радиуса 0,8 м вращается согласно закону рад и находится в зацеплении с колесом 2 радиуса 0,5 м (рис. 2.2.6). Определить угловые скорости колес в момент времени ( – в секундах), число оборотов, совершенных колесом 2 за это время.

Ответ: : ω₁ = 62,8 рад/с, ω₂ = 100,5 рад/с, N = 16 об.

Задача 2.2.9. В зубчатой передаче движение от ведущего колеса 1 радиуса 0,2 м через блок колес 2 передается колесу 3 радиуса 0,8 м (рис. 2.2.7). Определить угловую скорость колеса 3 в момент времени 2 с, если колесо 1 вращается согласно закону , .

Ответ: рад/с.

Задача 2.2.10. Редуктор (рис. 2.2.8) состоит из четырех зубчатых колес, жестко закрепленных на валах. Вал I вращается с угловой скоростью  рад/с. Определить угловую скорость вала II, если число зубьев на соответствующих колесах .

Ответ: .

Задача 2.2.11. Двухступенчатый редуктор (рис. 2.2.9) состоит из конической и цилиндрической зубчатых передач с числом зубьев колес , , , . Вал I вращается с угловой скоростью  рад/с. Все зубчатые колеса жестко закреплены на валах. Определить угловую скорость вала II.

Ответ: рад/с.

рис. 2.2.8 рис. 2.2.9 рис. 2.2.10

Задача 2.2.12. Угловая скорость зубчатого колеса 1 изменяется по закону (рис. 2.2.10). Колесо 1 находится во внешнем зацеплении с зубчатым колесом 2, жестко соединенным с валом. На вал намотана нить, несущая груз 3. Определить скорость и ускорение груза в момент времени t = 1 с, если радиусы колес и вала соответственно равны:  м,  м,  м.

Ответ: , , груз движется вверх замедленно.

Задача 2.2.13. Механизм состоит из зубчатой рейки 1, блока зубчатых колес 2, зубчатого колеса 3 со шкивом 4, ступенчатого шкива 5 и груза 6 (рис. 2.2.11). Груз опускается по закону ( – в сантиметрах, – в секундах). В момент времени t = 2 с определить скорости и ускорения точек А, В и С, а также скорость и ускорение рейки, если  см,  см,  см,  см,  см,  см,

Ответ: v₁ = v_A = 80 см/с, a₁ = 40 см/с², a_A = 1600,5 см/с², v_B = 40 см/с, a_B = 201 см/с², v_C = 30 см/с, a_C = 61,8 см/с².

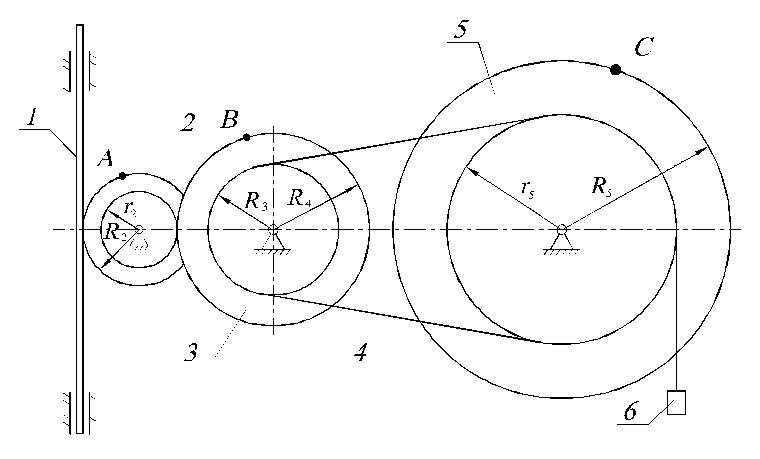
рис. 2.2.11 рис. 2.2.12

Задача 2.2.14. Механизм состоит из зубчатой рейки 1, зубчатых колес 2, 4, 6 со шкивами 3, 5, 7 и груза 8 (рис. 2.2.12). Рейка движется вверх ускоренно и в данный момент времени имеет скорость v₁ = 12 м/с и ускорение . В этот же момент времени определить скорости и ускорения точек А, В и С, а также скорость и ускорение груза, если  см,  см,  см,  см,  см,

Ответ: v_A = 6 см/с, a_A = 2,69 см/с², v_B = 9 см/с, a_B = 3,13 см/с², v_C = v₈ = 4 см/с, a_C = 1,55 см/с², a₈ = 1,33 см/с².

Задача 2.2.15. Твердое тело, вращающееся вокруг неподвижной оси, имеет в начальный момент времени угловую скорость . Известно, что во все время движения ускорение любой точки образует постоянный угол 45° с радиусом вращения. Найти зависимости угловой скорости и углового ускорения от времени.

Ответ: .
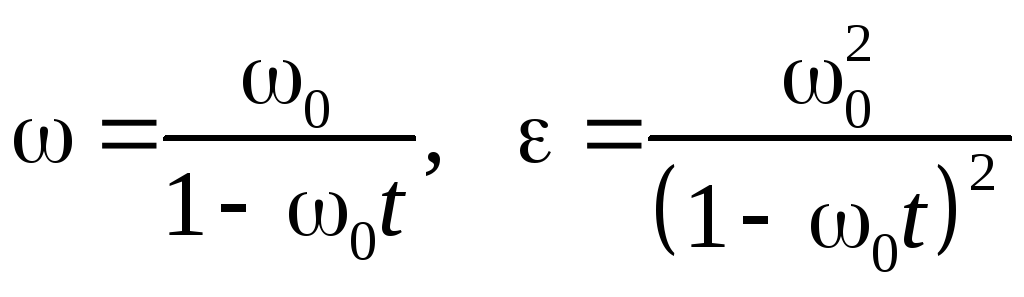