1.3. Равновесие при наличии трения

При стремлении сдвинуть тело, лежащее на шероховатой поверхности, возникает сила реакции, которая имеет две составляющие – нормальную и силу трения скольжения. Сила трения скольжения при равновесии тела меняется от нуля до максимального значения, которое определяется равенством

,

где f − коэффициент трения скольжения, N − нормальная реакция шероховатой поверхности.

Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого. Возникающий при этом момент сопротивления изменяется от нуля до максимального значения, которое определяется равенством

,

где δ − коэффициент трения качения.

Пример 1.3.1. Однородный тяжелый стержень опирается в точке А на шероховатый пол, а в точке В на гладкую стену (рис. 1.3.1). Определить угол a, который стрежень образует с горизонталью при равновесии, если коэффициент трения между полом и стержнем равен f.

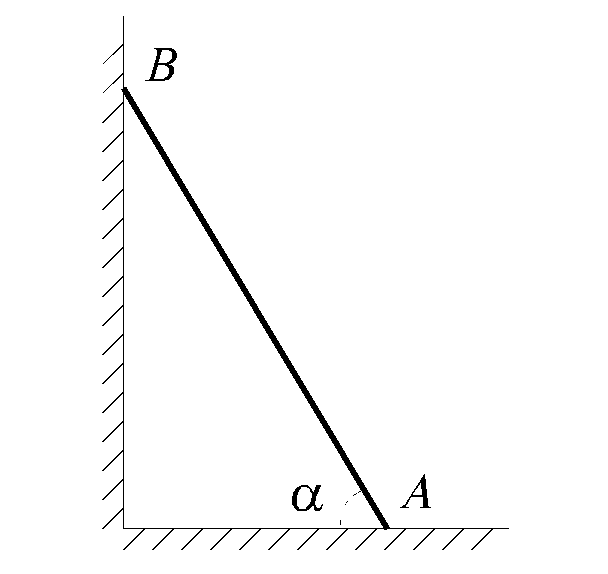
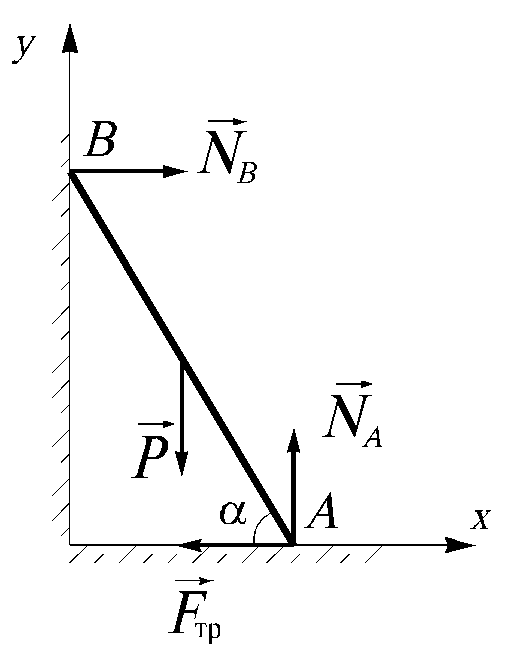
Рис.1.3.1 Рис.1.3.2

Решение:

1. Рассмотрим равновесие стержня, мысленно освобождая его от связей (стены в точке А и пола в точке В).

2. Изобразим силу тяжести и реакции связей (рис. 1.3.2).

3. Используя условия равновесия балки в форме

, , ,

имеем

, ,

, ,

, .

Откуда

, .

4. Запишем неравенство, которому удовлетворяет сила трения при равновесии

, или .

Откуда

.

Пример 1.3.2. Однородный цилиндр радиуса R покоится на шероховатой плоскости, образующей угол a с горизонтом (рис. 1.3.3). Определить, при каких значениях угла a возможно равновесие цилиндра, если коэффициент трения между цилиндром и плоскостью равен f, коэффициент трения качения равен δ.

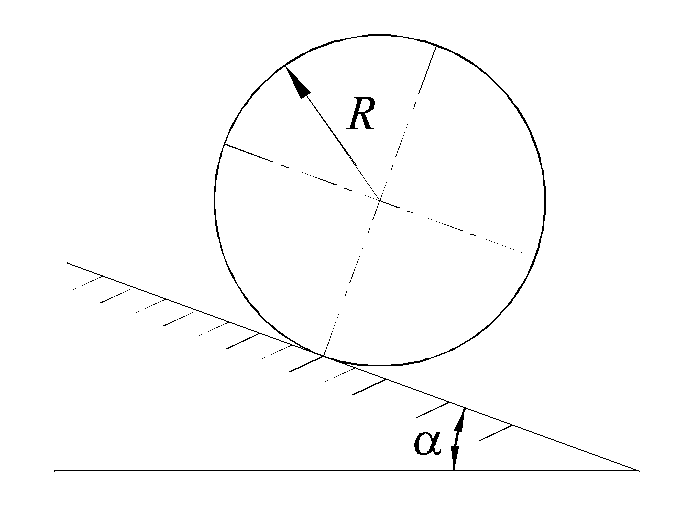
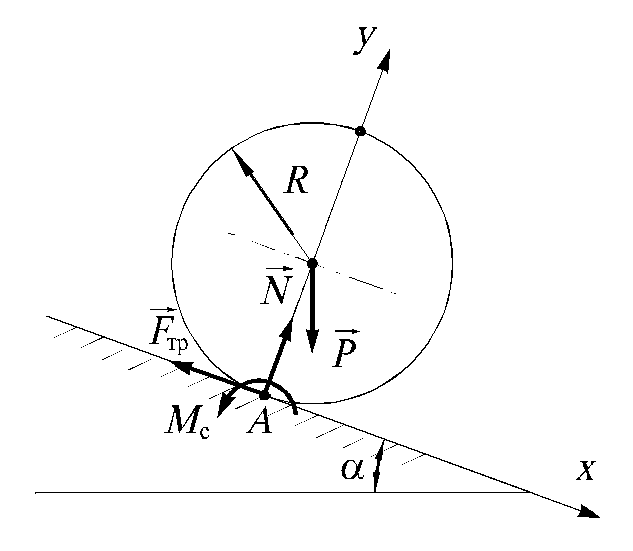
Рис.1.3.3 Рис.1.3.4

Решение:

1. Рассмотрим равновесие цилиндра, мысленно освобождая его от связи – шероховатой плоскости.

2. Изобразим силу тяжести и реакции связей (рис. 1.3.4).

3. Используя условия равновесия балки в форме

, , ,

имеем

, ,

, ,

, .

Откуда

, , .

4. Запишем неравенства, которым удовлетворяют сила трения и момент сопротивления качению при равновесии

и .

Откуда

, .

Цилиндр будет покоиться на шероховатой плоскости, если угол a удовлетворяет этим неравенствам.

Задача 1.3.1. На прямолинейный стержень длины 2l, нижний конец которого шарнирно закреплен, а средней точкой он опирается на ступеньку высоты h, надето тяжелое колечко. При каком значении коэффициента трения скольжения f колечко останется в равновесии, если <?

Ответ: 0.

Задача 1.3.2. Однородный куб массы m находится в равновесии (рис. 1.3.5). При каком значении силы Q, груз начнет подниматься вверх по наклонной плоскости, если коэффициент трения скольжения равен f?

Ответ: .

Задача 1.3.3. Однородный прямолинейный стержень веса P длины 2l опирается концами на стенки прямоугольного канала с вертикальной осью симметрии (рис 1.3.6). На каком расстоянии от центра тяжести стержня допустимо поместить груз веса Q, чтобы стержень оставался в равновесии в горизонтальном положении, если коэффициент трения скольжения между стержнем и стенками канала равен f?

Ответ: .

Рис.1.3.5 Рис.1.3.6 Рис.1.3.7

Задача 1.3.4. Однородный брус веса P опирается в точке A на гладкую стену, а в точке B под углом на негладкий пол (рис. 1.3.7). В точках A и B на брус действуют силы и . При каких значениях коэффициента трения скольжения между полом и стержнем положение стержня не изменится?

Ответ: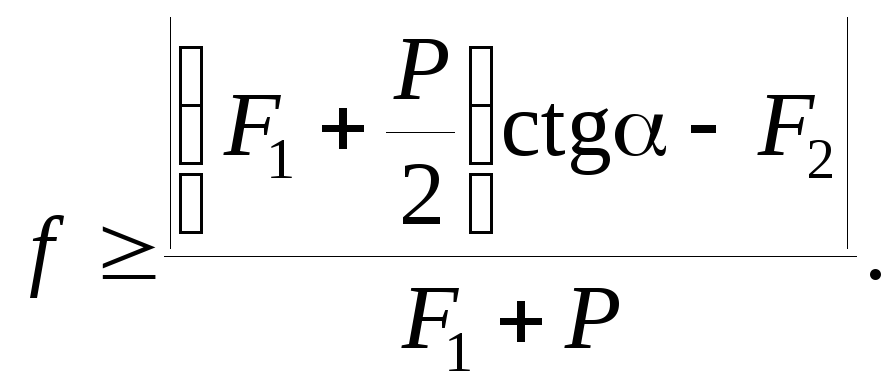

Задача 1.3.5. На шероховатой поверхности, профиль которой моделируется уравнением , расположена тяжелая материальная точка. Определить минимальное расстояние от точки до оси абсцисс при ее равновесии, если коэффициент трения скольжения равен f.

Ответ:

Задача 1.3.6. Материальная точка массы m, прикрепленная к концу эластичного шнура с коэффициентом жесткости c, расположена на шероховатой горизонтальной плоскости. Другой конец шнура закреплен в неподвижной точке этой же плоскости. При каких значениях коэффициента трения диаметр области равновесия точки будет равен d, если длина недеформированного шнура равна l₀?

Ответ:

Задача 1.3.7. Однородный брус 1 длины l удерживается при помощи нерастяжимой нити, перекинутой через неподвижный блок 3, к концу которой прикреплен груз 2 одинаковой с брусом массы (рис 1.3.8). Наклонная плоскость имеет шероховатый участок длины a. Определить минимальное значение коэффициента трения , при котором система будет находиться в равновесии.

Ответ:.

Задача 1.3.8. Однородный прямолинейный стержень массы m расположен на шероховатой горизонтальной плоскости и шарнирно закреплен в точке, отстоящей от концов стержня на расстоянии a и b соответственно. Определить минимальное значение момента пары сил, которая может вывести стрежень из состояния равновесия, если коэффициент трения скольжения равен .

Ответ:

Задача 1.3.9. Конструкция из двух однородных стержней длины 1 м, соединенных в виде тавра, массы 10 кг расположена на шероховатой горизонтальной плоскости и шарнирно закреплена в своем центре масс. Определить минимальное значение момента пары сил, которая может вывести конструкцию из состояния равновесия, если коэффициент трения скольжения равен 0,2.

Ответ: = 3,8 Н·м.

Задача 1.3.10. Кривошипно-ползунный механизм (рис. 1.3.9), расположенный в вертикальной плоскости, состоит из одинаковых однородных стержней 1, 2 длины l и веса P, а также ползуна 3 такого же веса. Определить, при каких значениях угла a механизм будет находиться в равновесии, если коэффициент трения между ползуном и горизонтальной плоскостью равен f.

Ответ: .

Рис.1.3.8 Рис.1.3.9 Рис.1.3.10

Задача 1.3.11. Однородный брус длины l веса P, расположенный на гладкой горизонтальной плоскости, втягивается в горизонтальную шероховатую трубу горизонтальной силой F. Установить закон изменения модуля силы F при равномерном движении бруса внутри трубы.

Ответ: =, где – длина части бруса, находящейся внутри трубы.

Задача 1.3.12. Ступенчатое колесо , касаясь вертикальной шероховатой стены, удерживается в равновесии при помощи нерастяжимой нити (рис. 1.3.10). Определить наименьшее значение коэффициента трения между колесом и стеной, при котором возможно равновесие, если центр тяжести колеса совпадает с его геометрическим центром симметрии.

Ответ: .

Задача 1.3.13. Однородный цилиндр 1 радиуса R (рис. 1.3.11) вращается под действием пары сил с моментом M. Определить наименьшее значение силы F, приложенной к рычагу 2 колодочного тормоза, способной остановить цилиндр, если коэффициент трения между тормозной колодкой 3 и цилиндром равен f. Весом рычага и тормозной колодки пренебречь.

Ответ: .

Задача 1.3.14. Однородный каток 2 соединен при помощи нерастяжимой нити, перекинутой через неподвижный блок, с грузом 1 веса (рис 1.3.12). При каком минимальном значении веса катка система будет находиться в равновесии, если коэффициент трения между грузом и плоскостью равен f, коэффициентом трения качения равен δ и <?

Ответ: .

Рис.1.3.11 Рис.1.3.12 Рис.1.3.13

Задача 1.3.15. Подъемный механизм (рис. 1.3.13), состоящий из барабана 1 радиуса R, системы неподвижных блоков и нерастяжимого троса, осуществляет равномерный подъем груза 2 массы m. Определить момент M пары сил, приложенной к барабану, если коэффициент трения между грузом и плоскостью равен f.

Ответ: .

Задача 1.3.16. Лестница, состоящая из двух одинаковых однородных частей 1 и 2, соединенных между собой цилиндрическим шарниром, стоит на шероховатом полу (рис. 1.3.14). Определить наибольший угол между частями лестницы при равновесии, если коэффициент трения между лестницей и полом равен f. Трением в шарнире пренебречь.

Ответ:

Рис.1.3.14 Рис.1.3.15

Задача 1.3.17. Три одинаковых трубы радиуса r (рис. 1.3.15) находятся в равновесии из-за возникающих в точках контакта сил трения. Определить максимальное расстояние между центрами труб и минимальный коэффициент трения между трубами и полом, если коэффициент трения между трубами равен f.

Ответ: ; =.