
- •Введение
- •3.2Измерители механических величин
- •В позиционных и следящих системах
- •3.3 Измерители рассогласования
- •Позиционных и следящих систем.
- •1.4. Диодная схема переключения каналов грубого и точного отсчетов
- •1.2. Измерители скорости вращения
- •2.1. Выбор рода тока и типа двигателя
- •2.2. Выбор номинальной скорости и мощности двигателя
- •2.3. Выбор передаточного отношения редуктора
- •2.4. Безредукторный позиционный и следящий приводы
- •3.1. Эволюция преобразователей в системах электропривода
- •3.2.2. Системы шип - двигатель
- •3.3.2. Преобразователи
2.2. Выбор номинальной скорости и мощности двигателя
Выбор номинальной скорости двигателя должен подчиняться двум требованиям - обеспечению лучших динамических свойств системы, т. е. уменьшению длительности переходных процессов, и улучшению точностных показателей за счет снижения погрешности, вносимых редуктором.
Упрощенное выражение для длительности переходных процессов при постоянном моменте на валу двигателя [16] имеет вид

где Jд и Jмех - момент инерции двигателя и рабочей машины, каждый относительно своей оси; δ - коэффициент, учитывающий момент инерции элементов механической передачи, расположенных на оси двигателя; λм- перегрузочная способность двигателя по моменту; знак "минус" в этом выражении относится к пуску, "плюс" - к торможению. Из него следует, что целесообразно иметь двигатель, во вращающихся элементах которого запасается минимум кинетической энергии (Jдδωд2 = min). Это следует из того, что все элементы формулы, кроме первого члена числителя, неизменны. Величина Jмех ω2мех определяет запас кинетической энергии в механизме; Mмехωмех - представляет мощность, необходимую для преодоления статического момента при заданной скорости механизма; Мд. ном ωд - мощность двигателя, которая определяется нагрузочной диаграммой привода и, следовательно, тоже является определенной.
Из формулы (2.2) следует, что если редуктор спроектирован и его передаточное отношение задано, то единственным средством сокращения длительности переходных процессов является выбор двигателя для заданной мощности и скорости ωд — jωмех с минимальным моментом инерции. Для этого надо использовать предназначенную для динамических режимов серию двигателей со специальной геометрией - с удлиненной формой ротора и малым диаметром. Внутри этой серии, как было показано выше, следует выбирать двигатели, в обозначения типоразмеров которых входит буква L. Двигатели, имеющие индексы М (средняя длина) и тем более S (короткие), использовать не следует.
Нормально при проектировании электромеханической установки для обеспечения наибольшей производительности следует выбирать как скорость двигателя, так и передаточное отношение редуктора. Как показывает анализ, у двигателей неизменной мощности момент инерции с ростом скорости падает. Однако запас кинетической энергии, напротив, снижается при уменьшении скорости (рис. 2.6). Следует иметь в виду, что у некоторых типов двигателей (например, у двигателей постоянного тока 4П) запас кинетической энергии при некоторой скорости (около 1000 об/мин) проходит через минимум.
Указанные обстоятельства могут служить дополнительным доводом о целесообразности использования следящих систем с частотным управлением асинхронными двигателями. При этом могут быть применены двигатели с большим числом полюсов (например, с 2р = 6, вместо 2р = 4). В случае необходимости расширение диапазона регулирования скорости может быть достигнуто за счет использования частоты питающего напряжения, превышающего номинальное значение 50 Гц. Роторы коротко-замкнутых двигателей с числом полюсов от 2 до 8 конструируются на единой основе и соответственно могут использоваться при работе со скоростями до 3000 об/мин. Однако ограничением в этом случае служит необходимость пропорционального увеличения напряжения, ограничиваемого изоляцией обмотки статора, которая рассчитывается на напряжение 500 В. Следовательно, реально возможно увеличение частоты не более, чем на 30%. В машинах постоянного тока подъем напряжения в цепи якоря и соответственное увеличение скорости вращения свыше номинальных значений обычно недопустимы.

Рис.
2.6. Зависимости запаса кинетической
энергии в роторе двигателя серии
4П от номинальной частоты вращения
двигателя
В соответствии с изложенным в общем случае для повышения быстродействия привода целесообразно использовать низкоскоростные, так называемые высокомоментные двигатели. Такие двигатели в настоящее время нашли широкое применение в приводах подач металлорежущих станков. При этом одновременно упрощается редуктор и часто двигатель непосредственно сочленяется с ходовым винтом. В итоге погрешности, обусловленные неточностями механической передачи, практически устраняются.
Высокомоментные двигатели, как правило, изготавливаются с магнитоэлектрическим возбуждением. При этом оказывается возможным использование большого числа полюсов. Многополюсное исполнение обеспечивает большую равномерность вращения, что дополнительно уменьшает погрешность. Достоинством высокомоментных двигателей является также их высокая перегрузочная способность.
Следует, однако, иметь в виду, что габариты низкоскоростных высокомоментных двигателей существенно больше. Как известно, в первом приближении зависимость мощности двигателя от его габаритов определяется формулой
Р = сD2 lω, (2.3)
где D - диаметр ротора; l - активная длина ротора; ω- номинальная скорость; с - коэффициент, определяемый конструктивными особенностями данной серии двигателей. Следовательно, с уменьшением скорости масса двигателя, которая пропорциональна произведению D2l, возрастает обратно пропорционально скорости (рис. 2.7), а линейные размеры двигателя заданной мощности, полагая D ≈ l, изменяются обратно пропорционально скорости, возведенной в степень 1/3. В связи с этим тихоходные высокомоментные двигатели могут использоваться лишь при возможности беспрепятственного их размещения на каком-либо основании. Если же двигатель сам перемещается вместе с каким-либо элементом механизма, как, например, в роботах антропоморфной структуры, то применение их недопустимо. В этом случае, напротив, следует ориентироваться на быстроходные, двигатели (nном = 6000÷9000 об/мин) с использованием редуктора. Увеличение передаточного отношения редуктора за счет первых высокоскоростных звеньев оказывает несущественное влияние на габариты. Также в сервоприводах и следящих системах, используемых на самолетах, следует ориентироваться на высокоскоростные двигатели, так как увеличение подъемного веса приводит к существенным экономическим затратам. Однако при этом надо учитывать, что применение высокоскоростных двигателей требует увеличения передаточного отношения механического редуктора, работа которого при низких температурах и малом атмосферном давлении может нарушиться.
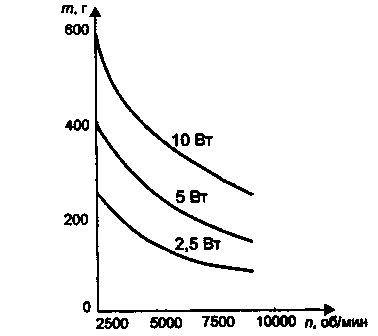
Рис. 2.7. Графики зависимости массы двигателя серии ДПР от номинальной
частоты вращения двигателя
Выбор мощности двигателя для позиционной и особенно для следящей системы является достаточно сложной и часто неопределенной задачей. Если программа работы позиционной системы может быть задана, то для расчета мощности двигателя с успехом применим метод средних потерь. Однако входные воздействия и процессы в следящей системе часто носят случайный характер. Соответственно нагрузочную диаграмму, т. е. зависимость Мд = ƒ(t) или I=ƒ(t) построить не представляется возможным; поэтому мощность двигателя приходится выбирать ориентировочно, пользуясь косвенными данными. Весьма часто необходимая мощность оценивается по максимальному моменту, ожидаемому в процессе работы привода. Тогда
![]()
где λM- перегрузочная способность двигателей той серии, которая признана наиболее целесообразной для использования в проектируемом приводе. Далее по величине Мд. ном нетрудно по каталогу выбрать двигатель для принятой ранее скорости. Естественно, что рассматриваемый путь дает ориентировочные результаты. Поэтому при изготовлении опытного образца установки приходится корректировать принятое решение.
Более обоснованно из условия нагрева обмотки можно выбрать двигатель, если имеется хотя бы ориентировочная возможность представить процесс работы привода, например предположить, что известен статический момент на валу механизма, причем постоянный, и что двигатель непрерывно находится в динамических режимах с ускорением на оси механизма ζм.
Тогда необходимый момент двигателя будет
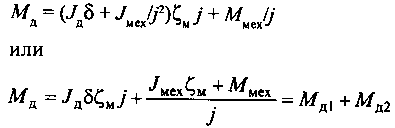
Здесь Мд1 =JДδζМj -составляющая момента, расходуемая на ускорение ротора двигателя; Мд2 = (Jмехζм + Mмех)/j - составляющая момента, передаваемая через редуктор на вал механизма; ζм -ускорение на валу механизма; j - передаточное отношение редуктора; δ - коэффициент, учитывающий наличие дополнительных инерционных масс на оси двигателя: муфты, тормозного диска и т. п
Определим передаточное отношение редуктора, обеспечивающее минимальный момент двигателя. Для этого возьмем производную от Мд по j и приравняем ее нулю:
Тогда
получим
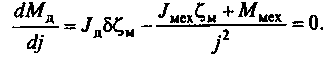

(2.5)
При использовании этого передаточного отношения согласно (2.4) будем иметь

Следовательно,
при оптимальном передаточном отношении
редуктора получим
и соответственно необходимый момент и мощность двигателя согласно (2.4) будут определяться выражениями
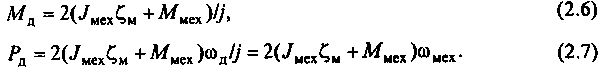
Как известно, обычно не представляется возможным расчетным путем оценить необходимую в электромеханической системе мощность двигателя. Приходится ориентировочно выбирать двигатель, а затем, используя его нагрузочную диаграмму, которая может быть построена на основе решения задач динамики, проверять пригодность этого двигателя по условиям нагрева. Как уже отмечалось, такой путь для выбора двигателя следящей системы практически нереален. Однако, если предположить, что скорость и ускорение изменяются по гармоническому закону, то подобный расчет возможен. В этом случае момент двигателя будет изменяться согласно равенству
![]()
Здесь статический момент положен постоянным.
Среднеквадратическое значение момента двигателя может быть подсчитано по формуле

В начале и конце периода, т. е. при t = 0 и t - 1, имеем sin 2νt = 0, cos νt= 1.
Следовательно,
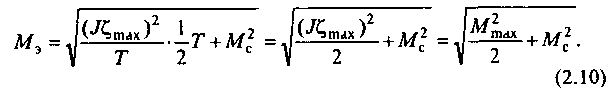
Таким образом, чтобы двигатель удовлетворял требованиям по условиям нагрева, должно быть

Здесь Ммах - амплитуда динамического момента.
К рассмотренному режиму может быть отнесен достаточно часто встречающийся случай, когда в техническом задании указаны предельные (т. е. амплитудные) значения скорости Ωмах и ускорения ζмах. При этом будем иметь

Следовательно, можно представить, что в проектируемой системе имеет место работа по гармоническому закону с частотой
ν = ζмах/Ωмах (2.13)
Соответственно может быть использована методика выбора мощности, рассмотренная выше.
Достаточно обоснованно также может быть произведена проверка предварительно выбранной мощности двигателя в случае непрерывного слежения с остановками после завершения отработки рассогласования и троганием после достижения моментом двигателя в результате накопления ошибки, величины момента трогания [30]. Такой режим имеет место в фотоэлектрических системах слежения за световыми объектами.
Если речь идет не о следящих системах как таковых, а о позиционном приводе, предназначенном для отработки заданного перемещения из одной точки в другую, т. е. если он работает по трапецеидальной (или треугольной) диаграмме скорости (рис. 2.8), то проверка двигателя по нагреву может быть выполнена классическими методами - методом эквивалентного тока и методом эквивалентного момента [16, 30]. На этапах разгона и торможения следует принять момент, определяемый перегрузочной способностью двигателя.
Если для позиционной системы нагрузочная диаграмма в большинстве случаев может быть определена, то для следящих систем, напротив, она обычно не предсказуема и имеет случайный, но стационарный характер. При этом случайный характер может иметь как поступающий входной сигнал, так и нагрузка на оси двигателя. Например, в системе управления радиолокационной антенной случайный характер обычно имеет радиосигнал,

Рис. 2.8. Трапецеидальный график скорости отработки заданного перемещения и соответствующая диаграмма тока
несущий информацию о координатах летящей цели, а также момент на осях антенны, зависящий от ветрового воздействия на поверхности ее элементов. Соответственно детерминированные методы определения необходимого момента не могут быть использованы и приходится применять приближенные пути расчета, базирующиеся на методах математической статистики. Ориентировочный выбор двигателя должен производиться на основе данных, относящихся к уже действующим установкам. Оценка правильности принятой мощности двигателя может быть произведена по имеющимся данным о величине математического ожидания тока т(1) или момента т(М) согласно формулам:
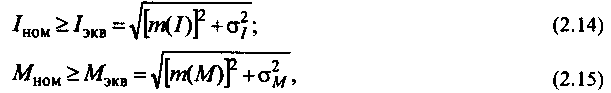
в которых σI и σм -дисперсия (т. е. среднеквадратическое отклонение соответствующей величины от эквивалентного значения). Поведение системы управления при воздействии случайных сигналов и помех весьма подробно изучается в курсе ТАУ, при этом используются характеристики случайных процессов - корреляционная функция R(τ), (где τ - смещение по времени зависимости, вводимой при оценке корреляции) или спектральная плотность S(ω). Как известно, спектральная плотность характеризует распределение мощности сигнала по спектру частот, т. е. представляет квадрат амплитуды гармоники разложения случайной функции в ряд Фурье. Характеристики случайных процессов как корреляционную функцию, так и спектральную плотность обычно определяют по данным экспериментальных исследований установок, аналогичных проектируемой. Еще недавно тратили много времени на ручную обработку осциллограмм. В настоящее время существуют специальные приборы - корреляторы и спектральные анализаторы.
Спектральная плотность легко может быть найдена по корреляционной функции, применив прямое преобразование Фурье,

Для нахождения корреляционной функции может быть использован интеграл Фурье:

На основе выражения

можно найти среднее значение квадрата ошибки системы, обусловленное как сигналом на входе, так и помехой

В этих формулах: G(jω) - частотная передаточная функция системы по ошибке; Фв (jω) - передаточная функция по возмущающему моменту; Sс(ω) - спектральная плотность сигнала; Sм(ω) - спектральная плотность для статического момента, имеющего случайный характер.
Коэффициенты с1 и с2 учитывают некоторые параметры, не вошедшие в передаточную функцию системы, как-то: величина передаточного отношения редуктора, КПД редуктора и др.
Достатдчно глубоко разработанная теория случайных процессов в основном дает возможность оценить погрешность системы и пока не позволяет даже грубо определить необходимую для системы мощность двигателя, хотя дисперсия представляет средний квадрат тока, а следовательно, потери, в том числе потери в обмотке якоря. Также можно отметить, что при линейных характеристиках момент двигателя пропорционален падению скорости при его нагружении.
В связи с изложенным расчет мощности двигателя приходится вести, пользуясь данными, полученными ранее на аналогичных установках.
