4. Расчет контура регулирования скорости.

Объектом управления для этого контура (см. рис.1) является электромеханическое звено собственного объекта и замкнутый контур регулирования тока якоря с оптимизированной передаточной функцией, равной

.

Пренебрегая в знаменателе членами с “” в степени выше первой (малыми второго порядка), получим:

.

В итоге передаточная функция объекта управления в контуре регулирования скорости принимает вид

,

где - большая постоянная времени, а- малая. Далее, по аналогии с синтезом регулятора тока, по передаточной функции объекта управления () с заданными компенсируемой () и не компенсируемой () частями для оптимизации контура регулирования скорости по техническому (модульному) оптимуму необходимо выбрать П – регулятор с коэффициентом передач:

, (1.6)

где - коэффициент передачи обратной связи по скорости. Полученный пропорциональный регулятор реализуется на базе оперативного усилителя с активным сопротивлением обратной связи. Упрощенная схема регулятора скорости приведена на рис.3.2.

А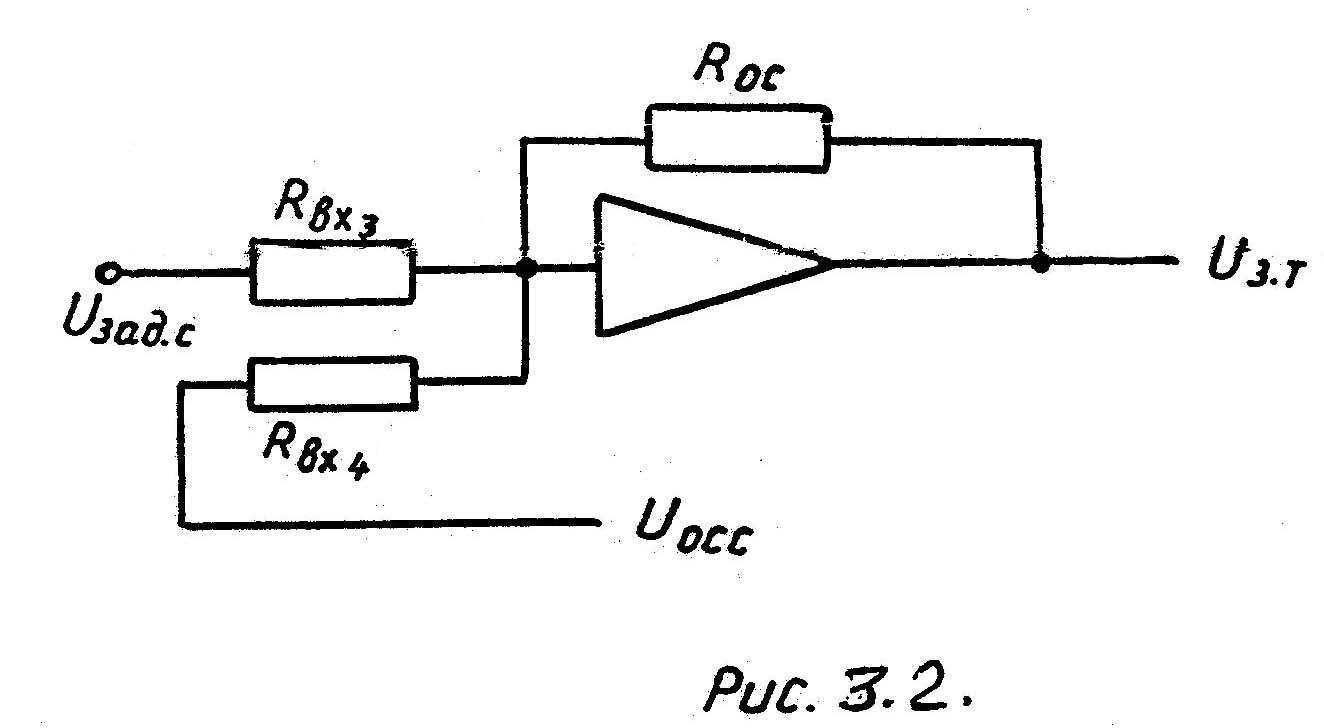налогично ранее рассмотренному при расчете параметров регулятора тока найдем расчетное выражение дляпосле приведения сигнала обратной связи по скорости к задающему входу регулятора с входным сопротивлением:

(1.7)

где В^. с/рад – заданный коэффициент передачи используемого в системе датчика скорости.

Передаточная функция П- регулятора на базе усилителя с активным сопротивлением обратной связи относительно сигнала на имеет вид

. (1.8)

Приравнивая выражения для регулятора скорости по (1.6) и (1.8), получим с учетом выражений (1.2) и (1.7) для иследующие соотношение, связывающее искомые настройки П- регулятора скоростии:

. (1.9)

Здесь входные регуляторы сопротивления тока иуже определены ранее при выборе параметров его настроек.

Подобно выражению (1.5), равенство (1.9) дополняется уравнением связи максимальной величины задающего на входе регулятора скорости с приведенным значениеммаксимального сигнала обратной связи по скорости

, (1.10)

где максимальное значение скорости определено в задании (рад/с), апринимается равным максимальному напряжению при входе стандартного задающего устройства блочной системы регулирования (В).

Два уравнения (1.9) и (1.10) оставляют свободу выбора одной из трех неизвестных ,и. Обычно задаются входным сопротивлением, после чегоипоследовательно определяется из соотношений (1.9) и (1.10). Задавая,кОм, вычислим последовательно искомые параметры,,:

кОм;

кОм;

.

Следующий этап – статистический расчет синтезированной системы как по отношению к задающему, так и по возмущающим воздействиям, а также анализ переходного процесса при ударном приложении нагрузки. Необходимо ответить, что синтезированная выше САУ обеспечивает астатизм системы по отношению к задающему воздействию. Однако при пропорциональном регуляторе скорости этот астатизм создаётся за счет интегрирующего электромеханического звена в структуре объекта и не сохраняется по отношению к основному возмущающему воздействию – нагрузке на валу двигателя. Поэтому, если к системе предъявляются определенные требования к точности стабилизации скорости при вариациях нагрузки в установившихся режимах её работы, необходимо выяснить, удовлетворяются ли они выбранным П – регулятором скоростного контура. Статистические свойства контура регулирования скорости существенно улучшается при его настройке на симметричный оптимум, для которого регулятор всегда содержит интегрирующее звено. В этом случае в системе регулирования скорости обеспечивается астатизм как по отношению к задающему, так и возмущающим воздействиям, что приводит, в частности, к полной компенсации помехи нагрузки. Если при этом соответствующие показатели переходного процесса могут считаться удовлетворительными, то настройка скоростного контура на симметричный оптимум предпочтительна.