
- •Методичні вказівки
- •6.050101 «Комп`ютерні науки»
- •Завдання для розрахунково-графічної роботи
- •Приклад розв’язання задачі
- •Постановка задачі
- •Розв’язання задачі
- •Алгоритм задачі
- •Реалізація програми
- •Демонстрація роботи програми
- •Завдання для самостійного опрацювання
- •Логіка висловлювань
- •Теорія множин
- •Комбінаторний аналіз
- •Теорія графів
- •Література
Завдання для самостійного опрацювання
-
Логіка висловлювань
-
Побудувати таблиці істинності для кожного з висловлювань: а)
 ; б)
; б)
 ; в)
; в)
 ; г)
; г)
 .
. -
Довести, що формули
 ,
,
 ,
,
 ,
,
 ,
де
,
де
 - значення «хибності», мають ту саму
таблицю істинності, що й формула
- значення «хибності», мають ту саму
таблицю істинності, що й формула
 .
. -
Довести, що формули
 та
та
 мають однакові таблиці істинності.
мають однакові таблиці істинності. -
Застосувавши таблиці істинності, довести закони дистрибутивності.
-
Застосувавши таблиці істинності, довести закони де Моргана.
-
Побудувати складне висловлювання, яке складається з простих висловлювань
 ,
,
 ,
,
 та набуває значення
та набуває значення
 тоді й лише тоді, коли:
а)
тоді й лише тоді, коли:
а)
 та
та
 істині,
істині,
 хибне; б) точно два з трьох висловлювань
хибне; б) точно два з трьох висловлювань
 ,
,
 ,
,
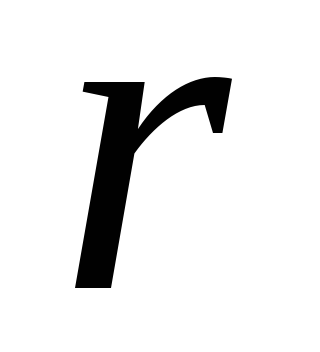 істинні.
істинні.
-
Теорія множин
-
Задано множини
 ,
,
 ,
,
 .
Побудувати Декартові добутки:
а)
.
Побудувати Декартові добутки:
а)
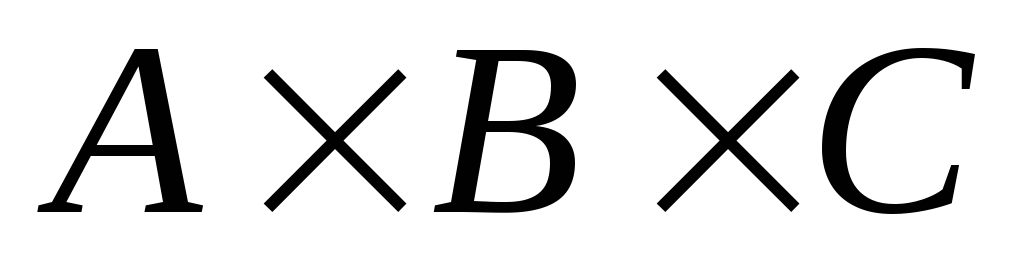 ; б)
; б) ; в)
; в)
 ; г)
; г)
 .
. -
Задано множини
 та
та
 .
Побудувати множини:
а)
.
Побудувати множини:
а)
 ; б)
; б)
 ; в)
; в)
 ; г)
; г)
 .
. -
Знайти множини
 та
та
 ,
якщо
,
якщо
 ,
,
 ,
і
,
і

 .
. -
Довести рівність
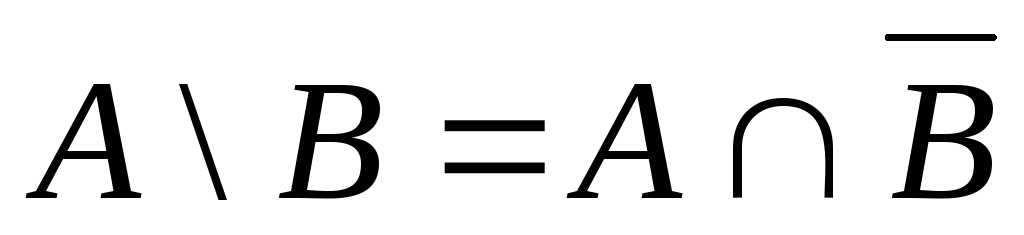 .
. -
Задано універсальну множину

 :
а)
подати бітовими рядками множини
:
а)
подати бітовими рядками множини
 ,
,
 ,
,
 ;
б)
відновити множини за бітовими рядками
0101111100, 1000000001, 1111111111.
;
б)
відновити множини за бітовими рядками
0101111100, 1000000001, 1111111111. -
Показати, як можна використати операції над бітовими рядками для знаходження значень виразів: а)
 ; б)
; б)
 ;
в)
;
в)
 ; г)
; г)
 .
Тут
універсальна множина
.
Тут
універсальна множина
 - латинський алфавіт, якай складається
з 26 букв, а множини
- латинський алфавіт, якай складається
з 26 букв, а множини
 ,
,
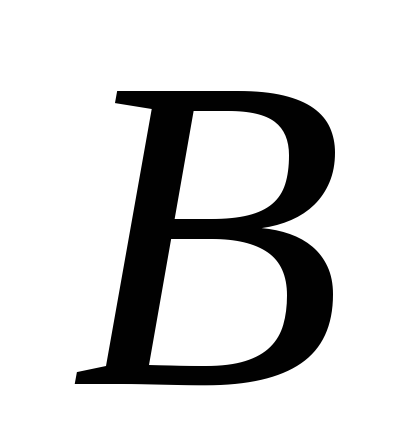 ,
,
 та
та
 такі:
такі:
 ,
,

 ,
,
 ,
,
 .
.
-
Комбінаторний аналіз
-
Нехай
 .
Навести всі розміщення та сполучення
без повторень з елементів множини
.
Навести всі розміщення та сполучення
без повторень з елементів множини
 по 3 елементи.
по 3 елементи. -
Обчислити кількість перестановок множини
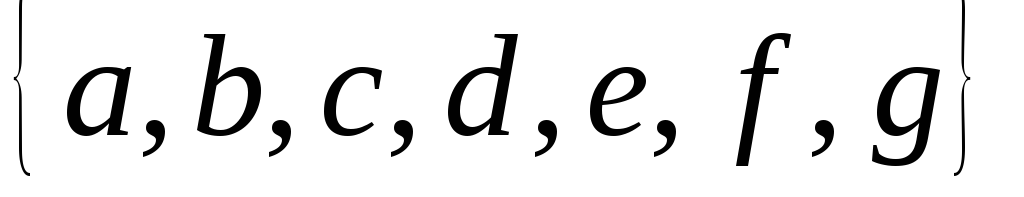 ,
які закінчуються буквою
,
які закінчуються буквою
 .
. -
Обчислити значення: а)
 ; б)
; б)
 ; в)
; в)
 ; г)
; г)
 ; д)
; д)
 ; е)
; е)
 ;
ж)
;
ж)
 ; з)
; з)
 ; и)
; и)
 ; к)
; к)
 ; л)
; л)
 ; м)
; м)
 .
. -
У групі
 чоловіків і
чоловіків і
 жінок. Скількома способами їх можна
вишикувати в шеренгу так, щоб чергувалися
чоловік і жінка?
жінок. Скількома способами їх можна
вишикувати в шеренгу так, щоб чергувалися
чоловік і жінка? -
Скількома способами можна розсадити шістьох осіб за круглим столом?
-
Із цифр 1, 2, 3, 4, 5, не повторюючи їх, скласти всі можливі п’ятицифрові числа. Скільки серед них таких чисел: а) які починаються цифрою 3; б) не починаються цифрою 5; в) починаються з 54?
-
Знайти кількість розв’язків наведених нижче рівнянь у невід’ємних цілих числах: а)
 ; б)
; б)
 .
. -
Побудувати розклад: а)
 ; б)
; б)
 ; в)
; в)
 ; г)
; г)
 .
. -
Скільки членів у розкладі
 ?
? -
Записати розклад
 .
. -
Знайти коефіцієнти при
 у розкладі
у розкладі
 .
. -
Описати алгоритм побудови розміщень по
 елементів множини з
елементів множини з
 елементів. За його допомогою виписати
всі розміщення по два елементи множини
{1,2,3,4,5}.
елементів. За його допомогою виписати
всі розміщення по два елементи множини
{1,2,3,4,5}.
-
Теорія графів
-
Знайти кількість вершин, ребер і степені кожної вершини неорієнтованих графів: а)
 б)
б)

-
Знайти суму степенів вершин кожного з графів задачі 1 та переконатись, що вона вдвічі більша за кількість ребер графа.
-
Визначити кількість вершин та дуг і знайти напівстепені входу й виходу для кожної вершини орієнтованих мультиграфів: а)
 б)
б)

-
Для кожного з графів задачі 3 знайти суму напівстепенів входу та суму напівстепенів виходу вершин. Переконатись, що кожна з них дорівнює кількості дуг графа.
-
Скільки вершин і ребер мають наведені нижче графи: а)
 ; б)
; б)
 ; в)
; в)
 ; г)
; г)
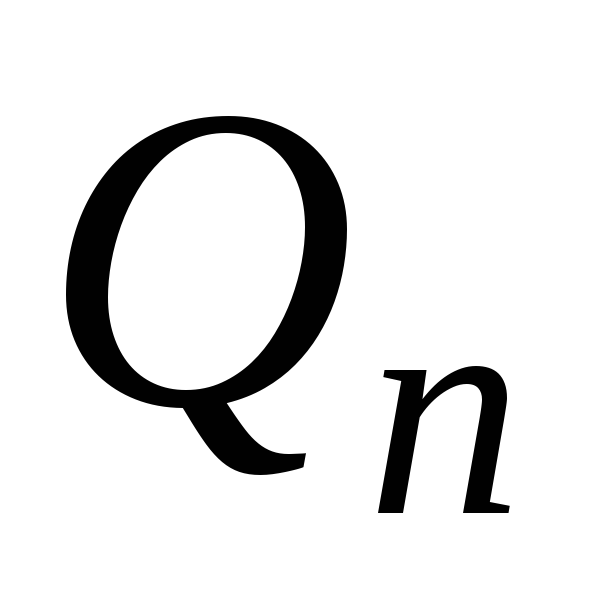 ; д)
; д)
 .
. -
Скільки ребер має граф, у якого вершини мають такі степені: 4, 3, 3, 2, 2?
-
Зобразити орієнтовані графи за матрицями суміжності: а)
 ; б)
; б)
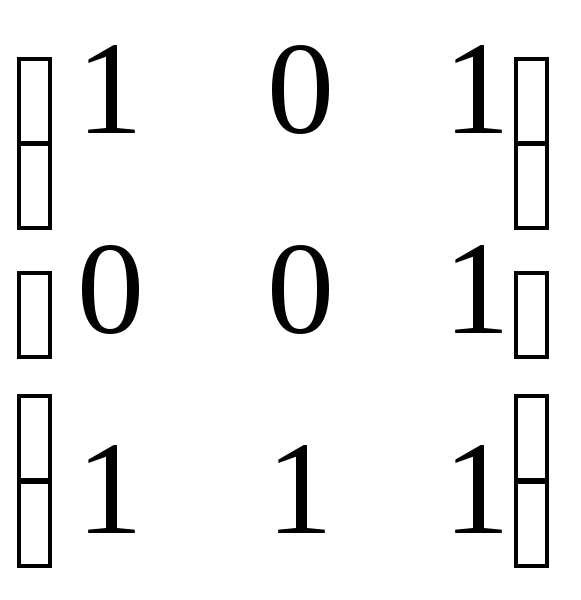 ; в)
; в)
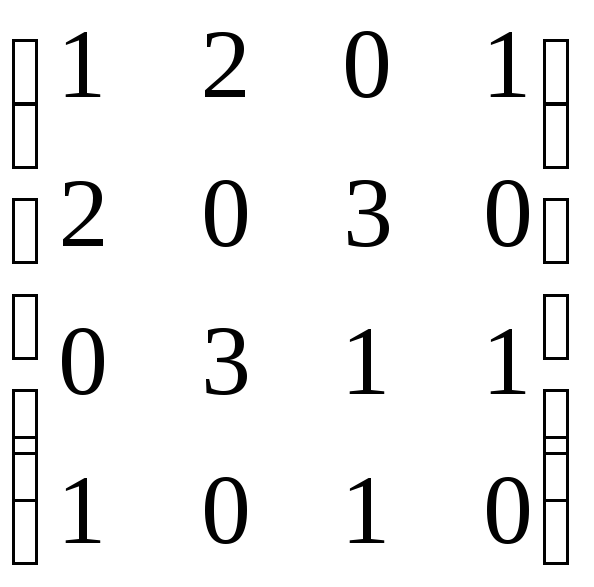 .
. -
Зобразити орієнтовані графи за матрицями суміжності: а)
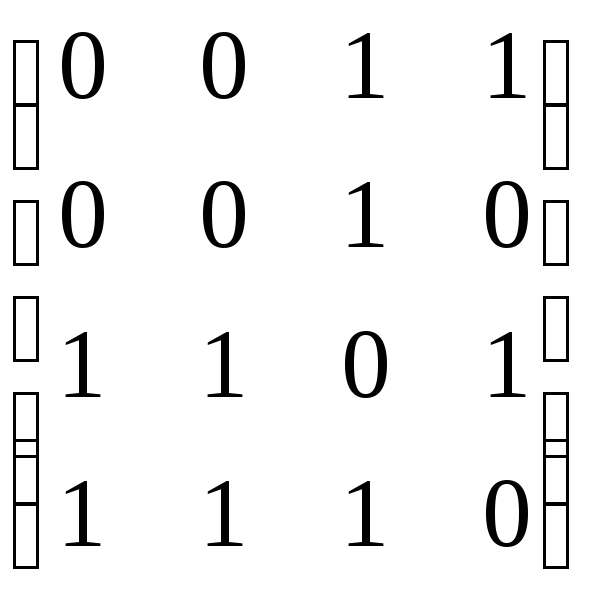 ; б)
; б)
 .
. -
