Алгоритм симплекс-метода:

1. Определить число и состав базисных и свободных переменных.

2. Выразить базисные переменные через свободные переменные.

3. Выразить целевую функцию через свободные переменные.

4. Построить начальную симплекс-таблицу.

5. Проверить решение на оптимальность: если в F-строке (кроме С₀) все С_j0, то получено оптимальное решение: X=(B₁,...,B_m,0,...,0), F=C₀. Если же существует C_j<0, то решение можно улучшить, но предварительно надо проверить факт существования решения.

6. Проверить существование решения: рассмотрим все столбцы, у которых С_j<0, если существует хотя бы один столбец, у которого все коэффициенты A_i,j<0, то задача решения не имеет, т.к. множество допустимых решений D не ограничено и целевая функция неограниченно возрастает. Если таких столбцов нет, то переходим к следующему этапу.

7. Выбрать свободную переменную, которую надо ввести в базис (выбор разрешающего столбца): это столбец, с минимальным значением С_j (пусть это k-й столбец)

8. Выбрать базисную переменную, которую надо вывести из базиса (выбор разрешающей строки): рассмотрим k-й столбец и все его элементы, которые больше нуля, т.е. A_i,k>0; для всех этих элементов находим отношение B_i/A_i,k и выбираем строку, которая соответствует минимальному значению этого отношения (пусть это i-я строка); соответствующая i-я переменная X_i выводится из базиса; при нескольких одинаковых отношениях берем любую строку; элемент A_i,k называется разрешающим элементом.

9. Пересчитать симплекс-таблицу: составляем новую симплекс-таблицу заменив в составе базисных переменных X_i на X_k; заполняем сначала новую k-ю строку, записывая в нее элементы старой i-ой строки, поделенные на разрешающий элемент; после заполнения k-ой строки заполняем оставшиеся строки; для этого k-ю строку умножаем последовательно на такие числа, чтобы после сложения ее с каждой строкой старой таблицы в k-ом столбце получить везде ноль (кроме единицы в k-ой строке).

10. Когда в F-строке все коэффициенты (кроме С₀) будут больше нуля, тогда получаем оптимальное решение,

11. Когда существует столбец , у которого C_j<<0 и все коэффициенты A_i,j<<0, в этом случае решения на существует.

12. После заполнения новой симплекс-таблицы, если все еще есть решение но не найдено оптимальное алгоритм возвращается к 5-му пункту.

Алгоритм двойственного симплекс-метода.

Согласно книге Томаса Кормена "Алгоритмы: построение и анализ" двойственный симплекс-метод, как и симплекс-метод, используется при нахождении решения задачи линейного программирования, записанной в форме основной задачи, для которой среди векторов , составленных из коэффициентов при неизвестных в системе уравнений, имеется m единичных. Вместе с тем двойственный симплекс–метод можно применять при решении задачи линейного программирования, свободные члены системы уравнений которой могут быть любыми числами (при решении задачи симплексным методом эти числа предполагались неотрицательными). Такую задачу и рассмотрим теперь, предварительно предположив, что единичными являются векторы  т. е. рассмотрим задачу, состоящую в определении максимального значения функции (3.1)

при условиях

(3.2)

(3.3)

где

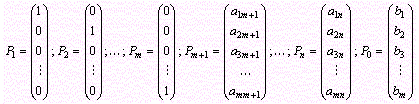
и среди чисел имеются отрицательные.

В данном случае есть решение системы линейных уравнений (3.2). Однако это решение не является планом задачи (3.1) – (3.3), так как среди его компонент имеются отрицательные числа.

Поскольку векторы – единичные, каждый из векторов можно представить в виде линейной комбинации данных векторов, причем коэффициентами разложения векторов по векторам служат числа Таким образом, можно найти

Определение:

Решение системы линейных уравнений (3.2), определяемое базисом , называется псевдопланом задачи (3.1) – (3.3), еслидля любого 

Теорема:

Если в псевдоплане , определяемом базисом , есть хотя бы одно отрицательное число такое, что все ,то задача (3.1) – (3.3) вообще не имеет планов.

Теорема:

Если в псевдоплане , определяемом базисом , имеются отрицательные числа такие, что для любого из них существуют числа a_ij<0, то можно перейти к новому псевдоплану, при котором значение целевой функции задачи (3.1) – (3.3) не уменьшится.

Сформулированные теоремы дают основание для построения алгоритма двойственного симплекс-метода.

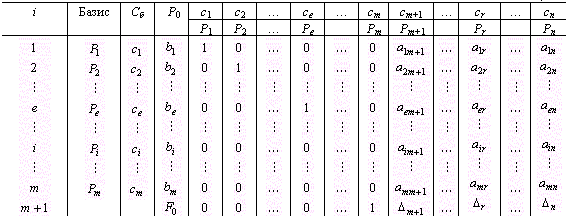
Итак, продолжим рассмотрение задачи (3.1) – (3.3). Пусть – псевдоплан этой задачи. На основе исходных данных составляют симплекс-таблицу (табл. 1), в которой некоторые элементы столбца вектора являются отрицательными числами. Если таких чисел нет, то в симплекс-таблице записан оптимальный план задачи (3.1) – (3.3), поскольку, по предположению, все . Поэтому для определения оптимального плана задачи при условии, что он существует, следует произвести упорядоченный переход от одной симплекс–таблицы к другой до тех пор, пока из столбца вектора не будут исключены отрицательные элементы. При этом все время должны оставаться неотрицательными все элементы (т +1)–й строки, т.е. для любого 

Таким образом, после составления симплекс-таблицы проверяют, имеются ли в столбце вектора отрицательные числа. Если их нет, то найден оптимальный план исходной задачи. Если же они имеются (что мы и предполагаем), то выбирают наибольшее по абсолютной величине отрицательное число. В том случае, когда таких чисел несколько, берут какое–нибудь одно из них: пусть это число b_l. Выбор этого числа определяет вектор, исключаемый из базиса, т. е. в данном случае из базиса выводится вектор P_l. Чтобы определить, какой вектор следует ввести в базис, находим , где 

Пусть это минимальное значение принимается при , тогда в базис вводят вектор Р_r. Число является разрешающим элементов. Переход к новой симплекс–таблице производят по обычным правилам симплексного метода. Итерационный процесс продолжают до тех пор, пока в столбце вектора Р₀ не будет больше отрицательных чисел. При этом находят оптимальный план исходной задачи, а следовательно, и двойственной. Если на некотором шаге окажется, что в i–й строке симплекс–таблицы (табл. 1) в столбце вектора Р₀ стоит отрицательное число b_i, а среди остальных элементов этой строки нет отрицательных, то исходная задача не имеет решения.

Таким образом, отыскание решения задачи (3.1) – (3.3) двойственным симплекс-методом включает следующие этапы:

1. Находят псевдоплан задачи.

2. Проверяют этот псевдоплан на оптимальность. Если псевдоплан оптимален, то найдено решение задачи. В противном случае либо устанавливают неразрешимость задачи, либо переходят к новому псевдоплану.

3. Выбирают разрешающую строку с помощью определения наибольшего по абсолютной величине отрицательного числа столбца вектора Р₀ и разрешающий столбец с помощью нахождения наименьшего по абсолютной величине отношения элементов (m+1)–и строки к соответствующим отрицательным элементам разрешающей строки.

4. Находят новый псевдоплан и повторяют все действия начиная с этапа 2.

Таблица 1