- •1. Теоретические основы. Двойственный симплекс метод.
- •Алгоритм симплекс-метода:
- •2. Практическая задача
- •2.1 Постановка задачи
- •2.2 Решение задачи
- •3. Разработка программного обеспечения
- •3.1 Входные данные
- •3.2 Выходные данные
- •3.3 Основные функции программного обеспечения
- •3.4 Блок-схема
- •3.5 Интерфейс программы
- •3.6 Руководство по эксплуатации
- •4. Проведение исследования
- •Заключение
- •Список используемой литературы
- •Приложение
2. Практическая задача
2.1 Постановка задачи
Для изготовления четырех видов продукции предприятие использует три типа ресурсов. Нормы расхода ресурсов каждого типа на единицу продукции, их наличие в распоряжении предприятия, а также цена единицы продукции приведены в таблице 2.
Таблица 2
|
Тип ресурса |
Норма расхода ресурсов на единицу продукции |
Наличие ресурса |
||||
|
A |
B |
C |
D |
|
||
|
I |
1 |
0 |
2 |
1 |
180 |
|
|
II |
0 |
1 |
3 |
2 |
210 |
|
|
III |
4 |
2 |
0 |
4 |
800 |
|
|
Цена единицы продукции |
9 |
6 |
4 |
7 |
|
|
Требуется:
а) Сформулировать двойственную задачу и найти оптимальные планы прямой и двойственной задач;
б) Найти интервалы устойчивости двойственных оценок по отношению к изменениям ресурсов каждого типа;
в) Выявить изменение общей стоимости изготовляемой продукции, определяемой оптимальным планом ее производства при уменьшении количества ресурса I типа на 60 ед. и увеличении количества ресурсов II и III типов соответственно на 120 и 160 ед. Провести анализ возможного изменения общей стоимости продукции как при изменении объемов каждого из ресурсов по отдельности, так и при их одновременном изменении в указанных размерах.
Математическая постановка прямой задачи:
L = 9x1 + 6x2 + 4x3 + 7x4 → max
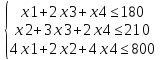
Математическая постановка двойственной задачи:
W =180z1 + 210z2 + 800z3 → min

2.2 Решение задачи
а) Решение прямой задачи:
Математически сформулируем прямую задачу:
L = 9x1 + 6x2 + 4x3 + 7x4 → max
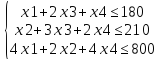
Убираем неравенства:
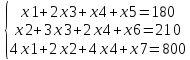
Составляем таблицу:
|
I |
Б |
Сб |
Р0 |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 |
Р7 |
Отн |
|
1 |
Р5 |
0 |
180 |
1 |
0 |
2 |
1 |
1 |
0 |
0 |
180 |
|
2 |
Р6 |
0 |
210 |
0 |
1 |
3 |
2 |
0 |
1 |
0 |
|
|
3 |
Р7 |
0 |
800 |
4 |
2 |
0 |
4 |
0 |
0 |
1 |
200 |
|
∆ |
|
|
|
-9 |
-6 |
-4 |
-7 |
0 |
0 |
0 |
|
К=1; R=1;
x1=0; x2=0; x3=0; x4=0; x5=180; x6=210; x7=800; L=0;
В таблице присутствуют отрицательные ∆, поэтому пересчитаем таблицу, добавив в базис Р1 и убрав Р5:
|
I |
Б |
Сб |
Р0 |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 |
Р7 |
Отн |
|
1 |
Р1 |
9 |
180 |
1 |
0 |
2 |
1 |
1 |
0 |
0 |
|
|
2 |
Р6 |
0 |
210 |
0 |
1 |
3 |
2 |
0 |
1 |
0 |
210 |
|
3 |
Р7 |
0 |
80 |
0 |
2 |
-8 |
0 |
-4 |
0 |
1 |
40 |
|
∆ |
|
|
|
0 |
-6 |
14 |
2 |
9 |
0 |
0 |
|
К=2; R=3;
x1=180; x2=0; x3=0; x4=0; x5=0; x6=210; x7=80; L=1620;
В таблице присутствуют отрицательные ∆, поэтому пересчитаем таблицу, добавив в базис Р2 и убрав Р7:
|
I |
Б |
Сб |
Р0 |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 |
Р7 |
Отн |
|
1 |
Р1 |
9 |
180 |
1 |
0 |
2 |
1 |
1 |
0 |
0 |
180 |
|
2 |
Р6 |
0 |
170 |
0 |
0 |
7 |
2 |
2 |
1 |
-0.5 |
85 |
|
3 |
Р2 |
6 |
40 |
0 |
1 |
-4 |
0 |
-2 |
0 |
0.5 |
-20 |
|
∆ |
|
|
|
0 |
0 |
-10 |
2 |
-3 |
0 |
3 |
|
К=5; R=2;
x1=180; x2=40; x3=0; x4=0; x5=0; x6=170; x7=0; L=1860;
В таблице присутствуют отрицательные ∆, поэтому пересчитаем таблицу, добавив в базис Р5 и убрав Р6:
|
I |
Б |
Сб |
Р0 |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 |
Р7 |
Отн |
|
1 |
Р1 |
9 |
95 |
1 |
0 |
-1.5 |
0 |
0 |
-0.5 |
0.25 |
|
|
2 |
Р5 |
0 |
85 |
0 |
0 |
3.5 |
1 |
1 |
0.5 |
-0.25 |
|
|
3 |
Р2 |
6 |
210 |
0 |
1 |
3 |
2 |
0 |
1 |
0 |
|
|
∆ |
|
|
|
0 |
0 |
0.5 |
5 |
0 |
1.5 |
2.25 |
|
x1=95; x2=210; x3=0; x4=0; x5=85; x6=0; x7=0; L=2115;
В таблице отсутствуют отрицательные ∆, следовательно данное решение оптимально.
Решение двойственной задачи:
Математически сформулируем двойственную задачу:
W =180y1 + 210y2 + 800y3 → min
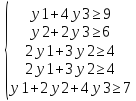
Используя решение прямой задачи видим, что оптимальным будет решение
y1=0; y2=1.5; y3=2.25;
б) Найдем промежутки устойчивости двойственных оценок по отношению к изменениям ресурсов каждого типа. Для этого, используя данные таблицы из предыдущего действия, перемножим матрицы:
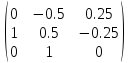 *
*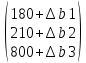 =
=

определим, при каких значениях Δb1 , Δb2 , Δb3 элементы матрицы неотрицательны
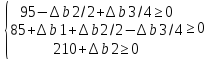
из этой системы можно сделать вывод, что:
1) при
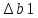 =0
и
=0
и
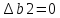 -380≤∆b3≤340 следовательно
если количество ресурсов 3го типа
-380≤∆b3≤340 следовательно
если количество ресурсов 3го типа
 меняется
в промежутке (420;1140) а количество других
ресурсов не меняется, то двойственная
задача сохраняет свой оптимальный план.
меняется
в промежутке (420;1140) а количество других
ресурсов не меняется, то двойственная
задача сохраняет свой оптимальный план.
2) при
 =0
и
=0
и
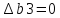 -170≤∆b2≤190 следовательно
если количество ресурсов 2го типа
-170≤∆b2≤190 следовательно
если количество ресурсов 2го типа
 меняется
в промежутке (40;400) а количество других
ресурсов не меняется, то двойственная
задача сохраняет свой оптимальный план.
меняется
в промежутке (40;400) а количество других
ресурсов не меняется, то двойственная
задача сохраняет свой оптимальный план.
3) при
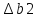 =0
и
=0
и
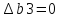 -85≤∆b1 следовательно
если количество ресурсов 1го типа
-85≤∆b1 следовательно
если количество ресурсов 1го типа
 меняется
в пределе 85 а количество других ресурсов
не меняется, то двойственная задача
сохраняет свой оптимальный план.
меняется
в пределе 85 а количество других ресурсов
не меняется, то двойственная задача
сохраняет свой оптимальный план.
в) Количество единиц первого ресурса уменьшается на 60, следовательно ∆b1=-60.
Количество единиц 2го и 3его ресурсов увеличивается на 120 и 160 соответственно, следовательно ∆b2=120 и ∆b3=160. Чтобы выяснить останется ли прежний план оптимальным при одновременном изменении, подставим эти значения в систему.
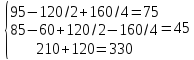
из того, что все выражения принимают положительное значение, следует, что оптимальный план останется прежним.
Это позволяет определить приращение максимального значения
функции L при указанных изменениях количества ресурсов.
∆Lmax = y1∙∆b1 + y2∙∆b2 + y3∙∆b3 = 0∙(-60)+1.5∙120+2.25∙160=540
Из этого следует, что если изменить количество ресурсов таким образом, оптимальный план будет приносить на 540 больше прибыли.
Далее, рассматривая эту формулу, можно заметить, что уменьшение количества 1го ресурса ни на что не влияет, а увеличение количества 2го и 3его увеличивает максимальное значение функции.