3. Свойства определителей.

Выберем в -матрице произвольные строк с номерами и столбцов с номерами (). Стоящие на пересечении этих строк и столбцов элементы образуют -матрицу. Определитель этой матрицы называется минором -го порядка; обозначим его через . Вычеркнем теперь выбранные строки и столбцы. Останется -матрица. Ee определитель – минор порядка ; обозначим его через ( черта над буквой означает, что строки с номерами и столбцы с номерами были вычеркнуты). называется минором, дополнительным к минору . Число называется алгебраическим дополнением минора .

Пример. Выберем одну -ую строку и один -ый столбец. На их пересечении стоит элемент матрицы . Минор 1-го порядка . – минор -го порядка, а – алгебраическое дополнение элемента .

Теорема 1. Для любого номера строки справедливо равенство .

Доказательство. Выразим через элементы матрицы :

, (1)

где суммирование ведется по всем перестановкам () чисел ( среди них нет числа ). Умножим равенство (1) на :

. (2) Рассмотрим перестановку () всех первых натуральных чисел; сравним ее четность с четностью перестановки () , в которой нет числа . Для этого введем перестановку чисел (). Среди имеется ровно чисел, меньших числа . Поэтому . А перестановка получается из перестановки () при помощи транспозиции; при этом четность перестановки меняется раз. Следовательно,

,

или, что то же самое,

.

Поэтому (2) можно записать в виде

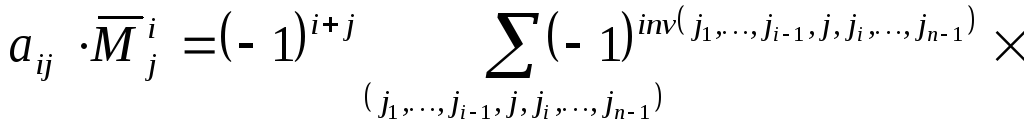
, (3)

где суммирование ведется по всем перестановкам чисел , у которых на -ом месте стоит фиксированное число . Умножим равенство (3) на , а затем сложим полученного вида равенства по всем . Тогда будут пробегать уже все без исключения перестановки чисел , и в правой части равенства мы получим .

Теорема 1 утверждает, что определитель матрицы равен сумме вдоль -ой строки произведений элементов этой строки на их алгебраические дополнения. Поэтому она называется теоремой о разложении определителя по строке. Вычисление сведено к вычислению определителей порядка .

Теорема 2. .

Доказательство. является суммой произведений , взятых со знаком, который определяется четностью перестановки (). Если транспонировать матрицу , то все множители такого произведения останутся в разных строках и разных столбцах матрицы . Значит, это произведение войдет с некоторым знаком в . Очевидно,

.

Упорядочим множители в правой части последнего равенства в порядке возрастания номеров строк матрицы . Тогда перестановка индексов столбцов будет иметь ту же четность, что и перестановка (). Поэтому знак рассматриваемого члена в будет таким же, каким был его знак в . Оба определителя состоят из одних и тех же членов с одинаковыми знаками. 

Теорема 3. Для любого номера столбца справедливо равенство .

Доказательство. . По теореме 2 алгебраическое дополнение элемента в матрице и алгебраическое дополнение элемента в матрице совпадают. Обозначим через минор, дополнительный к в матрице . Тогда по теореме 1

.

Но по теореме 2 .

Теорема 3 утверждает, что определитель матрицы равен сумме вдоль -го столбца произведений элементов этого столбца на их алгебраические дополнения. Она называется теоремой о разложении определителя по столбцу.

Теоремы 1,2,3 говорят о равноправии строк и столбцов в определении .

Задача. Сформулируйте определение , эквивалентное данному выше, переставив роли строк и столбцов.

Теоремы 1,3 являются частными случаями более общей теоремы:

Теорема 4. (Теорема Лапласа). Пусть в -матрице А произвольно выбраны строк (). Тогда равен сумме произведений всех миноров -го порядка, содержащихся в этих строках, на их алгебраические дополнения.

( Без доказательства. Доказательство можно провести индукцией по ; см. , например, [1]).

Теорема Лапласа утверждает, что для любых выбранных номеров строк выполнено равенство

,

где суммирование ведется по всем наборам индексов , удовлетворяющим условиям . Разумеется, строки и столбцы в этой теореме можно поменять ролями:

Теорема 4*. Пусть в -матрице произвольно выбраны столбцов (). Тогда равен сумме произведений всех миноров -го порядка, содержащихся в этих столбцах, на их алгебраические дополнения.

Теперь легко получить свойства определителя.

Свойство 1. При перестановке местами двух строк (или двух столбцов) матрицы ее определитель сохраняет свою абсолютную величину, но меняет знак на противоположный.

Доказательство. В силу равноправия строк и столбцов достаточно доказать данное утверждение лишь для строк. Заметим, что 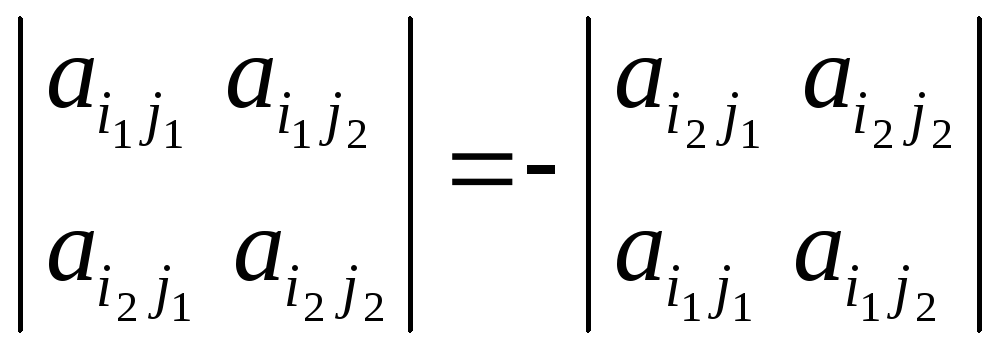. Пусть в матрице меняются местами -ая и -ая строки. По теореме Лапласа

, и, как мы только что видели, при перестановке -ой и -ой строк определители второго порядка меняют знаки. А дополнительные миноры не зависят от перестановки указанных строк, поскольку получены вычеркиванием их. 

Свойство 2. Пусть-матрицы отличаются только -ой строкой, причем

.

Тогда .

(Аналогичное свойство имеет место и в случае, когда отличаются только -ым столбцом, причем этот столбец матрицы является линейной комбинацией соответствующих столбцов матриц и .)

Доказательство. Каждый определитель разложим по -ой строке. У этих определителей дополнительные миноры элементов -ой строки одинаковы. Поэтому требуемое утверждение следует из равенств .

Свойство 3. Если в матрице есть две одинаковые строки (два одинаковых столбца), то .

Доказательство. При перестановке одинаковых строк не изменится, а по свойству 1 он должен поменять знак на противоположный. 

Свойство 4. Если все элементы некоторой строки (некоторого столбца) умножить на одно и то же число , то определитель матрицы умножится на .

Доказательство следует из свойства 2 при или непосредственно из определения .

Свойство 5. Если все элементы некоторой строки (некоторого столбца) равны нулю, то определитель матрицы равен нулю.

Доказательство следует из свойства 4 при или непосредственно из определения .

Свойство 6. Если в матрице есть две пропорциональные строки (два пропорциональных столбца), то ее определитель равен нулю.

Доказательство следует из свойств 3 и 4. 

Свойство 7. Если к строке матрицы прибавить линейную комбинацию некоторых строк этой же матрицы, то определитель не изменится. (То же верно и для столбцов.)

Доказательство. К определителю матрицы мы прибавляем равный нулю определитель. 