2. 2 Оценка точности функций измеренных величин

В геодезии часто искомые величины находят в результате вычислений, как функции измеренных величин (аргументов). Очевидно, что ошибка функции будет зависеть как от ошибок измерения аргументов, так и от вида функции.

1. 2.1 Средняя квадратическая ошибка функции

Пусть дана функция

,

где  величины  — измерены независимо. Известны их средние квадратические ошибки .

Средняя квадратическая ошибка функции (2.1) вычисляется по формуле:

.

Если величины коррелированы, т.е. коэффициенты попарной корреляционной связи отличны от нуля, , то средняя квадратическая ошибка функции вычисляется по формуле:

.

где 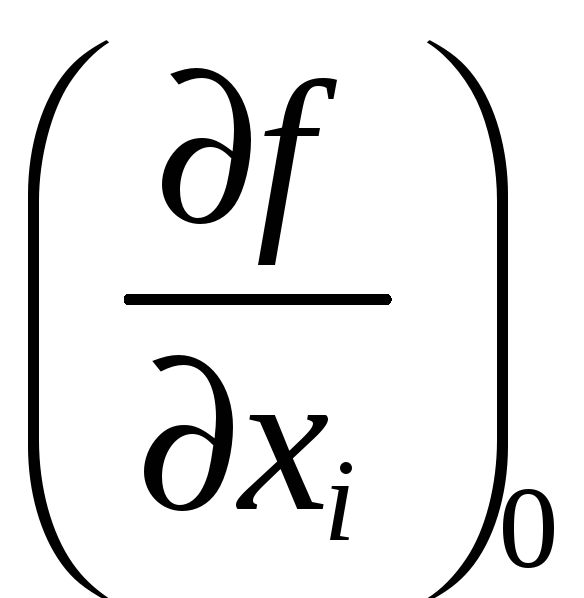 — частные производные функции, взятые по точным значениям величин Х_i, но вычисленные по их приближённым значениям, в качестве которых принимают измеренные значения  х_i, близкие к точным значениям.

Предрасчёт ожидаемой средней квадратической ошибки функции по формулам  и  называют решением прямой задачи теории ошибок.

Задача 2.1. В треугольнике измерены два угла, известны их средние квадратические ошибки , . Найти среднюю квадратическую ошибку третьего угла, вычисленного по двум измеренным.

Решение. Составляем функцию ; имеем:

; ;

 — точное число; x₁ и x₂ — независимо измеренные углы.

Тогда по формуле  имеем:

; .

Задача 2.2. Определить среднюю квадратическую ошибку превышения, вычисленного по формуле , где S — горизонтальное проложение,  — угол наклона. Известно, что ; ; ; ; .

Решение. Находим и по формуле  его среднюю квадратическую ошибку m_h:

^),

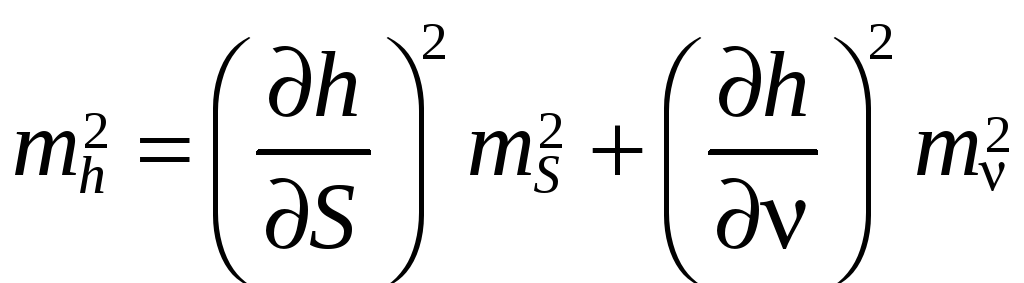где

; .

Тогда

.

; ; ; .

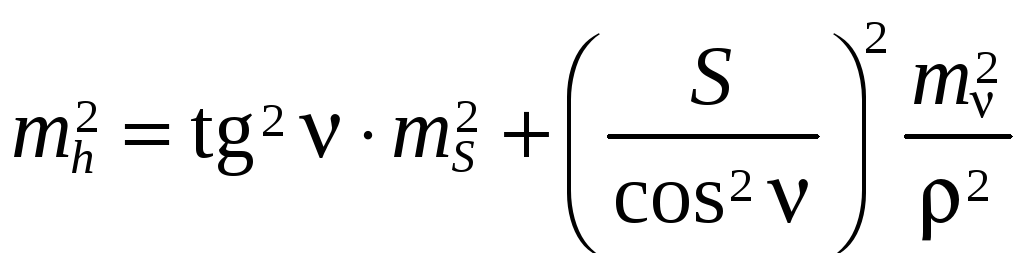Известно, что величина m_h должна быть получена с двумя (или тремя, если число начинается с единицы) значащими цифрами. Чтобы это требование обеспечить, необходимо в промежуточных вычислениях по формуле  удерживать в числах на одну значащую цифру больше, т.е. оставлять три (или четыре) значащие цифры, а сами числа следует представлять в стандартной форме. Например, число 0,04366² необходимо записать так: ; число 3438² следует записать так: . Такие действия позволят упростить вычисления по формуле  и, кроме того, дадут представление о величине влияния каждого источника ошибок на общую среднюю квадратическую ошибку функции.

С учётом сказанного выше находим:

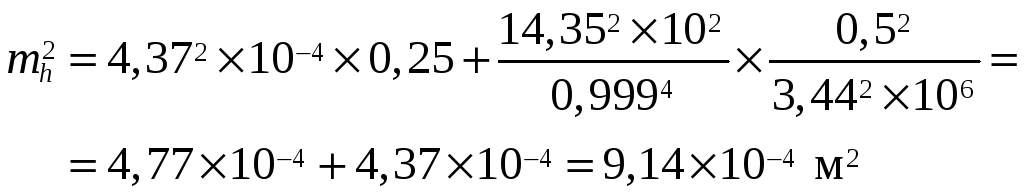
По результатам вычислений видно, что влияние линейных и угловых ошибок измерений в данной задаче примерно одинаково. Окончательно получаем:

.

Ответ: .

При решении обратной задачи теории ошибок — расчёте точности измерений аргументов по заданной средней квадратической ошибке функции — применяют так называемый принцип равных влияний, требование которого состоит в том, чтобы влияние каждого источника ошибок на общую ошибку функции было одинаковым.

Так из формулы  следует:

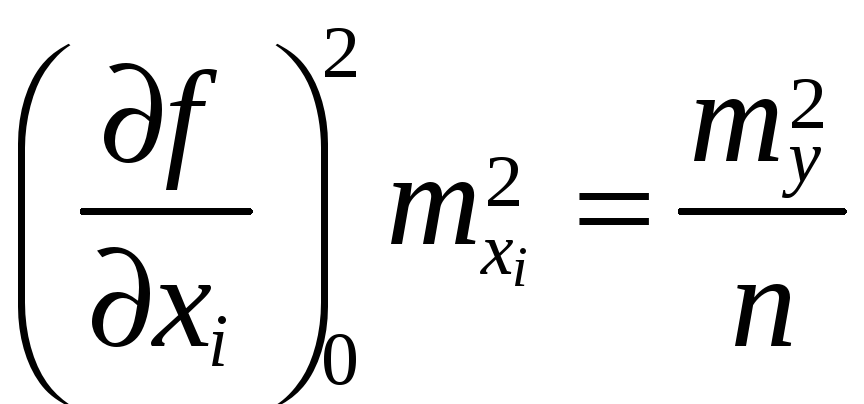и

.

Все  находят из решения уравнений .

Задачи для контроля. Найти средние квадратические ошибки следующих функций независимо измеренных величин:

1) ;

2) ;

3) ;

4) ;

5) .
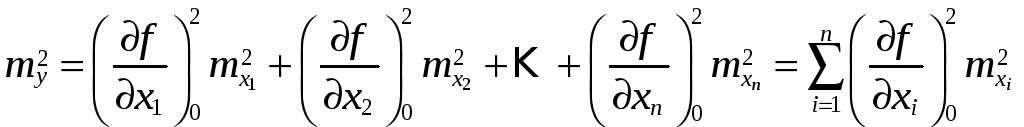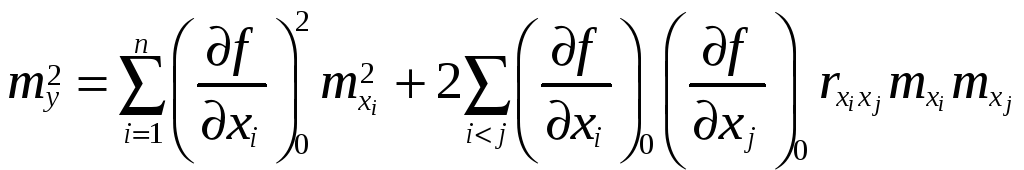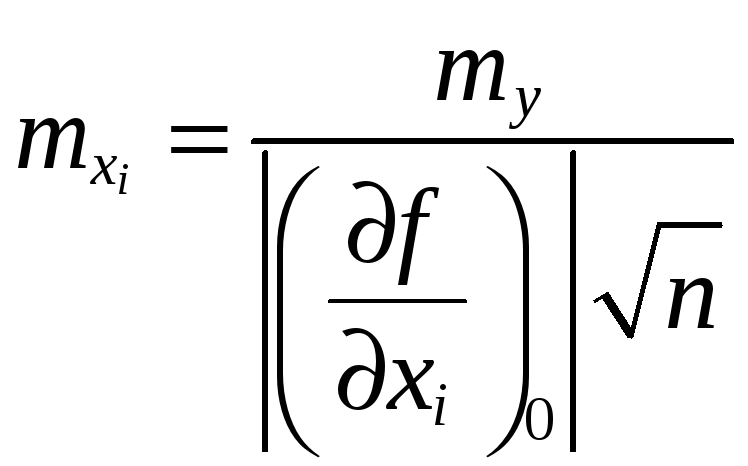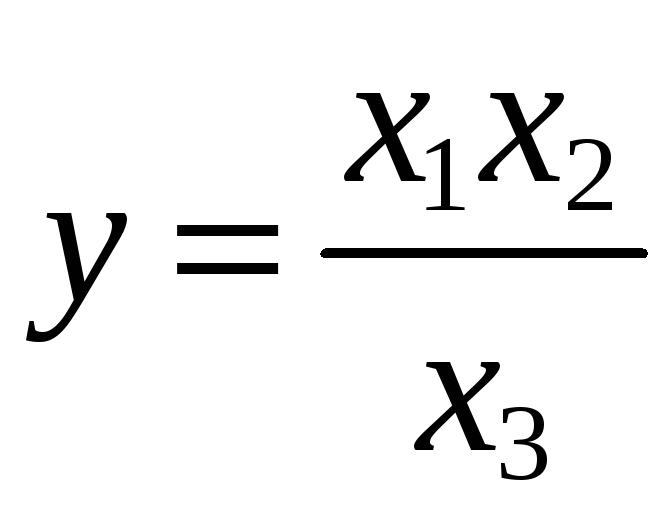