30). Нечеткий вывод на основе правила композиции.

Системы нечеткой логики основаны на нечетких продукционных правилах

А- маленькие

В- большие

Множество чисел Х= Y=

А=

B=

31). Модель нейрона Мак-Каллока и Питтса. Модель формального нейрона.

Нейрон – клетка, которая обрабатывает информацию.

Нейронной сетью называется динамическая система, состоящая из совокупности связанных между собой элементарных процессоров, называемых формальными нейронами.

Формальный нейрон – элементарный процессор, используемый в узлах нейронной сети.

f – функция активации.

32).Модель персептрона Розенблата.

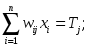
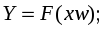
	0	1
0	A	B
1	B	A

Простейшие линейные персептроны реализуют принцип распознавания образа путем получения кластеров путем деления плоскости прямыми линиями. Возникает проблема линейности. Пример:

Линейные персептроны не разрешают проблему линейности, которая делит плоскость на 2 полуплоскости. Двухслойный персептрон:

33) Линейные многослойные нейронные сети

Нейронная сеть – динамическая система, состоящая из совокупности связанных между собой элементарных процессоров, называемых формальными нейронами (элементарный процессор, используемый в узлах нейронной сети).

Многослойные сети могут образовываться каскадами слоев. Выход одного слоя является входом для последующего слоя.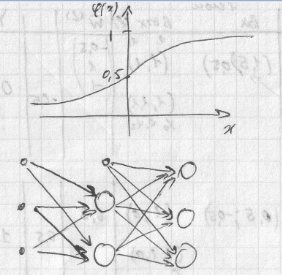

- сигмоида

Из ассоциативного закона умножения матриц следует, что в случае линейных функций активности можно найти однослойный вариант сети, дающий тот же результат, что и многослойный, но при этом нелинейные проблемы не решаются.

34). Радиальные нейронные сети

х1

х2

1

0

0

I

II

y

φ₁

φ₂

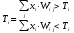
c_i

c_j

x_j

P₁

d_j

Можем разбить на сегменты P.

Сеть с радиальными базисными функциями позволяет решить задачу линейности, то есть разбиения плоскости на сегменты с помощью введения нелинейных сегментов.

Путем введения активной функции φ

Матрица весовых коэффициентов:

1.

x1	x2	φ1	φ2	y
0	0	0,135	1	0
0	1	0,368	0,368	1
1	0	0,368	0,368	1
1	1	1	0,135	0

2.

3.

4.

Решение проблемы линейности

Имеется P областей.

(0,135, 1)

В скрытом слое должно быть P нейронов, соединенных связями W_i

Обобщенная структура радиальной сети рбф

+

+

+

+

+

x₁

x₂

x_N

1

φ₁

φ₂

φ₃

φ_k

W₀

W₁

W₂

W_k

W₃

y

X=(x_1,...,x_N)

Для каждого K должна реализовываться функция

Использование K скрытых нейронов, соединенных связями с весами W_i с выходными линейными нейронами, означает формирование выходных сигналов путем суммирования взвешенных значений соответствующих базисных функций.

Если возьмем следующую матрицу:

,

где определяет радиальную функцию с центром в точке x_i с пришедшим вектором x_j

, где j определяется по числу входных элементов.

d₁

d₂

d_k

...

K