1).Теоретико-множественные операции над расплывчатыми множествами

Нечеткие множества (НМ) предназначены для описания процессов или ситуаций в условиях неопределенности. Они задаются следующим образом:

- универсальное множество.

- нечеткое множество A

- мера принадлежности переменной x множеству A, которая принимает значения от 0 до 1

- носитель нечеткого множества A

Операции над НМ:

1. 

2. 

3. - дополнение до A

4. 

- прямое произведение

5. - альфа-уровень

6. - разность

7. Симметричная разность

2)Расплывчатое включение и расплывчатое равенство множеств

ν – степень включения множества А в В.

ν( ) = &_xєX(μ_A(x) → μ_B(x)), если ν( )≥0.5, то расплывчато является подмножеством В.

Расплывчатые равенства множеств определяются степенью расплывчатости: ν( ) = &_xєX(μ_A(x) ↔μ_B(x)), если А входит в В, и если В входит в А.

Если ν( ) > 0.5, то ≈

Пример1. X = {x₁,x₂,..x₅} = {(0.3;x₂);(0.4;x₄);(0.6;x₅)}

={(0.6;x₁),(0.8;x₂),(0.7;x₄),(0.9;x₅)}

ν( ) = (0→0.6)& (0.3→0.8)& (0.4→0.7)& (0.6→0.9)= (10.6)& (0.70.8)& (0.60.7)& (0.40.9)=1&0.8&0.7&0.9=0.7

μ( )= &_xєX(μ_A(x) → μ_B(x)) &(μ_B(x) → μ_A(x));

μ( )=( )& ()

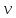Пример2.

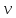()=(0→0.6)&(0.3→0.8)&(0→0)&(0.7→0.4)&(0.9→0.6)=0.4&0.3&1& 0.4&0.6=0.3

5). Расплывчатые высказывания и операции над ними.

Расплывчатым высказыванием называется предложение относительно истины которому можно судить в определенный момент времени.

Импликацией PB и называется высказывание, если то (->), степень истинности определяется выражением:

Эквивалентностью PB и называется степень истинности высказывания

,

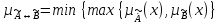Два высказывания называются расплывчато близкими, если мера

Пример:

Определить -?

Решение:

Заключение PB(оценка истинности) требуется в тех случаях, когда либо формулировки задачи, либо формулировки функциональных соответствий между компонентами в условиях задачи существования неопределенности с известными степенями принадлежности.

6) . Расплывчатые логические формулы и их свойства

Под расплывчатой высказанной переменной будем понимать РВ(расплывчатое высказывание) степень истинности, которого, может принимать значение из интервала [0;1].

РЛФ называется любое расплывчатое высказывание, переменная или выражение полученных из расплывчатых логических формул, прим. конечного числа логических операций.

Степень равносильности

При .

Пример

Известно:

Определить:

Формулы и расплывчато близки при заданных значениях мер принадлежности и .

Если мера ,которая касается всех переменных, которые входят в формулу говорят, что эта формула расплывчато истинная ,в противном случае ложная .

Если формула является и формула является , то дизъюнкция является и , конъюнкция является

7) . Сложные нечеткие высказывания

Пусть имеются лингвистические переменные и , определенные на множествах X и Y; их значения , – это нечеткие переменные, которые заданы на множествах:

Могут иметь место выражения вида:

( есть и есть ); ( есть или есть );

( есть и есть ); ( есть или есть );

(если есть , то есть );

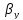(если есть , то есть , иначе )

Конъюнктивная форма

Справедливо выражение

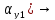есть и есть ((, ) есть )

, – значения лингвистических переменных и , соответствующие множествам:

, – цилиндрические продолжения множеств 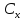и

;

Дизъюнктивная форма

Справедливо выражение

есть или есть ((, ) есть )

;

;

Импликативная форма

есть , то есть ((, ) есть )