30. Поверхности второго порядка.

Поверхностью второго порядка наз множество М точек плоскости, координаты х,у которых удовлетворяют алгебраическому уравнению второй степени.

Цилиндрические поверхности.

Поверхность которая образуется при движении прямой образующей вдоль направляющей линии и при этом образующая остается параллельна оси координат наз цилиндрической. В зависимости от вида направляющей линии цилиндр поверхности подразделяются на 3 вида:

1. эллиптический цилиндр (напр линией явл эллипс)

х²/а²+у²/в²=1 – уравнение эллиптического цилиндра.

Напр линия- эллипс в плоскости ХОУ

Образующая параллельна ОZ

2. гиперболический цилиндр- направляющей явл гипербола

х²/а²-у²/в²=1, образующая параллельна ОZ

3. параболический цилиндр – напр явл парабола

у²= 2рх или х²= 2ру, направляющая параллельна ОZ

общие поверхности второго порядка

1. сфера х²+у²+z²=R²

2. трехконусный эллипсоид х²/а²+у²/в²+z²/c²=1

3. однополосный гиперболоид х²/а²+у²/в²-z²/c²=1

4. . двухполосный гиперболоид х²/а²+у²/в²-z²/c²=-1

5. конус х²/а²-у²/в²-z²/c²=0

6. эллиптический параболоид х²/а²+у²/в²=z

7. гиперболический параболоид х²/а²-у²/в²=z

Если центр или вершина поверхности нах не в начале координат, ам в точке М, то уравнение таких поверхностей получается из приведенных выше уравнений заменами:

х—(х-х´)

у—(у-у´)

Если поверхность задана общим уравнением вида Ах²+Ву²+Сху+Дх+Еу+Fz+М=0, то для определения вида поверхности и ее параметров данное уравнение необходимо привести к каноническому виду с помощью метода выделения полных квадратов.

Определение и геометрический смысл производной

Пусть функция f(x) непрерывна в точке .

Определение. Производной от функции в точке называется величина

Дадим некоторые расшифровки этого важнейшего понятия математического анализа.

а) Вспоминая определение предела можно записать определение через кванторы .

б) Величина называется приращением аргумента, а величина приращением функции. Тогда

в) Обозначая , можно записать

Понятие производной впервые появилось в физике в связи с понятием скорости. Пусть некоторая материальная точка движется по оси так что есть координата точки в момент времени. Спустя время dt координата точки будет , т.е. за время точка пройдет путь . Поэтому средняя скорость точки за интервал времени будет равна. Чтобы найти мгновенную скорость точки в момент времени надо устремить кнулю, т.е.

Таким образом, производная от координаты точки определяет ее мгновенную скорость. Поэтому и производную функции в некоторой точке можно трактовать как скорость изменения функции.

Дадим еще геометрический смысл производной. В определение производной входят две операции: деление и предельный переход при . Что же это дает?

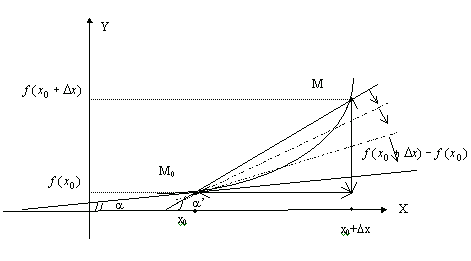
Нанося на график точки с координатами (, ) и (, ) мы получим фигуру изображенную на рисунке. Проведем через эти точки линию, которая называется секущей. Тогда дробь есть не что иное как , где есть угол наклона секущей к оси OX.

Но, в определении производной есть еще предельный переход при . Что же дает этот предельный переход?.

При точка M начинает двигаться к точке M₀. При этом вся секущая будет поворачиваться около точки M₀ и в пределе она превратиться в касательную к точке M₀. Угол при этом перейдет в угол , который эта касательная образует с осью OX. Поэтому можно утверждать, что

где угол, образованный касательной к кривой в точке и осью OX.