Лекція 15 Релаксаційні коливання в лазерах

Релаксаційні коливання інтенсивності спостерігаються в більшості лазерів. Характерний період таких коливань значно перевищує час життя фотону в резонаторі і час обходу резонатора . Найчастіше цей період знаходиться в інтервалі мкс. Основним фізичним механізмом релаксаційних коливань є взаємодія генеруючого поля в резонаторі з активним середовищем. Зростання інтенсивності поля викликає зменшення інверсії населеностей внаслідок того, що збільшується ймовірність вимушених переходів. Це, в свою чергу, означає зменшення підсилення і приводить до зменшення інтенсивності поля випромінювання. При побудові математичної моделі цього явища будемо виходити з ідеалізованої моделі лазера з однорідно розширеним контуром підсилення. Допустимо також, що населеність нижнього лазерного рівня дуже мала, тобто виконується умова , і будемо рахувати густину інверсії Швидкість накачування на рівень 2 (атомів/м³с) рівна , а час розпаду стану 2 під дією любих причин, крім вимушеного випромінювання, рівний .Позначивши через ймовірність індукованого переходу на один атом, запишемо рівняння:

(15.1)

Ймовірність пропорційна інтенсивності поля а значить, і густині фотонів в резонаторі. Тому рівняння (15.1) можна переписати наступним чином:

(15.2)

де – коефіцієнт, який визначається співвідношенням: Оскільки це одночасно і ймовірність випромінювання фотону, маємо також рівняння:

(15.3)

Рівняння (15.2) і (15.3) описують взаємодію між полем випромінювання з густиною фотонів і активним середовищем з густиною інверсії По своїй суті отримали нелінійну систему диференціальних рівнянь, які неможливо розв’язати точно аналітично. Розв’язок можна отримати лише числовими методами. Перш за все зауважимо, що в стаціонарному режимі і справедливі співвідношення:

(15.4)

З (15.4) випливає, що при густина фотонів Позначимо це порогове значення накачування через і введемо фактор перевищення порогу що дозволяє записати друге із співвідношення (15.4) у вигляді

(15.5)

0

Розглянемо тепер поведінку системи при малому відхиленні від рівноваги, задавши Підставивши ці вирази у рівняння (15.2) і (15.3), використовуючи (15.4) і нехтуючи малими нелінійними членами типу (лінеаризаця рівнянь, допускаючи, що розв’язки дуже близькі до стаціонарного розв’язку), отримаємо:

(15.6)

(15.7)

Взявши похідну від (15.7), і підставивши в отриману рівність з (15.6) та використавши (15.4), приходимо до

(15.8)

або оперуючи фактором перевищення порога отримаємо:

(15.9)

Ми отримали рівняння гармонічного осцилятора з втратами. Запропонувавши його розв’язок у вигляді приходимо до характеристичного рівняння

яке має корені причому:

(15.10)

Отже, розв’язок лінеаризованого рівняння (15.9) має вигляд Вихідна потужність (вона пропорційна числу фотонів в резонаторі) має синусоїдальні затухання коливань з частотою і декрементом які зростають із збільшенням потужності накачування.

Передбачені теорією затухаючі гармонічні коливання інтенсивності, дійсно, спостерігаються у деяких лазерів, але часто коливання виявляються незатухаючими. Режим першого типу властивий лазеру на CaWO₄:Nd³⁺.

Приклад. Релаксаційні коливання. Задамо наступні значення параметрів лазера: с, c, і розрахуємо за формулою (15.10), отримаємо: с.

На рис. 15.1а представлені залежності зміни в часі і , якщо дані відповідають вище наведеному прикладу, а Ці графіки побудовані на основі числового розв’язку рівнянь (15.2) і (15.3) з врахуванням виразів (15.4) і (15.5) Такі залежності є типовими для твердотільних лазерів. Навіть незначне відхилення від і від рівноважних положень приводить до сильних осциляцій у величині тобто вихідної потужності, проте мало відхиляється від положення рівноваги. Випромінювання має пічкову структуру, що спостерігається для реальних лазерів. Якщо співмірне з часом життя фотонів в резонаторі (характерно для газових лазерів), то осциляції практично відсутні, і потужність випромінювання лазера досить швидко виходять на стаціонарний рівень, що демонструє рис.15.1б. Для даного випадку

Рис.15.1. Залежність інверсної населеності і густини фотонів в резонаторі в часі.

Дуже часто незатухаючі пульсації інтенсивності випромінювання лазерів, які спостерігаються можна пояснити, по крайні мірі, якісно, розглядаючи рівняння (15.9) . Воно, як відомо, співпадає по формі з рівнянням осцилятора без зовнішньої дії або RCL–контура. Незатухаючі коливання такого осцилятора виникають під дією зовнішньої сили. Одним із механізмів вимушеного розкачування пульсацій може бути швидкість накачування яка змінюється з часом. В даному випадку представимо накачування у вигляді

(15.11)

Відтворюючи виведення рівняння (15.6) і маючи на увазі рівняння (15.11) приходимо до видозміненого рівняння для інверсії . Тоді замість (15.9) отримаємо

(15.12)

Здійснивши фур’є-перетворення обох частин останнього рівняння, позначивши фур’є-образи величин i через і , відповідно, знаходимо

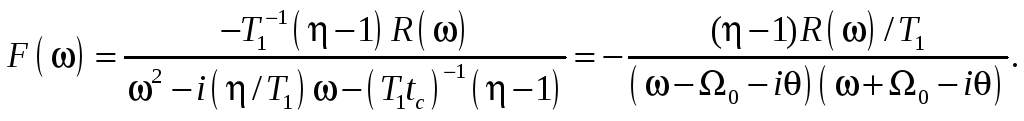(15.13)

Зауважимо, що і співпадають з частотою та декрементом затухання перехідних пульсацій, які подаються формулами (15.10). Якщо припустити, що спектр вимушуючої сили однорідний (тобто подібний до спектру ”білого шуму”) поблизу частоти , то фур’є-спектр буде мати пік з вершиною на частоті і з шириною Крім того, якщо то можна очікувати, що в часовому представленні флуктуації інтенсивності будуть промодульовані з частотою

Зроблені висновки підтверджуються експериментальними результатами, які відносяться до лазерів різних типів. Резонансна природа відгуку проявляється також і в дослідах з модуляцією яких-небудь параметрів лазера на частотах близьких до . Внутрішня модуляція зв’язку на цих частотах звичайно відбувається у випромінюванні з сильними спотворення.