Розділ 5 лазер. Режим генерації

Пропозиція про використання вимушеного випромінювання в системах з інверсною населеністю для підсилення НВЧ сигналів були висловлені незалежно Вебером, Гордоном, Таунсом, Басовим і Прохоровим. Середовище з інвертованою населеністю рівнів може підсилювати випромінювання на частотах поблизу атомного переходу. В цьому розділі ми розглянемо процеси, що протікають в середині оптичного резонатора, заповненого активним середовищем. Слабі флуктуаційні поля мод в цьому випадку будуть підсилюватися. Для деяких мод з найменшими втратами (висока добротність Q) підсилення може перевищити втрати. Ці моді будуть наростати по інтенсивності до того часу, поки ефект насичення не обмежить підсилення на рівні втрат і не встановиться стаціонарна генерація. В цьому ж розділі будуть розглядатися режими роботи лазера

Лекція 13 Виникнення генерації

13.1 Умови генерації.

Найдемо умови генерації лазера, тобто визначимо густину інверсної заселеності рівнів активного середовища, яка відповідає порогу генерації, і частоту, на якій випромінює лазер. Для того, щоб краще зрозуміти природу генерації, можливо, виведемо умову генерації двома незалежними способами.

В цій лекції викладається перший підхід, який ґрунтується на законіABCD. Умова генерації випливає з вимоги відтворення пучка, його амплітуди і фази після кожного повного обходу резонатора. Для опису пучка зручно ввести функцію

. (13.1)

Параметр є комплексним параметром пучка і визначається співвідношенням

(13.2)

а множник – комплексна амплітуда хвилі в точці . Комплексну величину представимо у вигляді , так що інтенсивність поля в точці відноситься до інтенсивності в точці як , а відповідна зміна фази стає рівною – .

Проходження гаусового пучка через деякий оптичний елемент, що відмічений індексом , описується рівнянням:

, (13.3)

яке перетворюється до виду:

, (13.4)

де – коефіцієнт перетворення комплексної амплітуди, що здійснюється –елементом. Оптичний елемент тепер характеризується матрицею ABCD і крім цього коефіцієнтом перетворення . З попередніх лекцій відомо, що для шару однорідного середовища, яке може підсилювати або поглинати електромагнітну хвилю, і яке обмежене площинами і :

. (13.5)

Тут – комплексна постійна поширення, яка враховує зміну фази і зміну амплітуди в результаті затухання чи підсилення хвилі. Сферичне дзеркало, матриця ABCD якого приведена в попередніх лекціях, має коефіцієнт перетворення , де – коефіцієнт відбивання по потужності, – фазовий зсув, що виникає при відбиванні.

Результат послідовного проходження гаусового пучка через оптичних елементів можна представити в наступній формі:

, (13.6)

де ABCD – елементи добутку декількох A_sB_sС_sD_s – матриць, – фаза коливань при проходженні тих же елементів.

Застосуємо цей формалізм до виведення умови генерації лазера. Розглянемо резонатор, який зображений на рис. 13.1.

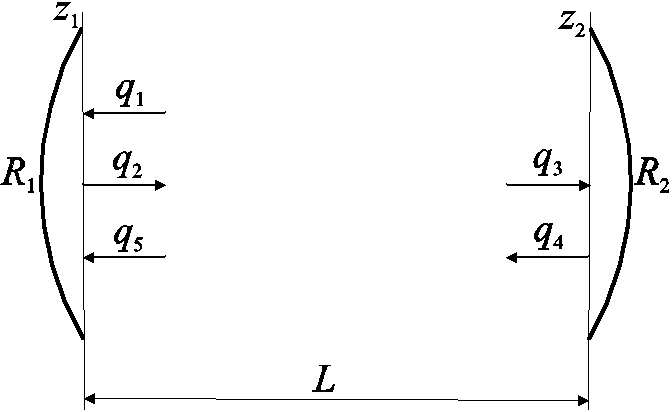
Рис.13.1 Поширення гаусового пучка з комплексним параметром в прямому і зворотному напрямах в резонаторі, заповненого активним середовищем,

Він складається з двох дзеркал з коефіцієнтами відбивання по амплітуді i відповідно. Резонатор заповнений підсилювальним середовищем, яке характеризується комплексною постійною поширення Прослідкувавши еволюцію гаусового пучка за один прохід резонатора, будемо мати:

(13.7)

Використовуючи (13.5) і (16.6), вважаючи, що отримаємо:

. (13.8)

Будемо вимагати, щоб форма пучка, а також його комплексна амплітуда відновлювалась після кожного обходу резонатора. Це буде тоді коли:

(13.9)

де – ціле число. Перша умова виконується у випадку Друга умова задовольняється тоді, коли або з врахуванням (13.8):

(13.10)

Це і є умова генерації лазера, яка відповідає інтуїтивному уявленню про те, що в стаціонарному режимі генерації амплітуда і фаза поля приймають одні і ті ж значення після кожного проходу пучка по резонатору. Ця обставина буде використана нижче для визначення порогової густини інверсії, а також частоти генерації.