4. Показникова функція.

Показникова (експоненціальна) функція комплексної змінної визначається рівністю

.

На дійсній осі ця функція збігається з дійсною експонентою .

Зберігаються основні правила: 1); 2) ; 3) .

Оскільки , то

– формули переходу

Похідна комплексної експоненти дорівнює їй самій і всюди відмінна від нуля . Тому ця функція аналітична у всій комплексній площині і задає конформне відображення. При цьому довільна горизонтальна пряма перетворюється у відкритий промінь, що виходить з початку координат, а довільний вертикальний відрізок довжиною переходить в коло з центром у початку координат.

Зауваження. Функція є періодичною з уявним періодом .

Справді, .

Через періодичність комплексної експоненти відображення буде однолистим у кожній горизонтальній смузі

, де .

Кожна така смуга відображається в -площину з вилученим початком координат (рис. 2). При цьому координатна сітка декартової системи на -площині перетворюється в сітку полярних координат на -площині.

П риклад 1. Знайти образ множини при відображенні .

Розв’язування. Оскільки для множини маємо

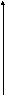
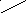
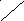
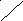
5. Тригонометричні та гіперболічні функції.

Тригонометричні та гіперболічні функції комплексного аргументу визначаються за основної формули Ейлера

і узагальнюють відповідні дійсні функції:

; ;

; ; .

Оскільки комплексна експонента є періодичною з уявним періодом , то тригонометричні функції і також періодичні на всій комплексній площині з дійсним періодом , а і – з дійсним періодом :

; ;

; .

Причому на відміну від дійсних функцій, на всій комплексній площині і є необмеженими:

, при .

Гіперболічні функції і на всій комплексній площині є періодичними з уявним періодом , а і – з уявним періодом :

; ;

; .

Комплексні тригонометричні функції і приймають нульові значення тільки в точках дійсної осі, в яких відповідно і . Аналогічно, комплексні гіперболічні функції і приймають нульові значення тільки в точках уявної осі, в яких відповідні тригонометричні функції перетворюються в нуль: і .

Зауваження 1. Для тригонометричних і гіперболічних функцій комплексного аргументу залишаються справедливими основні тотожності (синус и косинус суми, різниці та ін.), а також формули диференціювання.

Допоміжні формули Ейлера

; ; ;

дають зв’язок гіперболічних функцій з тригонометричними.

Зауваження 2. Геометрично зв’язок гіперболічних функцій з тригонометричними зводиться до поворотів на образів і прообразів.

Зауваження 3. При комплексних аргументах зникають принципові відмінності між показниковою, тригонометричними і гіперболічними функціями: експонента стає періодичною, і – необмеженими і т.п. Формули Ейлера відображають тісний внутрішній зв’язок цих функцій: їх можна розглядати як різні прояви одних і тих же закономірностей.

Приклад 1. Знайти .

Розв’язання.

.