3. Ряд Лорана.

Розглянемо узагальнений степеневий ряд

,

де – коефіцієнти ряду, – центр ряду.

Цей ряд містить як невід’ємні, так і від’ємні степені різниці . Частина ряду, яка містить доданки, що прямують до коли називається головною частиною ряду, а решта –правильною. Отже, в нашому випадку головна частина ряду, а – правильна. Узагальнений степеневий ряд збігається, якщо одночасно збігаються його головна і правильна чистини. Правильна частина як звичайний степеневий ряд збігається всередині деякого круга з центром і радіусом . Якщо у головній частині зробити заміну , то отриманий звичайний степеневий ряд збігається всередині деякого круга з центром і радіусом . Нехай . Повертаючись до змінної , можна встановити, що головна частина збігається зовні круга з центром і радіусом .

Якщо області і мають непорожній переріз, то узагальнений степеневий ряд збігається у їх спільній частині – кільці (рис. 2). На межі кільця ряд може як збігатися, так і розбігатися.

Приклад 1. Знайти область збіжності узагальненого степеневого ряду

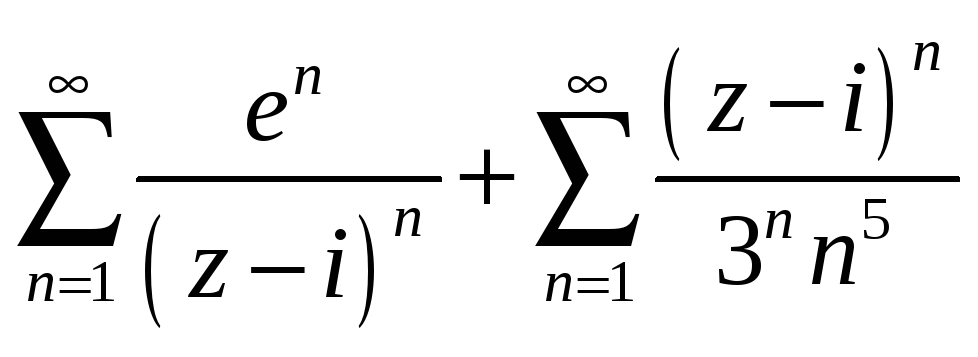
Розв’язання. Знайдемо область збіжності головної частини . Застосовуючи радикальну ознаку Коші до ряду з модулів, визначаємо радіус збіжності

.

Тобто, головна частина абсолютно збігається при . На колі цей ряд розбігається, оскільки для відповідного ряду не виконується необхідна ознака збіжності.

Знайдемо область збіжності правильної частини . Застосовуючи ознаку Даламбера до ряду з модулів, визначаємо радіус збіжності

.

Тобто, правильна частина абсолютно збігається при . На колі цей ряд теж абсолютно збігається, оскільки відповідний ряд з модулів є збіжним узагальненим гармонічним рядом. Тоді областю збіжності правильної частини служить замкнений круг .

Отже, областю збіжності початкового сумарного ряду служить спільна частина знайдених областей – кільце з центром .

Нехай функція аналітична в деякій області за винятком окремих особливих точок. Візьмемо довільну точку цієї області. Якщо точка – правильна, то функцію можна розвинути в ряд Тейлора, радіус збіжності якого дорівнює відстані від центра до найближчої особливої точки. Якщо точка – особлива, то функцію не можна розкласти в ряд Тейлора за степенями .

Проведемо концентричні кола з центром через кожну особливу точку області . Тоді всередині кожного кільця між сусідніми колами особливих точок не буде. Наступна теорема дає розв’язок задачі: розкласти функцію , що аналітична в кільці , в узагальнений степеневий ряд.

Теорема 1 (теорема Лорана). Нехай функція – аналітична в круговому кільці з центром у точці . Тоді вона може бути однозначно подана у цьому кільці збіжним узагальненим степеневим рядом Лорана

;

,

де – довільне коло .

Зауваження 1. Збіжний в деякому кільці до функції ряд Лорана можна почленно диференціювати та інтегрувати. Отримані при цьому ряди збіжні у тому ж кільці.

Зауваження 2. Ряд Тейлора є окремим випадком ряду Лорана, коли в останньому відсутня головна частина (, ).

Зауваження 3. Нехай функція аналітична в круговому кільці – в проколотому околі нескінченно віддаленої точки . Якщо перейти до нової змінної , то одержана функція аналітична в кільці – в проколотому околі точки . Розкладаючи функцію в ряд Лорана в околі точки і повертаючись до змінної , можна отримати ряд Лорана за степенями функції в околі нескінченно віддаленої точки :

; ,

де – головна частина; – правильна частина (зміст і назви частин ряду протилежні тим, що мають місце для ряду Лорана з центром у скінченній точці).

Зауваження 4. Нехай функція – аналітична в круговому кільці і обмежена, тобто існує таке число , що в даному кільці. Тоді коефіцієнти ряду Лорана задовольняють нерівності Коші

,

де , , .

Теорема (Ліувілля). Якщо функція аналітична в і обмежена, то

Приклад 2. Розкласти в ряд за степенями функцію

.

а) у крузі (в околі точки );

б) у кільці ;

в) у кільці (в околі нескінченно віддаленої точки ).

Розв’язання. Особливими точками даної функції є точки і (у цих точках знаменник дорівнює нулю). Тому існують три області з центром у правильній точці (рис. 3), де функція є аналітичною і може бути розвинена в ряд за степенями :

а) у крузі – в ряд Тейлора; б) у кільці – в ряд Лорана; в) у кільці – в ряд Лорана.

Оскільки дана функція є правильним раціональним дробом, то: 1) розкладемо її на суму елементарних дробів; 2) у відповідній області кожен з доданків перетворимо до вигляду суми нескінченно спадної геометричної прогресії і перейдемо до відповідної прогресії; 3) підставляючи отримані розклади у вираз для функції , знайдемо шукане розвинення цієї функції в ряд Лорана у відповідній області.

.

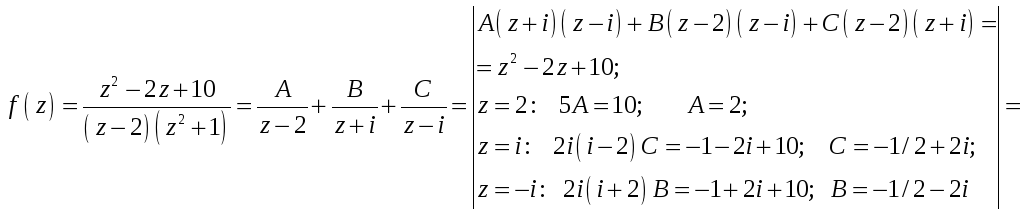
а) у крузі :

;

;

;

.

б) у кільці :

(для першого доданку використовуємо знайдене в пункті а) розвинення);

;

в) у кільці :

.

Для другого і третього доданків використовуємо знайдені в пункті б) розвинення:

;

.

Тоді

Приклад 3. Розкласти в ряд Лорана функцію

в (проколотому) околі точки .

Розв’язання. Особливими точками даної функції є точки і (див. попередній прикл. 2). Тому існують дві області з центром в особливій точці (рис. 4), де функція є аналітичною і може бути розвинена в ряд за степенями різниці :

а) у кільці (у проколотому околі точки ) – в ряд Лорана;

б) у кільці – в ряд Лорана.

У поставленій задачі розглядається (проколотий) окіл точки . Радіус визначається як відстань від центра до найближчої особливої точки (в даному випадку обидві особливі точки розміщені на однаковій відстані від точки ).

Розкладемо функцію на суму елементарних дробів (див. попередній прикл. 2):

.

Перший доданок виражений через степінь різниці , тобто має потрібний вигляд. Другий і третій доданки перетворимо до вигляду суми нескінченно спадної геометричної прогресії відносно різниці і перейдемо до відпо­відної прогресії. Підставляючи отримані розклади у вираз для функції , знайдемо розвинення цієї функції в ряд Лорана в (проколотому) околі точки :

;

;

.

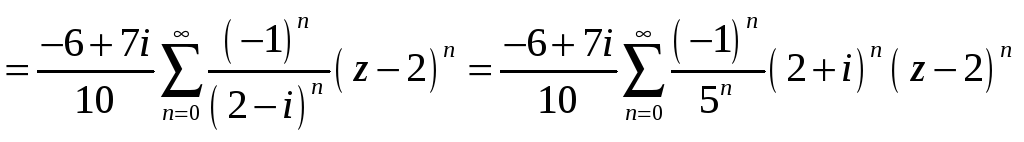Лекція 11.